Java中的常量和常量的表现形式及进制的转换
Posted 想一千次不如去做一次,华丽的跌倒,胜过无谓的徘徊...
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Java中的常量和常量的表现形式及进制的转换相关的知识,希望对你有一定的参考价值。
1.常量
在程序执行的过程中,其值不发生改变的量。
分类:
(1) 字面值常量
字符串常量:用双引号括起来内容
字符常量:用单引号括起来的内容
整数常量:所有整数
小数常量:所有小数
布尔常量:true 或 false
空常量: null
(2) 自定义常量(符号常量)
用final修饰变量(也就是常量)
2.常量的表现形式
Java针对整数常量提供了4种表现形式:
二进制 八进制 十进制 十六进制
3.进制的概述:
进制就是进位制,是人们规定的一种进位方法。几进制就是逢几进一。
计算机的电子原件的状态只有开和关两种,分别用1和0来表示。
如果我们表达数据只用这两种状态,那么能够表达的数据是比较少的。
我们常见的数据:英文字母,数字,标点,符号……有很多,两个状态
肯定是不够的。
为了能够表达更多的数据,国际化标准组织就规定:用8个这样的信号表示
一个数据,这个数据的单位叫:字节(byte);
不同进制的组成:
二进制:由0,1组成,以 0b 开头。
八进制:由0,1,2,... 7组成,以 0 开头。
十进制:由0,1,2,...9组成,默认为十进制数。
十六进制:由0,1,2,...a,b,c,d,e,f(大小写均可) 组成,以0x开头。
4.进制间的转换
其它进制到十进制的转换:位权展开法。
由十进制 ➡ 十进制推理:
十进制数 12345 = 10000 + 2000 + 300 + 40 + 5
= 1*10^4 + 2 *10^3 + 3*10^2 + 4*10^1 + 5*10^0
= 10000 + 2000 + 300 + 40 + 5
=12345
二进制 ➡ 十进制:
二进制数 100 = 1*2^2 + 0*2^1 + 0*2^0
=4 + 0 + 0
= 4
八进制 ➡ 十进制:
八进制 100 = 1*8^2 + 0*8^1 + 0*8^0
= 64 + 0 + 0
= 64
十六进制 ➡ 十进制:
十六进制 100 = 1*16^2 + 0*16^1 + 0*16^0
= 256 + 0 + 0
= 256
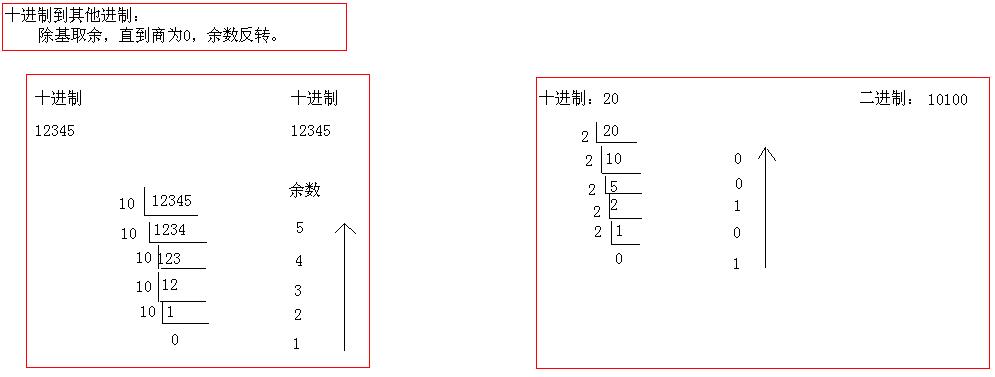
十进制到其它进制:转几进制,就除几,余数倒着取。八进制和十六进制同理。
十进制和二进制的快速转换法:8421码
它表达的意思是每一个二进制位上的数据对应一个固定的值。
只需要把对应的1位置的数据值相加,即可得到该二进制对应的十进制的值。
二进制: 1 1 1 1 1 1 1 1
十进制:128 64 32 16 8 4 2 1
Eg:二进制1010100转十进制:
0b1010100 = 64 + 16 + 4
= 84
十进制100转二进制:
100 = 0b1100100
二进制到八进制,十六进制
(1)先转成十进制,再转成其他进制
(2)拆分组合法
二转八进制:
把二进制的数据从右开始,每三位一组合,最左边不够用0补齐,然后
分别计算出对应的十进制数值,最后把每个十进制的数据组合起来,就是
一个八进制数据。
二转十六:
把二进制的数据从右开始,每四位一组合,最左边不够用0补齐,然后
分别计算出对应的十进制数值,最后把每个十进制的数据组合起来,就是
一个十六进制数据。
进制越大,表现形式越短。
5.有符号数据表示法:
在计算机内,有符号数有3中表示法:原码,反码和补码。
所有数据的运算都是采用补码进行的。
原码:
就是二进制定点表示法,即最高位为符号位,"0" 表示正 "1"表示负,其余位表示数据的大小。
反码:
正数的反码与其原码相同;负数的反码是对其原码逐位取反(1变0,0变1),符号位除外。
补码:
正数的补码与其原码相同;负数的补码是在其反码的末位加1。
总结:正数的原码,反码,补码相等。
以上是关于Java中的常量和常量的表现形式及进制的转换的主要内容,如果未能解决你的问题,请参考以下文章