本题是比较典型的滑动窗口问题
这类问题一般通过一个滑动窗口就能在O(N)的时间复杂度下求解
本题可以先退化成考虑K=0的情况,此时题目就变成了求解字符串中最长连续子串长度问题了
我们先可以通过这个特例先了解一下滑动窗口的求解过程
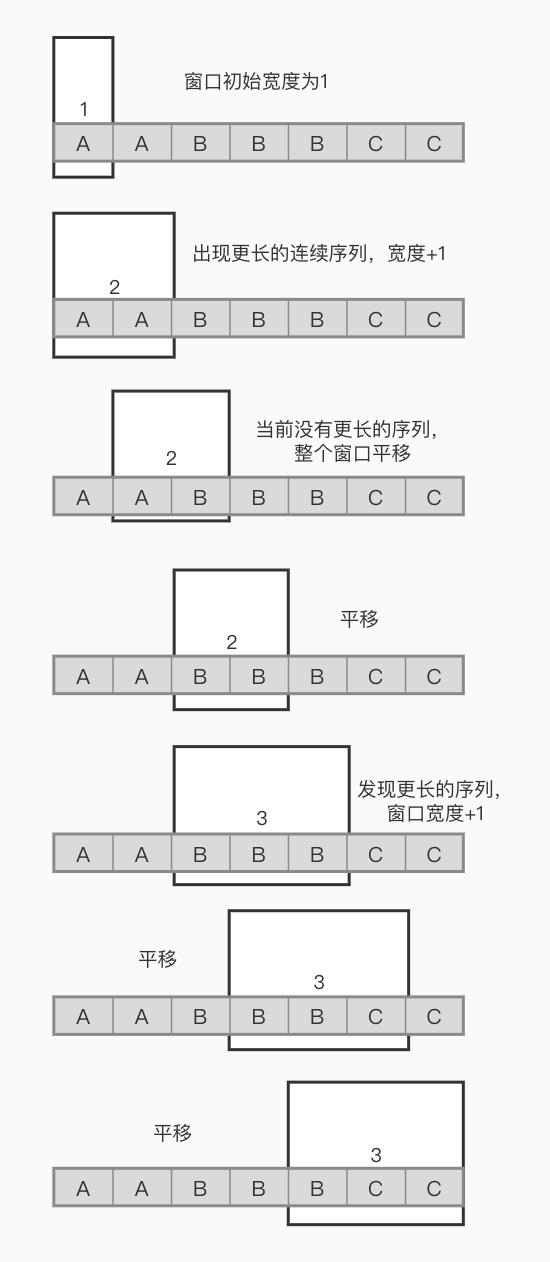
上图的求解过程展示中,窗口从左至右不断扩张/滑动,当窗口触达字符串末尾字符时,运算结束,窗口的宽度为最终结果。初始窗口的宽度为1,我们不断的通过向当前窗口覆盖的子串后面追加一个字符看是否能满足我们的要求,如果满足窗口扩张,如果不满足,窗口向右滑动。
当K>0时,子串的条件变成了允许我们变换子串中的K个字符使其变成一个连续子串
那么这个题的关键点就是我们如何判断一个字符串改变K个字符,能够变成一个连续串
如果当前字符串中的出现次数最多的字母个数+K大于串长度,那么这个串就是满足条件的
我们维护一个数组int[26]来存储当前窗口中各个字母的出现次数,left表示窗口的左边界,right表示窗口右边界
- 窗口扩张:left不变,right++
- 窗口滑动:left++, right++
charMax保存滑动窗口内相同字母出现次数的历史最大值,通过判断窗口宽度(right - left + 1)是否大于charMax + K来决定窗口是否做滑动,否则窗口就扩张
完整Java代码
class Solution {
private int[] map = new int[26];
public int characterReplacement(String s, int k) {
if (s == null) {
return 0;
}
char[] chars = s.toCharArray();
int left = 0;
int right = 0;
int charMax = 0;
for (right = 0; right < chars.length; right++) {
int index = chars[right] - \'A\';
map[index]++;
charMax = Math.max(charMax, map[index]);
if (right - left + 1 > charMax + k) {
map[chars[left] - \'A\']--;
left++;
}
}
return chars.length - left;
}
}