SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS 论文/GCN学习笔记

Posted 2023-02-22 Dodo·D·Caster

1 前置知识：卷积与CNN

该内容在论文中并没有涉及，但理解卷积和CNN对于GCN的理解有帮助，因为GCN是将CNN推广到新的数据结构：graph上面。

1.1与1.2的内容均来自视频：https://www.bilibili.com/video/BV1VV411478E/?spm_id_from=333.880.my_history.page.click&vd_source=9e34c29511733195fced9735e60f8683

1.1 卷积

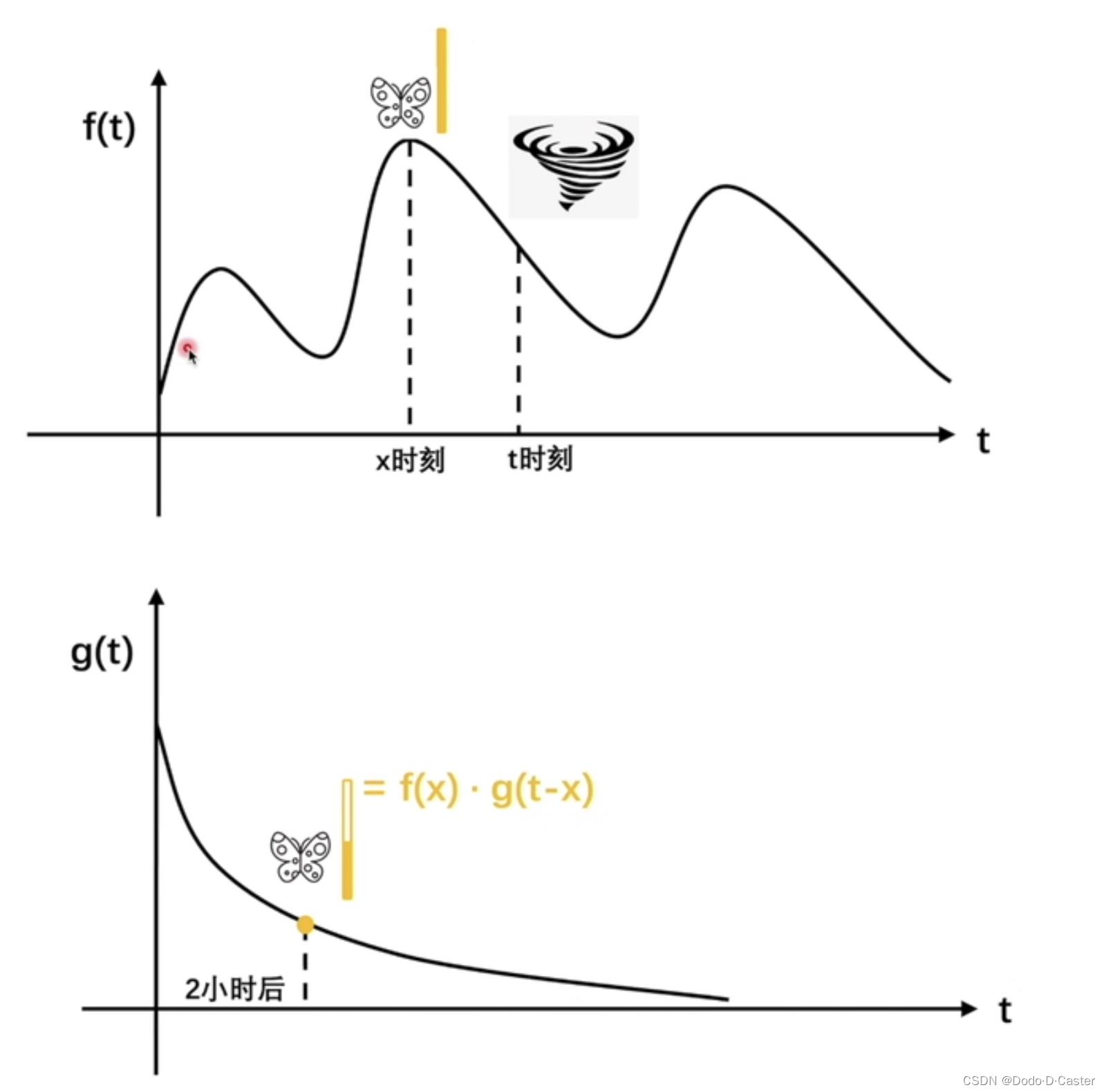
卷积公式：${\int }_0^{t}f(x)g(t-x)dx$

$f(x)$：在每一个时刻$x$，都有$f(x)$个蝴蝶煽动翅膀，如3

$g(y)$：在一个蝴蝶煽动翅膀后，$y$时刻后，该蝴蝶煽动翅膀对引起飓风对影响为$g(y)$，如0.5

则在$x$时刻的3只蝴蝶，经过了$y$时刻，对$x+y$时刻引起飓风的影响为$3\times 0.5=1.5$

假设t时刻发生了飓风，求 $0～t$ 时刻蝴蝶煽动翅膀对飓风的影响，则有公式：${\int }_0^{t}f(x)g(t-x)dx$y由此我们可以得到该问题中卷积的本质：累加过去对现在的影响

1.2 CNN

选取不同的卷积核，用卷积核乘3*3的像素矩阵做卷积，可以得到新的像素点，对图中所有的像素矩阵乘卷积核则可以得到新的图像。

其本质是：累加3*3个像素对目标像素的影响，得到目标像素。

1.3 CNN→GCN

由于graph不同于image，没有固定的结构，邻居的数量亦不相同，故将CNN推广到graph上时，GCN将对像素的卷积操作变成了对节点邻居的卷积操作，累加不同邻居对目标节点的影响，得到新的特征。

2 GCN的数学理论

2.1 图谱卷积公式（K阶近似）

graph上的谱卷积公式：

$$g_{\theta }\star x=U{g}_{\theta }{U}^{T}x$$

• $g_{\theta }$：过滤器，可以理解为对特征值的函数
• $x$：信号，可以理解为每个节点的特征信息
• $L=I_N-D^{-\frac{1}{2}}A{D}^{-\frac{1}{2}}=U\Lambda U^T$
  • $L$：标准化的图拉普拉斯矩阵
  • $\Lambda$ ：特征值矩阵
  • $U^{T}x$：对$x$进行图傅里叶变换

由于上式特征矩阵的乘法复杂度为$O(N^2)$，并且对于large graph是$L$进行特征分解同样在计算上消耗巨大，所以要对$g_{\theta }(\Lambda )$用切比雪夫多项式（Chebyshev polynomials）进行K阶近似：

$$g_{{\theta }^{\prime }}(\Lambda )\approx \sum _{k=0}^K{\theta }_k^{\prime }{T}_k(\tilde{\Lambda })$$

• $\tilde{\Lambda }=\frac{2}{{\lambda }_{max}}\Lambda -I_N$
  • ${\lambda }_{max}$：代表图拉普拉斯矩阵的最大特征值
• ${\theta }^{\prime }$：切比雪夫系数向量
• $T_k(x)=2x{T}_{k-1}(x)-T_{k-2}(x),T_0(x)=1,T_1(x)=x$：切比雪夫多项式的递归定义

结合两个式子，得到总的谱图公式（复杂度为$O(|\mathcal{E}|)$，其中$\mathcal{E}$为边的数量）：

$$g_{\theta }\star x\approx \sum _{k=0}^K{\theta }_k^{\prime }{T}_k(\tilde{L})x$$

• $\tilde{L}=\frac{2}{{\lambda }_{max}}L-I_N$

2.2 Layer-wise线性模型

设定参数：

• $K=1$：也就是切比雪夫采用1阶近似，此时我们可以得到一个线性的公式
• ${\lambda }_{max}\approx 2$：神经网络的参数会在训练的过程中适应这个改变。

这样，我们可以得到简化后的一阶近似线性公式：

g θ ⋆ x ≈ θ 0 ′ x + θ 1 ′ ( L − I N ) x = θ 0 ′ x − θ 1 ′ D − 1 2 A D − 1 2 x g_\\theta \\star x ≈ \\theta_0'x + \\theta_1'(L-I_N)x = \\theta_0'x - \\theta_1'D^-\\frac12AD^-\\frac12x g使用聚类算法进行标签传播学习（Clustering for Semi-Supervised Learning）

Graph-based Semi-Supervised Classification简单总结回顾

论文笔记之：Large Scale Distributed Semi-Supervised Learning Using Streaming Approximation

Deeper Insights into Graph Convolutional Networks for Semi-Supervised Learning

论文笔记：SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS

论文笔记：SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS