Java数据结构和算法树的基本操作

Posted 2021-01-26 binarylei

Java数据结构和算法（二）树的基本操作

一、树的遍历

二叉树遍历分为：前序遍历、中序遍历、后序遍历。即父结点的访问顺序

1.1 前序遍历

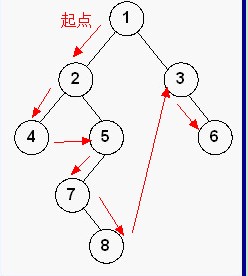
基本思想：先访问根结点，再先序遍历左子树，最后再先序遍历右子树即根—左—右。图中前序遍历结果是：1，2，4，5，7，8，3，6。

// 递归实现前序遍历
public void preOrder() {
    System.out.printf("%s ", value);
    if (left != null) {
        left.preOrder1();
    }
    if (right != null) {
        right.preOrder1();
    }
}

// 非递归实现前序遍历
public void preOrder1() {
    TreeNode<E> head = this;
    Stack<TreeNode<E>> stack = new Stack();
    stack.push(head);
    while (!stack.isEmpty()) {
        TreeNode<E> pop = stack.pop();
        System.out.printf("%s ", head.value);
        if (pop.right != null) {
            stack.push(pop.right);
        }
        if (pop.left != null) {
            stack.push(pop.left);
        }
    }
}

1.2 中序遍历

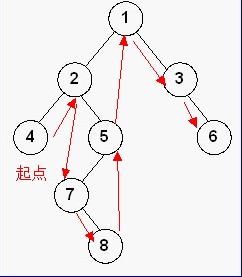
// 递归实现中序遍历
public void midOrder() {
    if (left != null) {
        left.preOrder1();
    }
    System.out.printf("%s ", value);
    if (right != null) {
        right.preOrder1();
    }
}

// 非递归实现中序遍历
public void midOrder1() {
    TreeNode<E> head = this;
    Stack<TreeNode<E>> stack = new Stack();
    while (!stack.isEmpty() || head != null) {
        if (head != null) {
            // 先将左结点全部入栈
            stack.push(head);
            head = head.left;
        } else {
            // 左结点全部入栈后就需要依次弹出，并处理右结点
            head = stack.pop();
            System.out.printf("%s ", head.value);
            head = head.right;
        }
    }
}

1.3 后序遍历

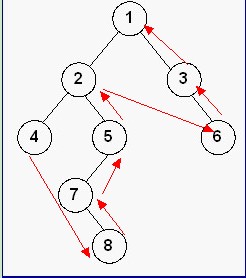
// 递归实现后序遍历
public void postOrder() {
    if (left != null) {
        left.preOrder1();
    }
    if (right != null) {
        right.preOrder1();
    }
    System.out.printf("%s ", value);
}

// 非递归实现后序遍历
public void postOrder2() {
    TreeNode<E> head = this;
    Stack<TreeNode<E>> stack1 = new Stack();
    Stack<TreeNode<E>> stack2 = new Stack();
    stack1.push(head);
    while (!stack1.isEmpty()) {
        TreeNode<E> tmp = stack1.pop();
        stack2.push(tmp);
        if (tmp.left != null) {
            stack1.push(tmp.left);
        }
        if (tmp.right != null) {
            stack1.push(tmp.right);
        }
    }
    while (!stack2.isEmpty()) {
        TreeNode<E> tmp = stack2.pop();
        System.out.printf("%s ", tmp.value);
    }
}

1.4 层次遍历

public void levelOrder() {
    TreeNode<E> head = this;
    Queue<TreeNode<E>> queue = new ArrayDeque<>();
    queue.offer(head);
    while (!queue.isEmpty()) {
        for (int i = 0; i < queue.size(); i++) {
            TreeNode<E> tmp = queue.poll();
            System.out.printf(String.valueOf(tmp.value) + " ");
            if (tmp.left != null) {
                queue.offer(tmp.left);
            }
            if (tmp.right != null) {
                queue.offer(tmp.right);
            }
        }
    }
}

二、树的深度

// 非递归求树的最大和最小深度
public int maxLevel() {
    int level = 0;
    TreeNode<E> head = this;
    Queue<TreeNode<E>> queue = new ArrayDeque<>();
    queue.offer(head);
    while (!queue.isEmpty()) {
        for (int i = 0; i < queue.size(); i++) {
            level++;
            TreeNode<E> tmp = queue.poll();
            if (tmp.left != null) {
                queue.offer(tmp.left);
            }
            if (tmp.right != null) {
                queue.offer(tmp.right);
            }
        }
    }
    return level;
}

public int minLevel() {
    int level = 0;
    TreeNode<E> head = this;
    Queue<TreeNode<E>> queue = new ArrayDeque<>();
    queue.offer(head);
    while (!queue.isEmpty()) {
        for (int i = 0; i < queue.size(); i++) {
            level++;
            TreeNode<E> tmp = queue.poll();
            if (tmp.left == null && tmp.right == null) {
                return level;
            }
            if (tmp.left != null) {
                queue.offer(tmp.left);
            }
            if (tmp.right != null) {
                queue.offer(tmp.right);
            }
        }
    }
    return 0;
}

// 递归求树的最大和最小深度
public int minLevel(TreeNode head) {
    if (head == null) {
        return 0;
    }
    if (head.left == null && head.right == null) {
        return 1;
    }
    if (head.left == null && head.right != null) {
        return minLevel(head.left) + 1;
    }
    if (head.left != null && head.right == null) {
        return minLevel(head.right) + 1;
    }
    return Math.min(minLevel(head.left), minLevel(head.right)) + 1;
}

三、求两个节点的公共祖先

// 递归求两个结点的公共祖先，一个结点可以是自己的祖先
public TreeNode ancestor(TreeNode root, TreeNode node1, TreeNode node2) {
    if (root == node1 || root == node2) {
        return root;
    }
    TreeNode left = ancestor(root.left, node1, node2);
    TreeNode right = ancestor(root.right, node1, node2);
    if (left == null || right == null) {
        return root;
    }
    return left != null ? left : right;
}

---

每天用心记录一点点。内容也许不重要，但习惯很重要！