布思算法——基于二进制队列的Java实现

Posted 2021-01-24 Edwin Xu

布思算法——基于二进制队列的Java实现

前面一篇提到二进制队列实现了 N位二进制的补码，那么我们来实现布思算法。

关于BinaryQueue：https://www.cnblogs.com/XT-xutao/p/10050518.html

 

先来思考：我们这样实现二进制乘法呢？

对于无符号整数，是可以转化为加法的：

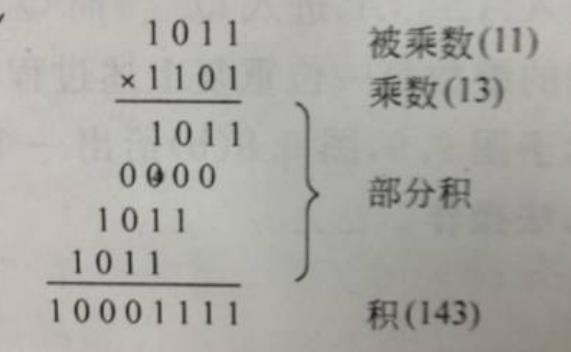
那么补码形式呢？好像一些也是可以用上面这种转化为加法的：

 

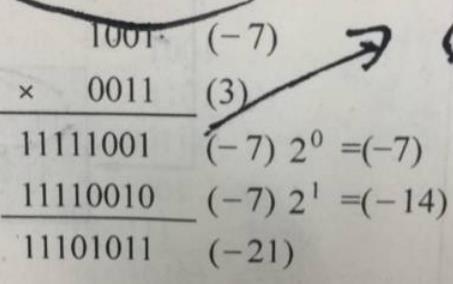
上面被乘数-7是小于0的，但是乘数为负的时候好像就不能工作了，因为不能正确地得出部分积。

怎么办呢？

还有一种方法： 就是在乘之前先判断符号，如果异号，则结果为负，用他们的绝对值形式乘就可以了，最后加符号就行。

但是，这种方法似乎太麻烦了，我们更偏向于——布思算法（BOOTH）

布思算法是基于： 2^n+2^n-1......2^n-k  =  2^(n+1) - 2^(n-k)

它有两大优点：

1.避免了如上的那种复杂操作。

2.减少了不必要的加法，节约了时间。

 

那么在计算机底层是怎么实现的呢？

可以用几个寄存器搞定：

A：附加寄存器，初始化0

Q：乘数寄存器

M：被乘数寄存器

Q0：乘数的最低位，初始化0

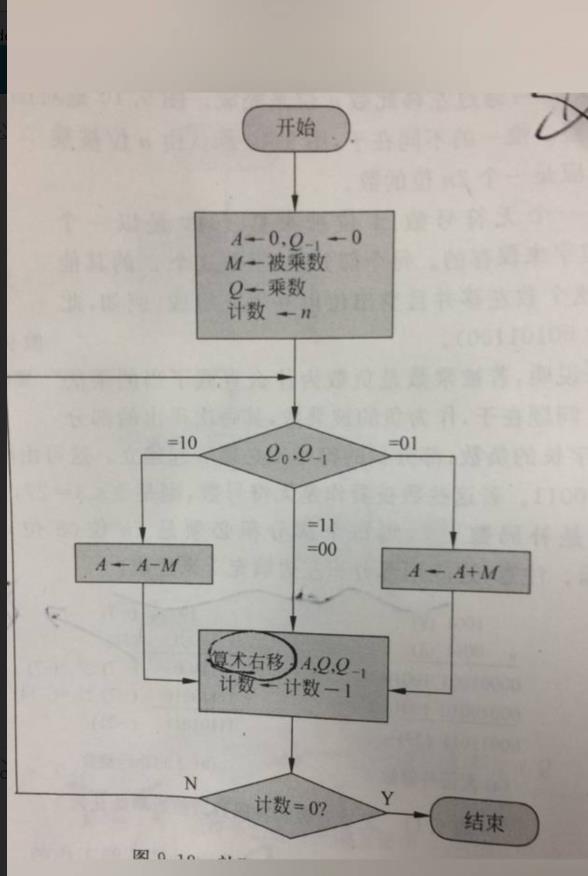
根据流程图就可以实现了。最后的结果是AQ寄存器里的值。

 

更新：前面讲那个BinaryQueue方法不好，直接用字符串形式的二进制表示更简单：

 1     public String multiply(String Q,String M){
 2         char Q0 = \'0\';
 3         String A = get01(Q.length(),"0");
 4         for (int i=0;i<Q.length();i++){
 5             String QQ0 =Q.charAt(Q.length()-1)+""+Q0;//不能把两个char字符放在一起，会变成加
 6             System.out.println(QQ0);
 7             if (QQ0.equals("10")){
 8                 A=substract(A,M).substring(1);
 9             }
10             else if (QQ0.equals("01")){
11                 A=add(A,M).substring(1);
12             }
13             String temp = shiftRight(A+Q+Q0);
14             A=temp.substring(0,A.length());
15             Q = temp.substring(A.length(),2*A.length());
16             Q0 = temp.charAt(temp.length()-1);
17         }
18         return A+Q;
19     }

 

那么代码怎么实现（BinaryQueue）呢？

 1 package com.computerOrganizationAndArchitecture.IntegerOperation;
 2 
 3 import com.computerOrganizationAndArchitecture.BinaryQueue;
 4 
 5 /**
 6  * Created by XuTao on 2018/12/1 19:27
 7  * 用BinaryQueue实现布思算法 （Java语言）
 8  */
 9 public class Booth {
10     BinaryQueue Q, M, A;  // Q：乘数； M：被乘数; A: 附加
11     private String n1,n2;
12     public Booth(String str1, String str2) {//要进行操作的两个二进制数的字符串模式
13         this.n1=str1;
14         this.n2=str2;
15         int len; // 最长的长度（如果两个二进制不一样长的话）
16         //扩展短的那个
17         if (n1.length() > n2.length()) {
18             String s = "";
19             len = n1.length() - n2.length();
20             for (int i = 0; i < len; i++) {
21                 s += n2.charAt(0);
22             }
23             n2 = s + n2;
24         }
25         else if (n1.length()<n2.length()){
26             String s = "";
27             len = n2.length() - n1.length();
28             for (int i = 0; i < len; i++) {
29                 s += n1.charAt(0);
30             }
31             n1 = s + n1;
32             System.out.println(n1);
33         }
34         else len = n1.length();
35 
36         Q = new BinaryQueue(n1);
37         M = new BinaryQueue(n2);
38         A = new BinaryQueue(len);
39         int Q0 = 0; //Q的最低位，初始化为0，用于判断要进行的操作
40 
41         System.out.println(A.getStr() + " " + Q.getStr() + " " + Q0 + " " + M.getStr());
42         for (int i = 0; i < len; i++) {
43             if (Q.getLast() == 1 && Q0 == 0) {//1-0 模式，A= A-M，
44                 A = A.subtract(M);
45             } else if (Q.getLast() == 0 && Q0 == 1) {
46                 A = A.add(M);
47             }
48             //AQQ0右移一位
49             Q0 = Q.getLast();
50             Q.shiftRight();
51             Q.set(0, A.getLast());
52             A.shiftRightArithmetically();
53 
54             System.out.println(A.getStr() + " " + Q.getStr() + " " + Q0 + " " + M.getStr());
55         }
56         BinaryQueue bq = new BinaryQueue(A.getStr() + Q.getStr());// A + Q 
57         System.out.println(A.getStr() + Q.getStr());
58         System.out.println(bq.getInt());
59     }
60 
61     public static void main(String[] args) {
62         new Booth("0011", "1111");  //3 * -1 = -3
63         new Booth("111111", "001111");  //-1 * 15 = -15
64         new Booth("011110", "001111");  //30 * 15 = 450
65     }
66 
67 }

demo：

A    Q  Q0  M

0000 0011 0 1111   第0周期
0000 1001 1 1111   第1周期
0000 0100 1 1111   第2周期
1111 1010 0 1111   第3周期
1111 1101 0 1111   第4周期

结果：

11111101

-3

000000 111111 0 001111
111000 111111 1 001111
111100 011111 1 001111
111110 001111 1 001111
111111 000111 1 001111
111111 100011 1 001111
111111 110001 1 001111
111111110001
-15

000000 011110 0 001111
000000 001111 0 001111
111000 100111 1 001111
111100 010011 1 001111
111110 001001 1 001111
111111 000100 1 001111
000111 000010 0 001111
000111000010
450