转载+补充“最简单的” 相机透视投影矩阵推导与解析
Posted ShaderJoy
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了转载+补充“最简单的” 相机透视投影矩阵推导与解析相关的知识,希望对你有一定的参考价值。
原文链接
作者:大其心宏其量扩其识
链接:https://www.jianshu.com/p/09fef48e7b0f
来源:简书
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
原文写得很好,但是主题格式我不太喜欢,所以我对文章的格式和重点的部分进行了 补充校正,方便自己日后阅读
正文
相机透视投影矩阵的 目标 是将 视锥体 内的顶点映射到 规范观察立方体 (NDC)内
以前总是记不住透视投影矩阵的推导,现在回过头翻看其实就可以总结为以下 4 步
- 相似三角形
- 人为构造
- 线性映射
- 解方程
- 透视锥到标准设备坐标
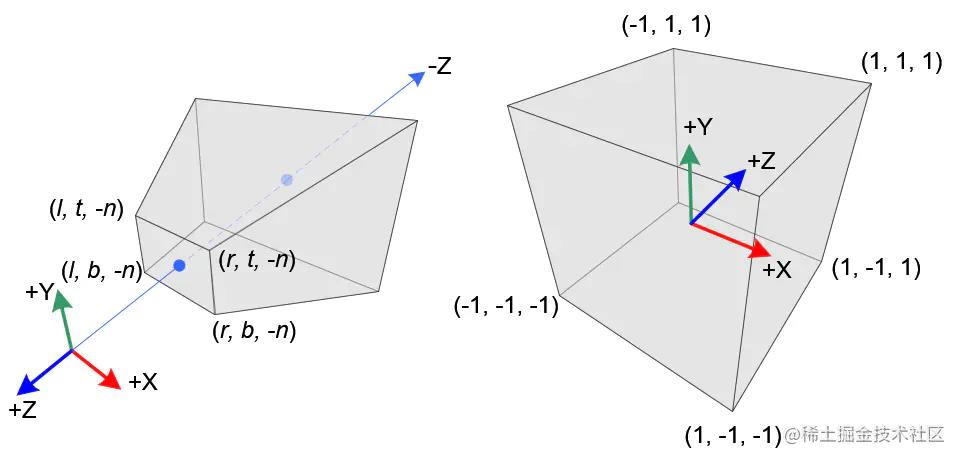
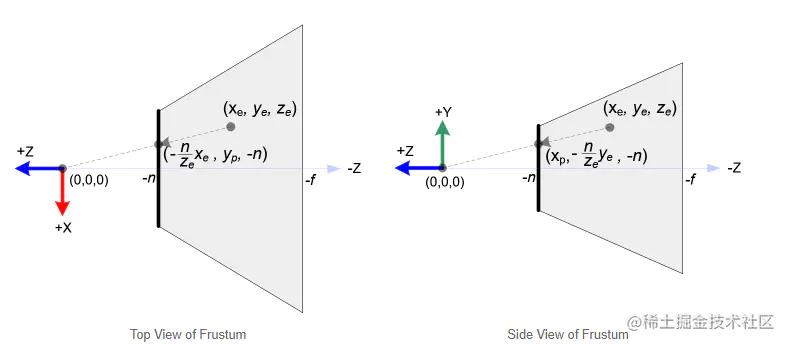
相似三角形计算( x e x_e xe-> x p x_p xp 和 y e y_e ye-> y p y_p yp)
先用 相似三角形 的原理,计算出 x e x_e xe 和 y e y_e ye 在 近裁剪面 上的投影 $x_p 和 $ y p y_p yp
- 左:顶视图 右:侧视图
先计算 x 轴

同理,再计算 y 轴

人为构造第四行
因为
x
p
x_p
xp,
y
p
y_p
yp 都与
−
z
e
-z_e
−ze 成反比,因为相机空间的坐标被 GL_PROJECTION 矩阵转换后还是 齐次坐标,最终得到 NDC 坐标是通过除以 裁剪坐标 的
w
w
w 元素来得到的,所以把
−
z
e
-z_e
−ze 当作裁剪坐标的
w
w
w 元素

线性映射(得到第一、二行)
接下来根据
x
p
x_p
xp->
x
n
x_n
xn,
y
p
y_p
yp->
y
n
y_n
yn 的 线性映射 关系:[r,l]->[1, -1], [b,t]->[1, -1] 得出归一后公式(一次函数)

把 x p x_p xp 与 y p y_p yp 代入到公式中

方程里的每一项都除以 − z e -z_e −ze, 那么 括号里的 就变成了 裁剪坐标 x c x_c xc, y c y_c yc
这样,已经推导出了 第一行 与 第二行

解方程(得到第三行的 A 与 B)
求
z
n
z_n
zn 与
x
n
x_n
xn,
y
n
y_n
yn 不太一样,所有点的
z
e
z_e
ze 投影到 近裁剪面 上以后都是相同的,但是我们要用
z
e
z_e
ze 来进行裁剪与深度测试, 所以我们要 反向投影。Z 轴与 X,Y 轴是无关联的,可以用 Z 轴与 近裁剪面 与 远裁剪面 相交的两个特殊点 (0,0,-n,1), (0,0,-f,1), 反推出映射关系中的 A,B

因为在相机空间中, w e w_e we 是 1 所以简化为

在规则观察体里 -n 映射成 -1, -f 映射成 1,代入方程

解方程求出 A,B

得到最终矩阵
再把 z e z_e ze 与 z n z_n zn 的关系代入

- OpenGL Perspective Projection Matrix

如果相机视锥是对称的,r=-l, t=-b,投影矩阵可以简化为

可恶的非线性
需要 注意 到 z e z_e ze 与 z n z_n zn 的关系 不是线性 的,离 近裁剪面 近的时候变化很大,远的时候变化很小,这会导致深度的精度问题,所以尽可能使用 小一些 的深度值
- Comparison of depth precision
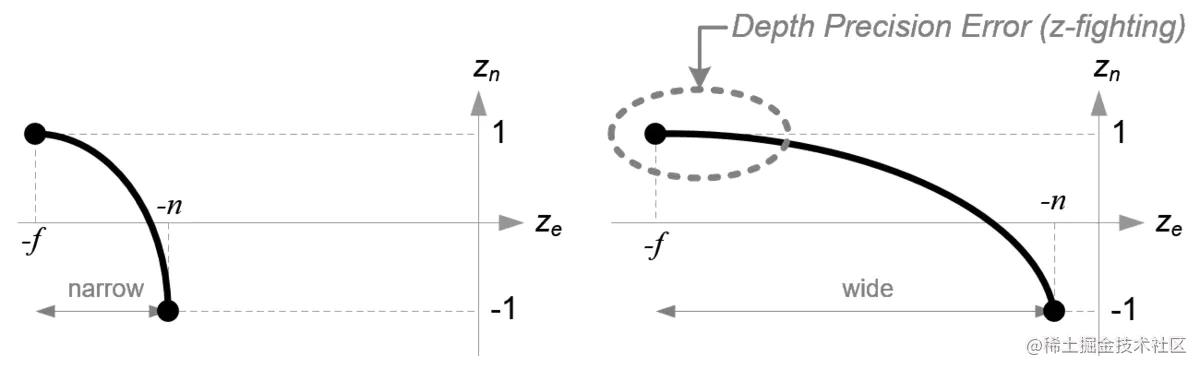
(kuso! )
也是因为这个 非线性 问题,导致 透视除法 被延后到了 顶点着色器和片元着色器之间,不然顶点着色器后的插值会出问题。
实际的裁剪
实际硬件上的裁剪步骤是在 裁剪空间 的齐次坐标(顶点着色器中经过 MVP 变换得到)下就完成的,而不是经过透视除法后(顶点着色器和片元着色器之间)的 NDC 空间中,即 xyz 分别和 w 进行比较[注0],而不是除了 w 后再和 [-1,1] 进行比较

注0:据说硬件上在 xy 上的裁剪还会乘上一个 guardband 系数 扩大范围
参考
以上是关于转载+补充“最简单的” 相机透视投影矩阵推导与解析的主要内容,如果未能解决你的问题,请参考以下文章