sklearn cookbook 总结
Posted zzulp
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了sklearn cookbook 总结相关的知识,希望对你有一定的参考价值。
Sklearn cookbook总结
1 数据预处理
1.1 获取数据
sklearn自带一些数据集,可以通过datasets模块的load_*方法加载,还有一些数据集比较大,可以通过fetch_*的方式下载。下面的代码示例了加载boston的房价数据和下载california的房价数据的方法。
from sklearn import datasets
boston = datasets.load_boston()
print(boston.DESCR)
california = datasets.fetch_california_housing('./temp')
# print(california.DESCR)
Boston House Prices dataset
===========================
Notes
------
Data Set Characteristics:
:Number of Instances: 506
:Number of Attributes: 13 numeric/categorical predictive
:Median Value (attribute 14) is usually the target
:Attribute Information (in order):
- CRIM per capita crime rate by town
- ZN proportion of residential land zoned for lots over 25,000 sq.ft.
- INDUS proportion of non-retail business acres per town
- CHAS Charles River dummy variable (= 1 if tract bounds river; 0 otherwise)
- NOX nitric oxides concentration (parts per 10 million)
- RM average number of rooms per dwelling
- AGE proportion of owner-occupied units built prior to 1940
- DIS weighted distances to five Boston employment centres
- RAD index of accessibility to radial highways
- TAX full-value property-tax rate per $10,000
- PTRATIO pupil-teacher ratio by town
- B 1000(Bk - 0.63)^2 where Bk is the proportion of blacks by town
- LSTAT % lower status of the population
- MEDV Median value of owner-occupied homes in $1000's
:Missing Attribute Values: None
:Creator: Harrison, D. and Rubinfeld, D.L.
This is a copy of UCI ML housing dataset.
http://archive.ics.uci.edu/ml/datasets/Housing
This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University.
The Boston house-price data of Harrison, D. and Rubinfeld, D.L. 'Hedonic
prices and the demand for clean air', J. Environ. Economics & Management,
vol.5, 81-102, 1978. Used in Belsley, Kuh & Welsch, 'Regression diagnostics
...', Wiley, 1980. N.B. Various transformations are used in the table on
pages 244-261 of the latter.
The Boston house-price data has been used in many machine learning papers that address regression
problems.
**References**
- Belsley, Kuh & Welsch, 'Regression diagnostics: Identifying Influential Data and Sources of Collinearity', Wiley, 1980. 244-261.
- Quinlan,R. (1993). Combining Instance-Based and Model-Based Learning. In Proceedings on the Tenth International Conference of Machine Learning, 236-243, University of Massachusetts, Amherst. Morgan Kaufmann.
- many more! (see http://archive.ics.uci.edu/ml/datasets/Housing)
1.2 数据处理
sklearn的preprocess模块提供了若干预处理数据的方法。其功能如下:
| 类或方法 | 作用 |
|---|---|
| StandardScaler | 数据减去均值后除以方差 |
| MinMaxScaler | 减去最小值除以最大最小值的差 |
| normalize | 将数据除以所有点的平方和 |
| binary | 由设置的阀值s进行二值化,x>s?1:0 |
其使用示例如下,由于是二维数组,计算在列上进行,即axis为0:
import numpy as np
from sklearn import preprocessing
a = np.array([[4., 2.], [2., 4.], [2, -2]], dtype=np.float)
print(a)
scaler = preprocessing.StandardScaler()
r = scaler.fit_transform(a)
print(r)
scaler = preprocessing.MinMaxScaler()
r = scaler.fit_transform(a)
print(r)
r = preprocessing.normalize(a)
print(r)
binary = preprocessing.Binarizer(3.5)
r = binary.fit_transform(a)
print(r)
[[ 4. 2.]
[ 2. 4.]
[ 2. -2.]]
[[ 1.41421356 0.26726124]
[-0.70710678 1.06904497]
[-0.70710678 -1.33630621]]
[[1. 0.66666667]
[0. 1. ]
[0. 0. ]]
[[ 0.89442719 0.4472136 ]
[ 0.4472136 0.89442719]
[ 0.70710678 -0.70710678]]
[[1. 0.]
[0. 1.]
[0. 0.]]
###1.3 分类编码
对于类别型的数据,需要将其数值化,以支持向量运算。
对于数值型的,可以使用preprocessing包的OneHotEncoder;对于字符串型的需要借助feature_extraction模块来进行。
from sklearn import preprocessing
from sklearn.feature_extraction import DictVectorizer
labels = [[1], [2], [3], [2]]
onehot = preprocessing.OneHotEncoder()
y = onehot.fit_transform(labels)
print(y.toarray())
labels = ['kind':'apple', 'kind':'orange']
dv = DictVectorizer()
y = dv.fit_transform(labels)
print(y.toarray())
labels = [1,2,3,3,2,1]
lb = preprocessing.LabelBinarizer()
vec = lb.fit_transform(labels)
print(vec)
[[1. 0. 0.]
[0. 1. 0.]
[0. 0. 1.]
[0. 1. 0.]]
[[1. 0.]
[0. 1.]]
[[1 0 0]
[0 1 0]
[0 0 1]
[0 0 1]
[0 1 0]
[1 0 0]]
1.4 缺失值处理
缺失值可以表示为nan,但在计算中无法使用,因此根据需要可以填充为合适的值。sklearn和pandas都能处理缺失值。
import pandas as pd
from sklearn import preprocessing
data = np.array([[1, 2], [np.nan, 4]])
print('origin:\\n', data)
imputer = preprocessing.Imputer(strategy='mean')
r = imputer.fit_transform(data)
print('sklean:\\n', r)
data_df = pd.DataFrame(data)
df = data_df.fillna(data_df.mean())
print('pandas\\n',df)
origin:
[[ 1. 2.]
[nan 4.]]
sklean:
[[1. 2.]
[1. 4.]]
pandas
0 1
0 1.0 2.0
1 1.0 4.0
1.5 去除无用的维度
PCA是sklearn的一个分解模块,可以借助它来完成数据降维。
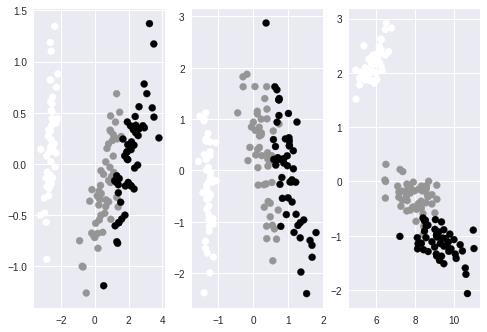
下面的代码对iris的特征进行PCA降维,通过对各维度的贡献分析,96%的变量可以由前两个主成分表示。因此可以把数据降低到前两维上,通过对PCA的参数n_components指定维度或比例,可以将数据进行降维。在只有两维的数据上通过plot作图以验证数据的可分性。
降维的另一个方法是使用FactorAnalysis类,使用上和PCA类似。其支持的核函数有liner, poly, rbf, sigmoid, cosine。
最后,利用矩阵的SVD也可以实现数据降维。各种降维方法的示例代码及效果如下:
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.decomposition import PCA, FactorAnalysis
from sklearn.decomposition import TruncatedSVD
iris = datasets.load_iris()
pca = PCA()
dt = pca.fit_transform(iris.data)
print(pca.explained_variance_ratio_)
'''
array([ 8.05814643e-01, 1.63050854e-01, 2.13486883e-02,......)
'''
fig, axes = plt.subplots(1,3)
pca = decomposition.PCA(n_components = 2)
dt = pca.fit_transform(iris.data)
axes[0].scatter(dt[:,0], dt[:,1], c=iris.target)
fa = FactorAnalysis(n_components=2)
dt = fa.fit_transform(iris.data)
axes[1].scatter(dt[:,0], dt[:,1], c=iris.target)
svd = TruncatedSVD()
dt = svd.fit_transform(iris.data)
axes[2].scatter(dt[:,0], dt[:,1], c=iris.target)
[0.92461621 0.05301557 0.01718514 0.00518309]
<matplotlib.collections.PathCollection at 0x7f2d406d9ef0>
1.6 使用pipeline连接多个变换
对于多步处理,pipeline提供了一种便捷的组织代码的方式。如下示例:
from sklearn import pipeline, preprocessing, decomposition, datasets
iris = datasets.load_iris()
imputer = preprocessing.Imputer()
pca = decomposition.PCA(n_components=2)
line = [('imputer', imputer), ('pca', pca)]
pipe = pipeline.Pipeline(line)
dt = pipe.fit_transform(iris.data)
print dt.shape #(150,2)
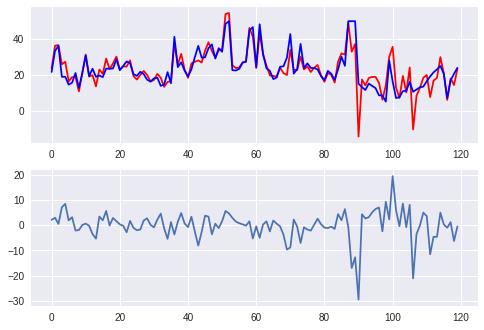
1.7 利用高斯随机过程处理回归
如果假设变量的分布和自变量符合高斯分布或正态分布,则可以使用高斯过程来进行回归分析。
from sklearn import datasets
from sklearn.gaussian_process import GaussianProcess
boston = datasets.load_boston()
sel = np.random.choice([True, False], len(boston.data), p=[0.75, 0.25])
gp = GaussianProcess()
gp.fit(boston.data[sel], boston.target[sel])
pred = gp.predict(boston.data[~sel])
diff = pred - boston.target[~sel]
xtick = range(len(pred))
fig, axes = plt.subplots(2,1)
axes[0].plot(xtick, pred, c='red',label='predict')
axes[0].plot(xtick, boston.target[~sel], c='blue', label='real')
axes[1].plot(xtick, diff)
plt.show()
/usr/local/lib/python3.6/dist-packages/sklearn/utils/deprecation.py:58: DeprecationWarning: Class GaussianProcess is deprecated; GaussianProcess was deprecated in version 0.18 and will be removed in 0.20. Use the GaussianProcessRegressor instead.
warnings.warn(msg, category=DeprecationWarning)
/usr/local/lib/python3.6/dist-packages/sklearn/utils/deprecation.py:77: DeprecationWarning: Function l1_cross_distances is deprecated; l1_cross_distances was deprecated in version 0.18 and will be removed in 0.20.
warnings.warn(msg, category=DeprecationWarning)
/usr/local/lib/python3.6/dist-packages/sklearn/utils/deprecation.py:77: DeprecationWarning: Function constant is deprecated; The function constant of regression_models is deprecated in version 0.19.1 and will be removed in 0.22.
warnings.warn(msg, category=DeprecationWarning)
/usr/local/lib/python3.6/dist-packages/sklearn/utils/deprecation.py:77: DeprecationWarning: Function squared_exponential is deprecated; The function squared_exponential of correlation_models is deprecated in version 0.19.1 and will be removed in 0.22.
warnings.warn(msg, category=DeprecationWarning)
/usr/local/lib/python3.6/dist-packages/sklearn/utils/deprecation.py:77: DeprecationWarning: Function constant is deprecated; The function constant of regression_models is deprecated in version 0.19.1 and will be removed in 0.22.
warnings.warn(msg, category=DeprecationWarning)
/usr/local/lib/python3.6/dist-packages/sklearn/utils/deprecation.py:77: DeprecationWarning: Function squared_exponential is deprecated; The function squared_exponential of correlation_models is deprecated in version 0.19.1 and will be removed in 0.22.
warnings.warn(msg, category=DeprecationWarning)
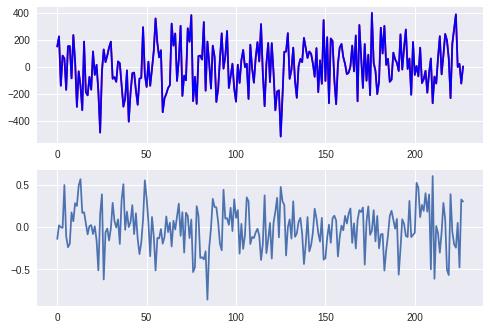
1.8 SGD处理回归
from sklearn import datasets
from sklearn.linear_model import SGDRegressor
X, y = datasets.make_regression(1000)
sel = np.random.choice([True, False], len(X), p=[0.75, 0.25])
sgd = SGDRegressor(max_iter=10, tol=0.1)
sgd.fit(X[sel], y[sel])
pred = sgd.predict(X[~sel])
diff = pred - y[~sel]
xtick = range(len(pred))
fig, axes = plt.subplots(2,1)
axes[0].plot(xtick, pred, c='red',label='predict')
axes[0].plot(xtick, y[~sel], c='blue', label='real')
axes[1].plot(xtick, diff)
plt.show()
2 线性模型
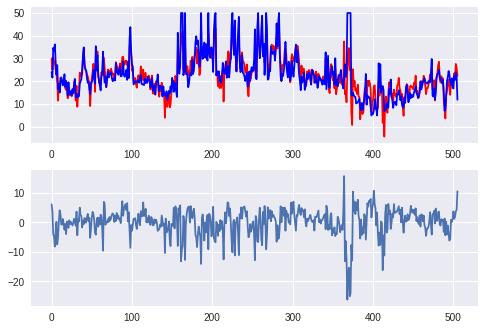
2.1 线性回归模型
from sklearn import datasets
from sklearn import linear_model
boston = datasets.load_boston()
model = linear_model.LinearRegression()
model.fit(boston.data, boston.target)
print(model.coef_)
pred = model.predict(boston.data)
diff = pred - boston.target
xtick = range(len(pred))
fig, axes = plt.subplots(2,1)
axes[0].plot(xtick, pred, c='red',label='predict')
axes[0].plot(xtick, boston.target, c='blue', label='real')
axes[1].plot(xtick, diff)
plt.show()
[-1.07170557e-01 4.63952195e-02 2.08602395e-02 2.68856140e+00
-1.77957587e+01 3.80475246e+00 7.51061703e-04 -1.47575880e+00
3.05655038e-01 -1.23293463e-02 -9.53463555e-01 9.39251272e-03
-5.25466633e-01]
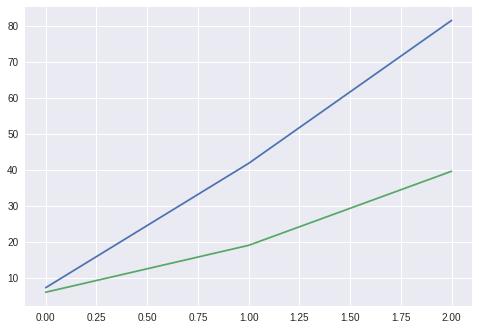
2.2 岭回归
岭回归在处理非满秩的矩阵时比较有用。 它可以去除不相关的系数。
为了找到合适的参数,可以使用交叉验证的方法。
from sklearn.datasets import make_regression
from sklearn.linear_model import LinearRegression, Ridge, RidgeCV
X, y = make_regression(n_samples=100, n_features=3, effective_rank=2, noise=5)
lr = LinearRegression()
lr.fit(X, y)
ridge = Ridge()
ridge.fit(X,y)
_, ax = plt.subplots(1,1)
ax.plot(range(len(lr.coef_)), lr.coef_)
ax.plot(range(len(ridge.coef_)), ridge.coef_)
plt.show()
ridge_cv = RidgeCV(alphas=[0.05, 0.08 ,0.1, 0.2, 0.8])
ridge_cv.fit(X, y)
print(ridge_cv.alpha_)
0.05
2.3 LASSO正则化
通过加入惩罚系数,消除系数之间的相关性。
如下示例所示,使用线性回归得到系数全部是相关的,但使用lasso处理后,只有5个是相关的。
为了找到lasso正则化合适的参数,我们需要使用交叉验证来寻找最优的参数。
from sklearn.linear_model import Lasso, LinearRegression
from sklearn.datasets import make_regression
X, y = make_regression(n_samples=1000, n_features=500, n_informative=5, noise=10)
lr = LinearRegression()
lr.fit(X, y)
print(np.sum(lr.coef_ !=0))
lasso = Lasso()
lasso.fit(X, y)
print(np.sum(lasso.coef_ !=0))
from sklearn.linear_model import LassoCV
lasso_cv = LassoCV()
lasso_cv.fit(X, y)
print(lasso_cv.alpha_)
500
6
0.7173410510859349
2.6 LARS正则化
LARS是一种回归手段,用于解决高维问题,即特征数远大于样本数量。LARS好处是可以设定一个较小的特征数量,防止数据的过拟合。LarsCV也可用来探索最优的参数。
from sklearn.datasets import make_regression
from sklearn.linear_model import Lars
X, y = make_regression(n_samples=200, n_features=500, n_informative=10, noise=2)
lars = Lars(n_nonzero_coefs=10)
lars.fit(X, y)
print(np.sum(lars.coef_ != 0 ))
10
2.7 逻辑回归
逻辑回归和上面的线性回归使用方法类似。
from sklearn.linear_model import LogisticRegression
from sklearn import datasets
iris = datasets.load_iris()
lr = LogisticRegression()
lr.fit(iris.data[:100], iris.target[:100])
pred = lr.predict(iris.data[100:])
diff = pred - iris.target[100:]
print(diff)
[-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1
-1 -1]
2.8 Bayes岭回归
from sklearn import datasets
from sklearn.linear_model import BayesianRidge
import matplotlib.pyplot as plt
boston = datasets.load_boston()
beyes = BayesianRidge()
beyes.fit(boston.data, boston.target)
print(beyes.coef_)
bayes = BayesianRidge(alpha_1=10, lambda_1=10)
beyes.fit(boston.data, boston.target)
print(beyes.coef_)
[-0.10035603 0.04970825 -0.04362901 1.89550379 -2.14222918 3.66953449
-0.01058388 -1.24482568 0.27964471 -0.01405975 -0.79764042 0.01011661
-0.56264033]
[-0.10035603 0.04970825 -0.04362901 1.89550379 -2.14222918 3.66953449
-0.01058388 -1.24482568 0.27964471 -0.01405975 -0.79764042 0.01011661
-0.56264033]
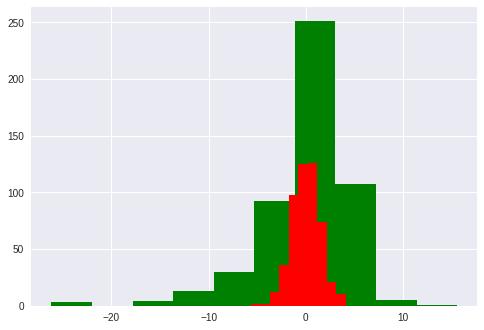
2.9 GBR回归
梯度提升树(GradientBoosting)是一种集成学习方法。在ensemble模块中提供了BGR供使用,下面的代码示例了GBR的使用方法,并与Linear模型的误差进行对比。
from sklearn import datasets
from sklearn.ensemble import GradientBoostingRegressor as GBR
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
boston = datasets.load_boston()
lr = LinearRegression()
lr.fit(boston.data, boston.target)
pred = lr.predict(boston.data)
diff = pred - boston.target
plt.hist(diff, color='g')
gbr = GBR(n_estimators=100, max_depth=3, loss='ls')
gbr.fit(boston.data, boston.target)
pred = gbr.predict(boston.data)
diff = pred - boston.target
plt.hist(diff, color='r')
(array([ 2., 2., 12., 36., 98., 125., 126., 74., 21., 10.]),
array([-5.64276266, -4.66928597, -3.69580928, -2.72233259, -1.7488559 ,
-0.77537921, 0.19809748, 1.17157417, 2.14505086, 3.11852755,
4.09200424]),
<a list of 10 Patch objects>)
3 聚类模型
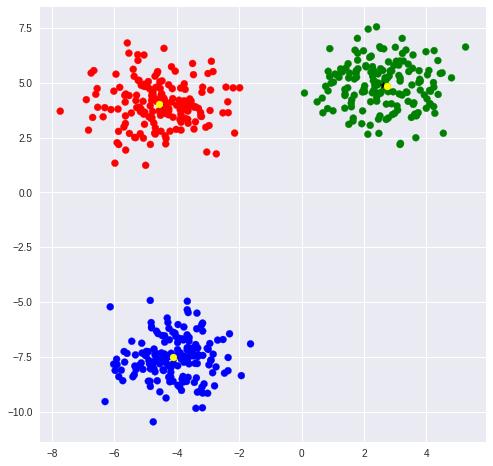
3.1 使用KMeans进行聚类
KMeans是最为常用的聚类方式,在cluster模块中可以找到KMeans类。通过指定中心数量可以令模型进行无监督聚类。
KMeans实例对象属性labels_保存了所有点的聚类标签,可以通过标签观察同一类的点。
当数据量很大时,KMeans计算很慢,这时可以使用Mini Batch KMeans来加速计算。
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
import numpy as np
from sklearn.cluster import KMeans, MiniBatchKMeans
rgb=np.array(['r', 'g', 'b'])
blobs, classes = make_blobs(500, centers=3)
_, ax = plt.subplots(figsize=(8,8))
ax.scatter(blobs[:,0], blobs[:, 1], color=rgb[classes])
kmean = KMeans(n_clusters=3)
kmean.fit(blobs)
print(kmean.cluster_centers_)
#for kind in range(len(classes)):
# print(blobs[kmean.labels_== kind])
ax.scatter(kmean.cluster_centers_[:,0], kmean.cluster_centers_[:,1], marker='*', color='black')
mb_kmean = MiniBatchKMeans(n_clusters=3, batch_size=100)
mb_kmean.fit(blobs, classes)
print(mb_kmean.cluster_centers_)
ax.scatter(mb_kmean.cluster_centers_[:,0], mb_kmean.cluster_centers_[:,1], marker='o', color='yellow')
[[ 2.62505603 4.87281732]
[-4.10154624 -7.5409836 ]
[-4.5489481 4.00556156]]
[[ 2.72677398 4.8618203 ]
[-4.10933407 -7.50669163]
[-4.56130824 4.04383432]]
<matplotlib.collections.PathCollection at 0x7fdc49868ba8>
3.2 优化聚类的数量
使用Silhouette距离的均值来衡量聚类结果的好坏,在metrics模块中可以找到silhouette_score方法来计算得分。
通过计算一系列的不同的聚类数量的得分,通常得分最高的位置附近是比较好的聚类数量取值。
from sklearn import metrics
from sklearn.datasets import make_blobs
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
blobs, classes = make_blobs(500, centers=3)
scores = []
for k in range(2, 30):
kmean = KMeans(n_clusters=k)
kmean.fit(blobs, classes)
scores.append(metrics.silhouette_score