Java中双基准快速排序方法(DualPivotQuicksort.sort())的具体实现
Posted chang4
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了Java中双基准快速排序方法(DualPivotQuicksort.sort())的具体实现相关的知识,希望对你有一定的参考价值。
在Java语言的Arrays类下提供了一系列排序(sort)方法,帮助使用者对各种不同数据类型的数组进行排序. 在1.7之后的版本中, Arrays.sort()方法在操作过程中实际调用的是DualPivotQuicksort类下的sort方法,DualPivotQuicksort和Arrays一样,都在java.util包下,按字面翻译过来,就是双(Dual)基准(Pivot)快速排序(Quicksort)算法.
双基准快速排序算法于2009年由Vladimir Yaroslavskiy提出,是对经典快速排序(Classic Quicksort)进行优化后的一个版本, Java自1.7开始,均使用此方法作为默认排序算法. 接下来,本文就将对此方法的具体实现过程进行简单的介绍.
在正式进入对DualPivotQuicksort的介绍之前,我们先来对经典快速排序的实现思路进行一下简单的了解:
经典快速排序在操作过程中首先会从数组中选取一个基准(Pivot),这个基准可以是数组中的任意一个元素;
随后,将这个数组所有其他元素和Pivot进行比较,比Pivot小的数放在左侧,大的数放在右侧;
如此,我们就在Pivot的左侧和右侧各得到了一个新的数组;
接下来我们再在这两个新的数组中各自选取新的Pivot,把小的放在左侧,大的放在右侧,循环往复,最终就会得到由小到大顺序排列的数组.
下图(via wiki)便是Quicksort的一个具体实现:
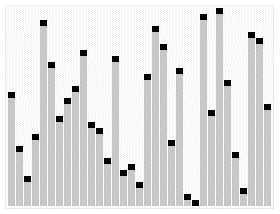
在对Quicksort的基本思路有了一定了解之后,下一步我们就来看Java中DualPivotQuicksort.sort是如何实现的;
本方法在实际工作过程中, 并不是对任何传入的数组都直接进行快速排序, 而是会先对数组进行一系列测试, 然后根据数组的具体情况选择最适合的算法来进行排序,下面我们结合源码来看:
首先, 以一个int数组为例,
当一个数组int[] a被传入DualPivotQuicksort.sort()时,该方法还会要求其他一系列参数:
1 static void sort(int[] a, int left, int right, int[] work, int workBase, int workLen)
其中,int[] a是需被排序的int数组, left和right是该数组中需要被排序的部分的左右界限. 而后面的work, workBase和workLen三个参数其实并不会参与双基准快速排序, 而是当系统认为本数组更适合使用归并排序(merge sort)的时候, 供归并排序使用.
但是,在实际使用中,我们并不希望为了排序设置这么多的参数,因此:
Arrays.sort()在调用DualPivotQuicksort.sort()之前,对int数组的排序提供了两种参数列表:
public static void sort(int[] a)
直接对int[] a 进行排序,以及:
public static void sort(int[] a, int fromIndex, int toIndex)
对int[] a 中从fromIndex到toIndex(包头不包尾)之间的元素进行排序.
在这里,Arrays.sort()会自动将int[] work, int workBase, int workLen设置为null,0,0 省去了使用者的麻烦.
紧接着,DualPivotQuicksort.sort()会对传入的int数组进行检测, 具体流程如下: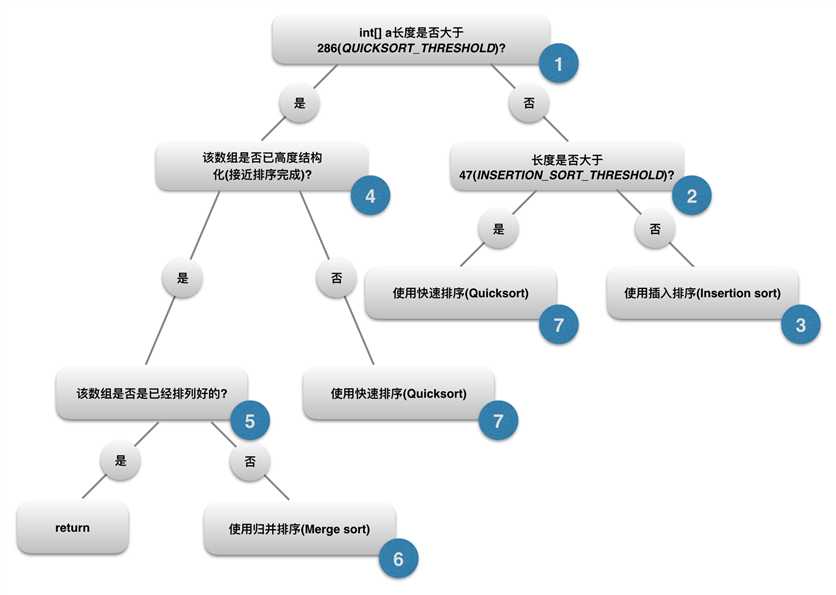
这里先贴上整个方法的完整源码, 然后按上图中的流程逐步分析, 只想看DualPivotQuicksort的话可以直接跳到下面第7点:

1 /** 2 * Sorts the specified range of the array using the given 3 * workspace array slice if possible for merging 4 * 5 * @param a the array to be sorted 6 * @param left the index of the first element, inclusive, to be sorted 7 * @param right the index of the last element, inclusive, to be sorted 8 * @param work a workspace array (slice) 9 * @param workBase origin of usable space in work array 10 * @param workLen usable size of work array 11 */ 12 static void sort(int[] a, int left, int right, 13 int[] work, int workBase, int workLen) { 14 // Use Quicksort on small arrays 15 if (right - left < QUICKSORT_THRESHOLD) { 16 sort(a, left, right, true); 17 return; 18 } 19 20 /* 21 * Index run[i] is the start of i-th run 22 * (ascending or descending sequence). 23 */ 24 int[] run = new int[MAX_RUN_COUNT + 1]; 25 int count = 0; run[0] = left; 26 27 // Check if the array is nearly sorted 28 for (int k = left; k < right; run[count] = k) { 29 if (a[k] < a[k + 1]) { // ascending 30 while (++k <= right && a[k - 1] <= a[k]); 31 } else if (a[k] > a[k + 1]) { // descending 32 while (++k <= right && a[k - 1] >= a[k]); 33 for (int lo = run[count] - 1, hi = k; ++lo < --hi; ) { 34 int t = a[lo]; a[lo] = a[hi]; a[hi] = t; 35 } 36 } else { // equal 37 for (int m = MAX_RUN_LENGTH; ++k <= right && a[k - 1] == a[k]; ) { 38 if (--m == 0) { 39 sort(a, left, right, true); 40 return; 41 } 42 } 43 } 44 45 /* 46 * The array is not highly structured, 47 * use Quicksort instead of merge sort. 48 */ 49 if (++count == MAX_RUN_COUNT) { 50 sort(a, left, right, true); 51 return; 52 } 53 } 54 55 // Check special cases 56 // Implementation note: variable "right" is increased by 1. 57 if (run[count] == right++) { // The last run contains one element 58 run[++count] = right; 59 } else if (count == 1) { // The array is already sorted 60 return; 61 } 62 63 // Determine alternation base for merge 64 byte odd = 0; 65 for (int n = 1; (n <<= 1) < count; odd ^= 1); 66 67 // Use or create temporary array b for merging 68 int[] b; // temp array; alternates with a 69 int ao, bo; // array offsets from ‘left‘ 70 int blen = right - left; // space needed for b 71 if (work == null || workLen < blen || workBase + blen > work.length) { 72 work = new int[blen]; 73 workBase = 0; 74 } 75 if (odd == 0) { 76 System.arraycopy(a, left, work, workBase, blen); 77 b = a; 78 bo = 0; 79 a = work; 80 ao = workBase - left; 81 } else { 82 b = work; 83 ao = 0; 84 bo = workBase - left; 85 } 86 87 // Merging 88 for (int last; count > 1; count = last) { 89 for (int k = (last = 0) + 2; k <= count; k += 2) { 90 int hi = run[k], mi = run[k - 1]; 91 for (int i = run[k - 2], p = i, q = mi; i < hi; ++i) { 92 if (q >= hi || p < mi && a[p + ao] <= a[q + ao]) { 93 b[i + bo] = a[p++ + ao]; 94 } else { 95 b[i + bo] = a[q++ + ao]; 96 } 97 } 98 run[++last] = hi; 99 } 100 if ((count & 1) != 0) { 101 for (int i = right, lo = run[count - 1]; --i >= lo; 102 b[i + bo] = a[i + ao] 103 ); 104 run[++last] = right; 105 } 106 int[] t = a; a = b; b = t; 107 int o = ao; ao = bo; bo = o; 108 } 109 } 110 111 /** 112 * Sorts the specified range of the array by Dual-Pivot Quicksort. 113 * 114 * @param a the array to be sorted 115 * @param left the index of the first element, inclusive, to be sorted 116 * @param right the index of the last element, inclusive, to be sorted 117 * @param leftmost indicates if this part is the leftmost in the range 118 */ 119 private static void sort(int[] a, int left, int right, boolean leftmost) { 120 int length = right - left + 1; 121 122 // Use insertion sort on tiny arrays 123 if (length < INSERTION_SORT_THRESHOLD) { 124 if (leftmost) { 125 /* 126 * Traditional (without sentinel) insertion sort, 127 * optimized for server VM, is used in case of 128 * the leftmost part. 129 */ 130 for (int i = left, j = i; i < right; j = ++i) { 131 int ai = a[i + 1]; 132 while (ai < a[j]) { 133 a[j + 1] = a[j]; 134 if (j-- == left) { 135 break; 136 } 137 } 138 a[j + 1] = ai; 139 } 140 } else { 141 /* 142 * Skip the longest ascending sequence. 143 */ 144 do { 145 if (left >= right) { 146 return; 147 } 148 } while (a[++left] >= a[left - 1]); 149 150 /* 151 * Every element from adjoining part plays the role 152 * of sentinel, therefore this allows us to avoid the 153 * left range check on each iteration. Moreover, we use 154 * the more optimized algorithm, so called pair insertion 155 * sort, which is faster (in the context of Quicksort) 156 * than traditional implementation of insertion sort. 157 */ 158 for (int k = left; ++left <= right; k = ++left) { 159 int a1 = a[k], a2 = a[left]; 160 161 if (a1 < a2) { 162 a2 = a1; a1 = a[left]; 163 } 164 while (a1 < a[--k]) { 165 a[k + 2] = a[k]; 166 } 167 a[++k + 1] = a1; 168 169 while (a2 < a[--k]) { 170 a[k + 1] = a[k]; 171 } 172 a[k + 1] = a2; 173 } 174 int last = a[right]; 175 176 while (last < a[--right]) { 177 a[right + 1] = a[right]; 178 } 179 a[right + 1] = last; 180 } 181 return; 182 } 183 184 // Inexpensive approximation of length / 7 185 int seventh = (length >> 3) + (length >> 6) + 1; 186 187 /* 188 * Sort five evenly spaced elements around (and including) the 189 * center element in the range. These elements will be used for 190 * pivot selection as described below. The choice for spacing 191 * these elements was empirically determined to work well on 192 * a wide variety of inputs. 193 */ 194 int e3 = (left + right) >>> 1; // The midpoint 195 int e2 = e3 - seventh; 196 int e1 = e2 - seventh; 197 int e4 = e3 + seventh; 198 int e5 = e4 + seventh; 199 200 // Sort these elements using insertion sort 201 if (a[e2] < a[e1]) { int t = a[e2]; a[e2] = a[e1]; a[e1] = t; } 202 203 if (a[e3] < a[e2]) { int t = a[e3]; a[e3] = a[e2]; a[e2] = t; 204 if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; } 205 } 206 if (a[e4] < a[e3]) { int t = a[e4]; a[e4] = a[e3]; a[e3] = t; 207 if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t; 208 if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; } 209 } 210 } 211 if (a[e5] < a[e4]) { int t = a[e5]; a[e5] = a[e4]; a[e4] = t; 212 if (t < a[e3]) { a[e4] = a[e3]; a[e3] = t; 213 if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t; 214 if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; } 215 } 216 } 217 } 218 219 // Pointers 220 int less = left; // The index of the first element of center part 221 int great = right; // The index before the first element of right part 222 223 if (a[e1] != a[e2] && a[e2] != a[e3] && a[e3] != a[e4] && a[e4] != a[e5]) { 224 /* 225 * Use the second and fourth of the five sorted elements as pivots. 226 * These values are inexpensive approximations of the first and 227 * second terciles of the array. Note that pivot1 <= pivot2. 228 */ 229 int pivot1 = a[e2]; 230 int pivot2 = a[e4]; 231 232 /* 233 * The first and the last elements to be sorted are moved to the 234 * locations formerly occupied by the pivots. When partitioning 235 * is complete, the pivots are swapped back into their final 236 * positions, and excluded from subsequent sorting. 237 */ 238 a[e2] = a[left]; 239 a[e4] = a[right]; 240 241 /* 242 * Skip elements, which are less or greater than pivot values. 243 */ 244 while (a[++less] < pivot1); 245 while (a[--great] > pivot2); 246 247 /* 248 * Partitioning: 249 * 250 * left part center part right part 251 * +--------------------------------------------------------------+ 252 * | < pivot1 | pivot1 <= && <= pivot2 | ? | > pivot2 | 253 * +--------------------------------------------------------------+ 254 * ^ ^ ^ 255 * | | | 256 * less k great 257 * 258 * Invariants: 259 * 260 * all in (left, less) < pivot1 261 * pivot1 <= all in [less, k) <= pivot2 262 * all in (great, right) > pivot2 263 * 264 * Pointer k is the first index of ?-part. 265 */ 266 outer: 267 for (int k = less - 1; ++k <= great; ) { 268 int ak = a[k]; 269 if (ak < pivot1) { // Move a[k] to left part 270 a[k] = a[less]; 271 /* 272 * Here and below we use "a[i] = b; i++;" instead 273 * of "a[i++] = b;" due to performance issue. 274 */ 275 a[less] = ak; 276 ++less; 277 } else if (ak > pivot2) { // Move a[k] to right part 278 while (a[great] > pivot2) { 279 if (great-- == k) { 280 break outer; 281 } 282 } 283 if (a[great] < pivot1) { // a[great] <= pivot2 284 a[k] = a[less]; 285 a[less] = a[great]; 286 ++less; 287 } else { // pivot1 <= a[great] <= pivot2 288 a[k] = a[great]; 289 } 290 /* 291 * Here and below we use "a[i] = b; i--;" instead 292 * of "a[i--] = b;" due to performance issue. 293 */ 294 a[great] = ak; 295 --great; 296 } 297 } 298 299 // Swap pivots into their final positions 300 a[left] = a[less - 1]; a[less - 1] = pivot1; 301 a[right] = a[great + 1]; a[great + 1] = pivot2; 302 303 // Sort left and right parts recursively, excluding known pivots 304 sort(a, left, less - 2, leftmost); 305 sort(a, great + 2, right, false); 306 307 /* 308 * If center part is too large (comprises > 4/7 of the array), 309 * swap internal pivot values to ends. 310 */ 311 if (less < e1 && e5 < great) { 312 /* 313 * Skip elements, which are equal to pivot values. 314 */ 315 while (a[less] == pivot1) { 316 ++less; 317 } 318 319 while (a[great] == pivot2) { 320 --great; 321 } 322 323 /* 324 * Partitioning: 325 * 326 * left part center part right part 327 * +----------------------------------------------------------+ 328 * | == pivot1 | pivot1 < && < pivot2 | ? | == pivot2 | 329 * +----------------------------------------------------------+ 330 * ^ ^ ^ 331 * | | | 332 * less k great 333 * 334 * Invariants: 335 * 336 * all in (*, less) == pivot1 337 * pivot1 < all in [less, k) < pivot2 338 * all in (great, *) == pivot2 339 * 340 * Pointer k is the first index of ?-part. 341 */ 342 outer: 343 for (int k = less - 1; ++k <= great; ) { 344 int ak = a[k]; 345 if (ak == pivot1) { // Move a[k] to left part 346 a[k] = a[less]; 347 a[less] = ak; 348 ++less; 349 } else if (ak == pivot2) { // Move a[k] to right part 350 while (a[great] == pivot2) { 351 if (great-- == k) { 352 break outer; 353 } 354 } 355 if (a[great] == pivot1) { // a[great] < pivot2 356 a[k] = a[less]; 357 /* 358 * Even though a[great] equals to pivot1, the 359 * assignment a[less] = pivot1 may be incorrect, 360 * if a[great] and pivot1 are floating-point zeros 361 * of different signs. Therefore in float and 362 * double sorting methods we have to use more 363 * accurate assignment a[less] = a[great]. 364 */ 365 a[less] = pivot1; 366 ++less; 367 } else { // pivot1 < a[great] < pivot2 368 a[k] = a[great]; 369 } 370 a[great] = ak; 371 --great; 372 } 373 } 374 } 375 376 // Sort center part recursively 377 sort(a, less, great, false); 378 379 } else { // Partitioning with one pivot 380 /* 381 * Use the third of the five sorted elements as pivot. 382 * This value is inexpensive approximation of the median. 383 */ 384 int pivot = a[e3]; 385 386 /* 387 * Partitioning degenerates to the traditional 3-way 388 * (or "Dutch National Flag") schema: 389 * 390 * left part center part right part 391 * +-------------------------------------------------+ 392 * | < pivot | == pivot | ? | > pivot | 393 * +-------------------------------------------------+ 394 * ^ ^ ^ 395 * | | | 396 * less k great 397 * 398 * Invariants: 399 * 400 * all in (left, less) < pivot 401 * all in [less, k) == pivot 402 * all in (great, right) > pivot 403 * 404 * Pointer k is the first index of ?-part. 405 */ 406 for (int k = less; k <= great; ++k) { 407 if (a[k] == pivot) { 408 continue; 409 } 410 int ak = a[k]; 411 if (ak < pivot) { // Move a[k] to left part 412 a[k] = a[less]; 413 a[less] = ak; 414 ++less; 415 } else { // a[k] > pivot - Move a[k] to right part 416 while (a[great] > pivot) { 417 --great; 418 } 419 if (a[great] < pivot) { // a[great] <= pivot 420 a[k] = a[less]; 421 a[less] = a[great]; 422 ++less; 423 } else { // a[great] == pivot 424 /* 425 * Even though a[great] equals to pivot, the 426 * assignment a[k] = pivot may be incorrect, 427 * if a[great] and pivot are floating-point 428 * zeros of different signs. Therefore in float 429 * and double sorting methods we have to use 430 * more accurate assignment a[k] = a[great]. 431 */ 432 a[k] = pivot; 433 } 434 a[great] = ak; 435 --great; 436 } 437 } 438 439 /* 440 * Sort left and right parts recursively. 441 * All elements from center part are equal 442 * and, therefore, already sorted. 443 */ 444 sort(a, left, less - 1, leftmost); 445 sort(a, great + 1, right, false); 446 } 447 }
1. 判断数组int[] a的长度是否大于常量QUICKSORT_THRESHOLD, 即286:
286是java设定的一个阈值,当数组长度小于此值时, 系统将不再考虑merge sort, 直接将参数传入本类中的另一个私有sort方法进行排序,
private static void sort(long[] a, int left, int right, boolean leftmost)

1 // Use Quicksort on small arrays 2 if (right - left < QUICKSORT_THRESHOLD) { 3 sort(a, left, right, true); 4 return; 5 }
2. 继续判断int[] a的长度是否大于常量INSERTION_SORT_THRESHOLD, 即47:
3. 若数组长度小于47, 则使用insertion sort:
数组传入本类私有的sort方法后, 会继续判断数组长度是否大于47, 若小于此值, 则直接使用insertion sort并返回结果, 因为插入算法并非本文重点, 此处不再展开叙述,

1 int length = right - left + 1; 2 3 // Use insertion sort on tiny arrays 4 if (length < INSERTION_SORT_THRESHOLD) { 5 if (leftmost) { 6 /* 7 * Traditional (without sentinel) insertion sort, 8 * optimized for server VM, is used in case of 9 * the leftmost part. 10 */ 11 for (int i = left, j = i; i < right; j = ++i) { 12 int ai = a[i + 1]; 13 while (ai < a[j]) { 14 a[j + 1] = a[j]; 15 if (j-- == left) { 16 break; 17 } 18 } 19 a[j + 1] = ai; 20 } 21 } else { 22 /* 23 * Skip the longest ascending sequence. 24 */ 25 do { 26 if (left >= right) { 27 return; 28 } 29 } while (a[++left] >= a[left - 1]); 30 31 /* 32 * Every element from adjoining part plays the role 33 * of sentinel, therefore this allows us to avoid the 34 * left range check on each iteration. Moreover, we use 35 * the more optimized algorithm, so called pair insertion 36 * sort, which is faster (in the context of Quicksort) 37 * than traditional implementation of insertion sort. 38 */ 39 for (int k = left; ++left <= right; k = ++left) { 40 int a1 = a[k], a2 = a[left]; 41 42 if (a1 < a2) { 43 a2 = a1; a1 = a[left]; 44 } 45 while (a1 < a[--k]) { 46 a[k + 2] = a[k]; 47 } 48 a[++k + 1] = a1; 49 50 while (a2 < a[--k]) { 51 a[k + 1] = a[k]; 52 } 53 a[k + 1] = a2; 54 } 55 int last = a[right]; 56 57 while (last < a[--right]) { 58 a[right + 1] = a[right]; 59 } 60 a[right + 1] = last; 61 } 62 return; 63 }
值得注意的是, java在这里提供了两种不同的插入排序算法, 当传入的参数leftmost真假值不同时, 会使用不同的算法.
leftmost代表的是本次传入的数组是否是从最初的int[] a的最左侧left开始的, 因为本方法在整个排序过程中可能会针对数组的不同部分被多次调用, 因此leftmost有可能为false.
Quicksort的情况我们放到最后再谈, 这里先回过来看第一步判断中数组长度大于286的情形, 这种情况下, 系统会
4.继续判断该数组是否已经高度结构化(即已经接近排序完成):
这里的基本思路是这样的:
a. 定义一个常量MAX_RUN_COUNT = 67;
b. 定义一个计数器int count = 0; 定义一个数组int[] run 使之长度为MAX_RUN_COUNT + 1;
c. 令run[0] = left, 然后从传入数组的最左侧left开始遍历, 若数组的前n个元素均为升序/降序排列, 而第n + 1个元素的升/降序发生了改变, 则将第n个元素的索引存入run[1], 同时++count, 此时count的值为1;
d. 从n + 1开始继续遍历, 直至升/降序再次改变, 再将此处的索引存入run[2], ++count, 此时count的值为2, 以此类推...
......
e. 若将整个数组全部遍历完成后, count仍然小于MAX_RUN_COUNT (即整个数组升降序改变的次数低于67次), 证明该数组是高度结构化的, 则使用merge sort进行排序;
若count == MAX_RUN_COUNT时, 还未完成对数组的遍历, 则证明数组并非高度结构化, 则调用前文所述私有sort方法进行quicksort.

1 /* 2 * Index run[i] is the start of i-th run 3 * (ascending or descending sequence). 4 */ 5 int[] run = new int[MAX_RUN_COUNT + 1]; 6 int count = 0; run[0] = left; 7 8 // Check if the array is nearly sorted 9 for (int k = left; k < right; run[count] = k) { 10 if (a[k] < a[k + 1]) { // ascending 11 while (++k <= right && a[k - 1] <= a[k]); 12 } else if (a[k] > a[k + 1]) { // descending 13 while (++k <= right && a[k - 1] >= a[k]); 14 for (int lo = run[count] - 1, hi = k; ++lo < --hi; ) { 15 int t = a[lo]; a[lo] = a[hi]; a[hi] = t; 16 } 17 } else { // equal 18 for (int m = MAX_RUN_LENGTH; ++k <= right && a[k - 1] == a[k]; ) { 19 if (--m == 0) { 20 sort(a, left, right, true); 21 return; 22 } 23 } 24 } 25 26 /* 27 * The array is not highly structured, 28 * use Quicksort instead of merge sort. 29 */ 30 if (++count == MAX_RUN_COUNT) { 31 sort(a, left, right, true); 32 return; 33 } 34 }
5. 判断该数组是否是是已经排列好的:
若该数组是高度结构化的, 在使用merge sort进行排序之前, 会先检验数组是否本身就是排序好的, 思路很简单, 如果在前面的检测中一次就完成了遍历, 就证明该数组是排序好的, 则直接返回结果:

1 // Check special cases 2 // Implementation note: variable "right" is increased by 1. 3 if (run[count] == right++) { // The last run contains one element 4 run[++count] = right; 5 } else if (count == 1) { // The array is already sorted 6 return; 7 }
*当然, 在具体实现中还有不少其他要考虑的因素, 有兴趣了解的话可以结合上一部分代码进行阅读.
6. 进行归并排序(merge sort):
此处不再展开叙述, 值得注意的是, 由于归并算法在操作过程中需要使用一块额外的存储空间, 本方法参数列表中要求的work, workBase和workLen三个参数就是在此处使用的:

1 // Determine alternation base for merge 2 byte odd = 0; 3 for (int n = 1; (n <<= 1) < count; odd ^= 1); 4 5 // Use or create temporary array b for merging 6 int[] b; // temp array; alternates with a 7 int ao, bo; // array offsets from ‘left‘ 8 int blen = right - left; // space needed for b 9 if (work == null || workLen < blen || workBase + blen > work.length) { 10 work = new int[blen]; 11 workBase = 0; 12 } 13 if (odd == 0) { 14 System.arraycopy(a, left, work, workBase, blen); 15 b = a; 16 bo = 0; 17 a = work; 18 ao = workBase - left; 19 } else { 20 b = work; 21 ao = 0; 22 bo = workBase - left; 23 } 24 25 // Merging 26 for (int last; count > 1; count = last) { 27 for (int k = (last = 0) + 2; k <= count; k += 2) { 28 int hi = run[k], mi = run[k - 1]; 29 for (int i = run[k - 2], p = i, q = mi; i < hi; ++i) { 30 if (q >= hi || p < mi && a[p + ao] <= a[q + ao]) { 31 b[i + bo] = a[p++ + ao]; 32 } else { 33 b[i + bo] = a[q++ + ao]; 34 } 35 } 36 run[++last] = hi; 37 } 38 if ((count & 1) != 0) { 39 for (int i = right, lo = run[count - 1]; --i >= lo; 40 b[i + bo] = a[i + ao] 41 ); 42 run[++last] = right; 43 } 44 int[] t = a; a = b; b = t; 45 int o = ao; ao = bo; bo = o; 46 }
7. 进行双基准快速排序(dual pivot quicksort):
只有在上述情况都不满足的情况下, 本方法才会使用双基准快速排序算法进行排序,
算法本身的思路并不复杂, 和经典快速排序相差不大, 顾名思义, 比起经典快排, 该算法选取了两个Pivot, 我们姑且称之为P1和P2.
P1和P2都从数组中选出, P1在P2的右侧, 且P1必须小于P2, 如果不是, 则交换P1和P2的值;
接下来令数组中的每一个元素和基准进行比较, 比P1小的放在P1左边, 比P2大的放在P2右边, 介于两者之间的放在中间.
这样, 最终我们会的得到三个数组, 比P1小元素构成的数组, 介于P1和P2之间的元素构成的数组, 以及比P2大的元素构成的数组.
最后, 递归地对这三个数组进行排序, 最终得到排序完成的结果.
思路上虽然, 并不复杂, 但Java为了尽可能的提高效率, 在对这个算法进行实现的过程中增加了非常多的细节, 下面我们就来大致看一下其中的部分内容:

1 // Inexpensive approximation of length / 7 2 int seventh = (length >> 3) + (length >> 6) + 1; 3 4 /* 5 * Sort five evenly spaced elements around (and including) the 6 * center element in the range. These elements will be used for 7 * pivot selection as described below. The choice for spacing 8 * these elements was empirically determined to work well on 9 * a wide variety of inputs. 10 */ 11 int e3 = (left + right) >>> 1; // The midpoint 12 int e2 = e3 - seventh; 13 int e1 = e2 - seventh; 14 int e4 = e3 + seventh; 15 int e5 = e4 + seventh; 16 17 // Sort these elements using insertion sort 18 if (a[e2] < a[e1]) { int t = a[e2]; a[e2] = a[e1]; a[e1] = t; } 19 20 if (a[e3] < a[e2]) { int t = a[e3]; a[e3] = a[e2]; a[e2] = t; 21 if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; } 22 } 23 if (a[e4] < a[e3]) { int t = a[e4]; a[e4] = a[e3]; a[e3] = t; 24 if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t; 25 if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; } 26 } 27 } 28 if (a[e5] < a[e4]) { int t = a[e5]; a[e5] = a[e4]; a[e4] = t; 29 if (t < a[e3]) { a[e4] = a[e3]; a[e3] = t; 30 if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t; 31 if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; } 32 } 33 } 34 } 35 36 // Pointers 37 int less = left; // The index of the first element of center part 38 int great = right; // The index before the first element of right part 39 40 if (a[e1] != a[e2] && a[e2] != a[e3] && a[e3] != a[e4] && a[e4] != a[e5]) { 41 /* 42 * Use the second and fourth of the five sorted elements as pivots. 43 * These values are inexpensive approximations of the first and 44 * second terciles of the array. Note that pivot1 <= pivot2. 45 */ 46 int pivot1 = a[e2]; 47 int pivot2 = a[e4]; 48 49 /* 50 * The first and the last elements to be sorted are moved to the 51 * locations formerly occupied by the pivots. When partitioning 52 * is complete, the pivots are swapped back into their final 53 * positions, and excluded from subsequent sorting. 54 */ 55 a[e2] = a[left]; 56 a[e4] = a[right]; 57 58 /* 59 * Skip elements, which are less or greater than pivot values. 60 */ 61 while (a[++less] < pivot1); 62 while (a[--great] > pivot2); 63 64 /* 65 * Partitioning: 66 * 67 * left part center part right part 68 * +--------------------------------------------------------------+ 69 * | < pivot1 | pivot1 <= && <= pivot2 | ? | > pivot2 | 70 * +--------------------------------------------------------------+ 71 * ^ ^ ^ 72 * | | | 73 * less k great 74 * 75 * Invariants: 76 * 77 * all in (left, less) < pivot1 78 * pivot1 <= all in [less, k) <= pivot2 79 * all in (great, right) > pivot2 80 * 81 * Pointer k is the first index of ?-part. 82 */ 83 outer: 84 for (int k = less - 1; ++k <= great; ) { 85 int ak = a[k]; 86 if (ak < pivot1) { // Move a[k] to left part 87 a[k] = a[less]; 88 /* 89 * Here and below we use "a[i] = b; i++;" instead 90 * of "a[i++] = b;" due to performance issue. 91 */ 92 a[less] = ak; 93 ++less; 94 } else if (ak > pivot2) { // Move a[k] to right part 95 while (a[great] > pivot2) { 96 if (great-- == k) { 97 break outer; 98 } 99 } 100 if (a[great] < pivot1) { // a[great] <= pivot2 101 a[k] = a[less]; 102 a[less] = a[great]; 103 ++less; 104 } else { // pivot1 <= a[great] <= pivot2 105 a[k] = a[great]; 106 } 107 /* 108 * Here and below we use "a[i] = b; i--;" instead 109 * of "a[i--] = b;" due to performance issue. 110 */ 111 a[great] = ak; 112 --great; 113 } 114 } 115 116 // Swap pivots into their final positions 117 a[left] = a[less - 1]; a[less - 1] = pivot1; 118 a[right] = a[great + 1]; a[great + 1] = pivot2; 119 120 // Sort left and right parts recursively, excluding known pivots 121 sort(a, left, less - 2, leftmost); 122 sort(a, great + 2, right, false); 123 124 /* 125 * If center part is too large (comprises > 4/7 of the array), 126 * swap internal pivot values to ends. 127 */ 128 if (less < e1 && e5 < great) { 129 /* 130 * Skip elements, which are equal to pivot values. 131 */ 132 while (a[less] == pivot1) { 133 ++less; 134 } 135 136 while (a[great] == pivot2) { 137 --great; 138 } 139 140 /* 141 * Partitioning: 142 * 143 * left part center part right part 144 * +----------------------------------------------------------+ 145 * | == pivot1 | pivot1 < && < pivot2 | ? | == pivot2 | 146 * +----------------------------------------------------------+ 147 * ^ ^ ^ 148 * | | | 149 * less k great 150 * 151 * Invariants: 152 * 153 * all in (*, less) == pivot1 154 * pivot1 < all in [less, k) < pivot2 155 * all in (great, *) == pivot2 156 * 157 * Pointer k is the first index of ?-part. 158 */ 159 outer: 160 for (int k = less - 1; ++k <= great; ) { 161 int ak = a[k]; 162 if (ak == pivot1) { // Move a[k] to left part 163 a[k] = a[less]; 164 a[less] = ak; 165 ++less; 166 } else if (ak == pivot2) { // Move a[k] to right part 167 while (a[great] == pivot2) { 168 if (great-- == k) { 169 break outer; 170 } 171 } 172 if (a[great] == pivot1) { // a[great] < pivot2 173 a[k] = a[less]; 174 /* 175 * Even though a[great] equals to pivot1, the 176 * assignment a[less] = pivot1 may be incorrect, 177 * if a[great] and pivot1 are floating-point zeros 178 * of different signs. Therefore in float and 179 * double sorting methods we have to use more 180 * accurate assignment a[less] = a[great]. 181 */ 182 a[less] = pivot1; 183 ++less; 184 } else { // pivot1 < a[great] < pivot2 185 a[k] = a[great]; 186 } 187 a[great] = ak; 188 --great; 189 } 190 } 191 } 192 193 // Sort center part recursively 194 sort(a, less, great, false); 195 196 } else { // Partitioning with one pivot 197 /* 198 * Use the third of the five sorted elements as pivot. 199 * This value is inexpensive approximation of the median. 200 */ 201 int pivot = a[e3]; 202 203 /* 204 * Partitioning degenerates to the traditional 3-way 205 * (or "Dutch National Flag") schema: 206 * 207 * left part center part right part 208 * +-------------------------------------------------+ 209 * | < pivot | == pivot | ? | > pivot | 210 * +-------------------------------------------------+ 211 * ^ ^ ^ 212 * | | | 213 * less k great 214 * 215 * Invariants: 216 * 217 * all in (left, less) < pivot 218 * all in [less, k) == pivot 219 * all in (great, right) > pivot 220 * 221 * Pointer k is the first index of ?-part. 222 */ 223 for (int k = less; k <= great; ++k) { 224 if (a[k] == pivot) { 225 continue; 226 } 227 int ak = a[k]; 228 if (ak < pivot) { // Move a[k] to left part 229 a[k] = a[less]; 230 a[less] = ak; 231 ++less; 232 } else { // a[k] > pivot - Move a[k] to right part 233 while (a[great] > pivot) { 234 --great; 235 } 236 if (a[great] < pivot) { // a[great] <= pivot 237 a[k] = a[less]; 238 a[less] = a[great]; 239 ++less; 240 } else { // a[great] == pivot 241 /* 242 * Even though a[great] equals to pivot, the 243 * assignment a[k] = pivot may be incorrect, 244 * if a[great] and pivot are floating-point 245 * zeros of different signs. Therefore in float 246 * and double sorting methods we have to use 247 * more accurate assignment a[k] = a[great]. 248 */ 249 a[k] = pivot; 250 } 251 a[great] = ak; 252 --great; 253 } 254 } 255 256 /* 257 * Sort left and right parts recursively. 258 * All elements from center part are equal 259 * and, therefore, already sorted. 260 */ 261 sort(a, left, less - 1, leftmost); 262 sort(a, great + 1, right, false); 263 }
首先, 也是本方法中最具特色的部分, 就是对Pivot的选取:
在这里, 系统会先通过位运算获取数组长度的1/7的近似值(位运算无法精确表示1/7)
int seventh = (length >> 3) + (length >> 6) + 1;
然后获取本数组中间位置的索引e3:
int e3 = (left + right) >>> 1; // The midpoint
在中间位置的左右1/7, 2/7处各获取两个索引(e1, e2, e4, e5):

int e2 = e3 - seventh; int e1 = e2 - seventh; int e4 = e3 + seventh; int e5 = e4 + seventh;
将这五个索引对应的值用插入算法进行有小到大的排序后, 再放回五个索引的位置

1 // Sort these elements using insertion sort 2 if (a[e2] < a[e1]) { int t = a[e2]; a[e2] = a[e1]; a[e1] = t; } 3 4 if (a[e3] < a[e2]) { int t = a[e3]; a[e3] = a[e2]; a[e2] = t; 5 if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; } 6 } 7 if (a[e4] < a[e3]) { int t = a[e4]; a[e4] = a[e3]; a[e3] = t; 8 if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t; 9 if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; } 10 } 11 } 12 if (a[e5] < a[e4]) { int t = a[e5]; a[e5] = a[e4]; a[e4] = t; 13 if (t < a[e3]) { a[e4] = a[e3]; a[e3] = t; 14 if (t < a[e2]) { a[e3] = a[e2]; a[e2] = t; 15 if (t < a[e1]) { a[e2] = a[e1]; a[e1] = t; } 16 } 17 } 18 }
接下来进行判断, 若这五个索引对应的元素值各不相同, 则选取e2的值作为Pivot1, e4的值作为Pivot2(特别注意基准是值而不是元素), 然后进行双基准快排, Java声称这种选法比其他方式更加高效;
但如果这五个值中有相同的存在, 则本轮排序选取e3的值作为Pivot, 进行单基准快排, 同样, Java声称这种选取方式要比随机选取更加高效.
至于具体排序的部分, 其实并没有太多可以叙述的内容, 值得注意的是, 由于在递归的过程中会不断地调用私有的sort方法, 所以在递归中获得的子数组长度小47时, 会改为调用插入排序.
此外, 源码中还有一些可以借鉴的用来提高效率的小窍门, 比如在对元素进行交换位置之前先过滤掉头尾处已经在正确位置的元素等, 有兴趣的话可以再对源码进行仔细阅读.
至此, 关于DualPivotQuicksort.sort()的大致实现过程的介绍也就基本结束了, 最后我们不妨进行一个简单的测试, 看看它是否真的比经典快排更加高效:
首先, 我们先来测试一下经典Quicksort的性能, 对包含一亿个Random.nextInt()随机数的数组进行排序, 重复十次求平均排序运行时间,
具体代码如下, 其中经典快排的代码摘自wiki快速排序条目:

1 import java.util.Date; 2 import java.util.Random; 3 4 public class Test { 5 public static void main(String[] args) { 6 //定义time记录总耗时 7 int time = 0; 8 9 //测试十次 10 for (int i = 0; i < 10; i++) { 11 //生成一个包含一亿个Random.nextInt()随机数的数组 12 Random r = new Random(); 13 int[] arr = new int[100000000]; 14 for (int j : arr) { 15 arr[j] = r.nextInt(); 16 } 17 18 //使用经典快排对数组进行排序,并获取运行时间 19 long t1 = new Date().getTime(); 20 qSort(arr, 0, arr.length - 1); 21 long t2 = new Date().getTime(); 22 23 //输出运行时间 24 System.out.print((int)(t2 - t1) + " "); 25 //对每次运行时间求和 26 time += (int)(t2 - t1); 27 28 } 29 //输出十次排序平均运行时间 30 System.out.println(time / 10); 31 } 32 33 public static void qSort(int[] arr, int head, int tail) { 34 if (head >= tail || arr == null || arr.length <= 1) { 35 return; 36 } 37 int i = head, j = tail, pivot = arr[(head + tail) / 2]; 38 while (i <= j) { 39 while (arr[i] < pivot) { 40 ++i; 41 } 42 while (arr[j] > pivot) { 43 --j; 44 } 45 if (i < j) { 46 int t = arr[i]; 47 arr[i] = arr[j]; 48 arr[j] = t; 49 ++i; 50 --j; 51 } else if (i == j) { 52 ++i; 53 } 54 } 55 qSort(arr, head, j); 56 qSort(arr, i, tail); 57 } 58 }
经过测试, 我们得到结果, 十次排序的运行时间分别为2405 3017 3021 2972 2993 2967 2992 2954 3001 2984(ms),
平均时间则是2930ms
接下来, 再对DualPivotQuicksort.sort()使用同样的方法进行测试, 直接用Arrays.sort()进行排序,代码如下:

1 import java.util.Arrays; 2 import java.util.Date; 3 import java.util.Random; 4 5 public class Test2 { 6 public static void main(String[] args) { 7 //定义time记录总耗时 8 int time = 0; 9 10 //测试十次 11 for (int i = 0; i < 10; i++) { 12 //生成一个包含一亿个Random.nextInt()随机数的数组 13 Random r = new Random(); 14 int[] arr = new int[100000000]; 15 for (int j : arr) { 16 arr[j] = r.nextInt(); 17 } 18 19 //使用经典快排对数组进行排序,并获取运行时间 20 long t1 = new Date().getTime(); 21 Arrays.sort(arr); 22 long t2 = new Date().getTime(); 23 24 //输出运行时间 25 System.out.print((int)(t2 - t1) + " "); 26 //对每次运行时间求和 27 time += (int)(t2 - t1); 28 29 } 30 //输出十次排序平均运行时间 31 System.out.println(time / 10); 32 } 33 }
十次运行时间分别是115 16 31 21 28 118 62 78 78 63(ms).
平均时间则达到了惊人的61ms.
当然, 之所以会产生如此巨大的差距, 一方面是因为双基准快排本身性能更加优秀, 另一方也是因为Java对该方法进行了大量的优化, 而选取测试的经典快排则相当粗糙, 只是这种算法思想的体现, 并不是说两种算法本身性能上存在着这种程度的差距.
Reference:
Quicksort - wiki
https://en.wikipedia.org/wiki/Quicksort
快速排序 - wiki
https://zh.wikipedia.org/zh-cn/%E5%BF%AB%E9%80%9F%E6%8E%92%E5%BA%8F
java.util.Arrays
java.util.DualPivotQuicksort
以上是关于Java中双基准快速排序方法(DualPivotQuicksort.sort())的具体实现的主要内容,如果未能解决你的问题,请参考以下文章
