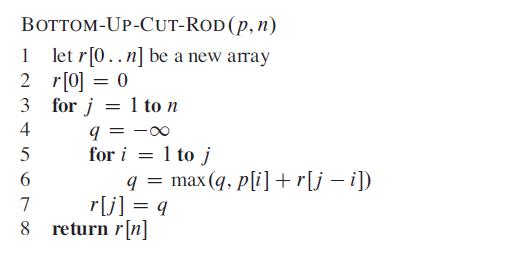Rod cutting - Using Dynamic Programming

Posted 2023-02-20 kasperskynod

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Rod cutting - Using Dynamic Programming相关的知识，希望对你有一定的参考价值。

1.Problem Description

Serling Enterprises buys long steel rods and cuts them into shorter rods, which it then sells. Each cut is free. The management of Serling Enterprises wants to know the best way to cut up the rods.
We assume that we know, for i = 1,2,…, the price $p_i$ in dollars that Serling Enterprises charges for a rod of length $i$ inches. Rod lengths are always an integral number of inches. Figure 1 gives a sample price table.

length

i $i$ 1 2 3 4 5 6 7 8 9 10 price

pi $p_i$ 1 5 8 9 10 17 17 20 24 30

Figrure 1:A sample price table for rods. Each rod of length $i$ inches earns the company $p_i$ dollars of revenue.

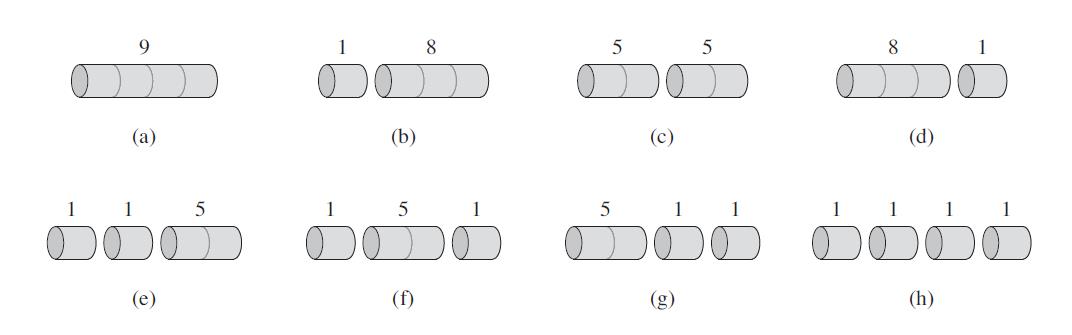
Figure 2:The 8 possible ways of cutting up a rod of length 4. Above each piece is the value of that piece, according to the sample price chart of Figure 1. The optimal strategy is part (c)—cutting the rod into two pieces of length 2—which has total value 10.

So can we find a strategy to cut a rod so that we can earn most?

2.Problem Analyse

We can easily find a exhaustive way to list all the possibilities and find a optimal one. For a rod of length 10 inches, there are $2^10$ possibilities in total. That’s really a big number! The algorithm grows in exponential way. So is there a algorithm which we can use to solve this problem using less time? Yes, dynamic programming is what we are looking for.

2.1 Optimal Substructure

Before we introduce dynamic programming, we should know what is optimal substructure.

If an optimal solution cuts the rod into k pieces, for some $1 \\leq k \\leq n$ , then an optimal decomposition

n=i1+i2+⋯+ik $n=i_1+i_2+\\dots+i_k$
of the rod into pieces of lengths

i1,i2,…,ik $i_1,i_2,\\dots,ik$ provides maximum corresponding revenue

rn=pi1+pi2+⋯+pik $r_n=p_i_1+p_i_2+\\dots+p_i_k$
More generally, we can frame the values

rn $r_n$ for

n≥1 $n\\ge 1$ in terms of optimal revenues from shorter rods:

rn=max(pn,r1+rn−1,r2+rn−2,…,rn−1+r1) $r_n=max(p_n,r_1+r_n-1,r_2+r_n-2,\\dots,r_n-1+r_1)$
The first argument,

pn $p_n$ ,corresponds to making no cuts at all and selling the rod of length

n $n$ as is. The other

n−1 $n-1$ arguments to max correspond to the maximum revenue obtained by making an initial cut of the rod into two pieces of size

i $i$ and

n−i $n-i$ , for each

i=1,2,…,n−1 $i=1,2,\\dots,n-1$ , and then optimally cutting up those pieces further, obtaining revenues

ri $r_i$ and

rn−i $r_n-i$ from those two pieces. Since we don’t know ahead of time which value of

i $i$ optimizes revenue, we have to consider all possible values for

i $i$ and pick the one that maximizes revenue. We also have the option of picking no

i $i$ at all if we can obtain more revenue by selling the rod uncut.

Note that to solve the original problem of size

n $n$ , we solve smaller problems of the same type, but of smaller sizes. Once we make the first cut, we may consider the two pieces as independent instances of the rod-cutting problem. The overall optimal solution incorporates optimal solutions to the two related subproblems, maximizing revenue from each of those two pieces. We say that the rod-cutting problem exhibits optimal substructure: optimal solutions to a problem incorporate optimal solutions to related subproblems, which we may solve independently.

2.2 Using dynamic programming for optimal rod cutting

We now show how to convert CUT-ROD into an efficient algorithm, using dynamic programming.

Dynamic programming thus uses additional memory to save computation time; it serves an example of a time-memory trade-off. The savings may be dramatic: an exponential-time solution may be transformed into a polynomial-time solution.There are usually two equivalent ways to implement a dynamic-programming approach: top-down with memoization and bottom-up method. We will only introduce bottom-up method since it is more efficient.

Bottom-up method typically depends on some natural notion of the “size” of a subproblem, such that solving any particular subproblem depends only on solving “smaller” subproblems. We sort the subproblems by size and solve them in size order, smallest first. When solving a particular subproblem, we have already solved all of the smaller subproblems its solution depends upon, and we have saved their solutions. We solve each subproblem only once, and when we first see it, we have already solved all of its prerequisite subproblems.

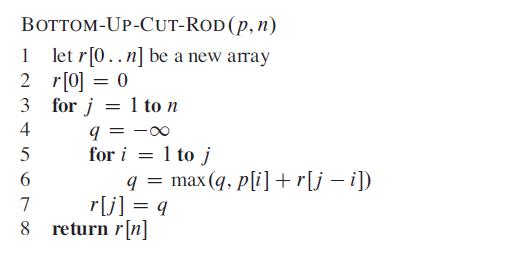
For the bottom-up dynamic-programming approach, BOTTOM-UP-CUT-ROD uses the natural ordering of the subproblems: a problem of size $i$ is “smaller” than a subproblem of size $j$ if $i < j$ . Thus, the procedure solves subproblems of sizes $j=0,1,\\dots,n$ , in that order.

3.Code

double rodCutting(unsigned n, vector<double> &p) 
    vector<double> cost(n, -1);
    double max = -1;
    for (auto i = 0; i < n; ++i) 
        for (auto j = 0; j <= i; ++j) 
            if (j == 0)
                max = p[i];
            else 
                if (cost[j - 1] + cost[i - j] > max)
                    max = cost[j - 1] + cost[i - j];
            
        
        cost[i] = max;
        max = -1;
       
    return cost[n - 1];

References

[1] Introduction to Algorithms(Third Edition), page 360 to 370.

以上是关于Rod cutting - Using Dynamic Programming的主要内容，如果未能解决你的问题，请参考以下文章