已知权函数=1+x^2,区间服[负1,1],求首项系数为1的正交多项式,n=0,1,2,3,4
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了已知权函数=1+x^2,区间服[负1,1],求首项系数为1的正交多项式,n=0,1,2,3,4相关的知识,希望对你有一定的参考价值。
不会解答,麻烦各位了
1、将闭区间[0, 1]等分成n份,在每一个小区间上直接计算梯形面zhi积(上下底为(x^3)/3.0),并合并求和。
2、将闭区间[0, 1]等分成shu(2 * n)份,重复上述操作。
3、上述两步的结果做差,如果绝对值小于,如: 1e-6,那么输出第二步的结果;否则继续加倍等分区间重复操作。
数学分析:
f(x)=x^2=x*x;
定积分:x*x*x/3+c(常数)
在区间(0,1)上定积分:1/3=0.333333
结果正确。
常用的正交多项式:
1、勒让德多项式
2、切比雪夫多项式
3、拉盖尔多项式
4、埃尔米特多项式
推广为如下形式:
设ψ(x)是区间【α,b】上的非减函数,。如果定义在【α,b】上的函数ƒ(x)与g(x)满足等式,则称他们在[α,b]上关于权 ψ(x)正交。这里的积分是勒贝格-斯蒂尔杰斯意义下的积分。
为区别上述情况,人们称这时的权函数 ψ(x)为积分权,而将前面的权函数ω(x)称作微分权。由积分权出发建立的正交多项式理论自然要广泛一些。此外,还可建立多元的正交多项式理论。
以上内容参考 百度百科-正交多项式
参考技术A1、将闭区间[0, 1]等分成n份,在每一个小区间上直接计算梯形面zhi积(上下底为(x^3)/3.0),并合并求和;
2、将闭区间[0, 1]等分成shu(2 * n)份,重复上述操作;
3、上述两步的结果做差,如果绝对值小于,如: 1e-6,那么输出第二步的结果;否则继续加倍等分区间重复操作。
数学分析:
f(x)=x^2=x*x;
定积分:x*x*x/3+c(常数)
在区间(0,1)上定积分:1/3=0.333333
结果正确。
扩展资料:
可以算出,此时递推公式(2)中的 α=β的情况比较简单,称作超球多项式。当α=β=0,也即关于权时,相应的正交多项式称作勒让德多项式,它还可表成 当,也即关于权相应的正交多项式称作切比雪夫多项式,它有表达式当,也即关于权,相应的正交多项式称作第二类切比雪夫多项式,它有表达式
这些正交多项式的正交区间都是[-1,1]。它们不仅本身有广泛的应用,而且其零点还常作为插值过程的结点。此外,还是二阶线性齐次微分方程 的解。
参考资料来源;百度百科-正交多项式
参考技术B
你好,我刚才才看到,请问一下,n=0.第一个为什么是1呀
追答不是要首项系数为1咯?
因为首系数1定义的p0是1,然后勒让德多项式下去
本回答被提问者采纳概率论与数理统计猴博士 笔记 p21-23 二维连续型求边缘分布函数和密度函数,已知两个边缘密度函数求f(x,y)
二维连续型求边缘分布函数
题型如下:给出F(x,y),让我们求F(x),F(y)

步骤:
F
X
(
x
)
=
F
(
x
,
+
∞
)
F
Y
(
y
)
=
F
(
+
∞
,
y
)
F_X(x)=F(x,+∞) \\\\F_Y(y)=F(+∞,y)
FX(x)=F(x,+∞)FY(y)=F(+∞,y)
直接做上面那道例题:

二维连续型求边缘密度函数
题干:给出F(x,y),让我们求f(x),f(y)

方法:
f
X
(
x
)
=
∫
−
∞
+
∞
f
(
x
,
y
)
d
y
f
Y
(
y
)
=
∫
−
∞
+
∞
f
(
x
,
y
)
d
x
f_X(x)=\\displaystyle \\int^+∞_-∞f(x,y)dy \\\\f_Y(y)=\\displaystyle \\int^+∞_-∞f(x,y)dx
fX(x)=∫−∞+∞f(x,y)dyfY(y)=∫−∞+∞f(x,y)dx
步骤:

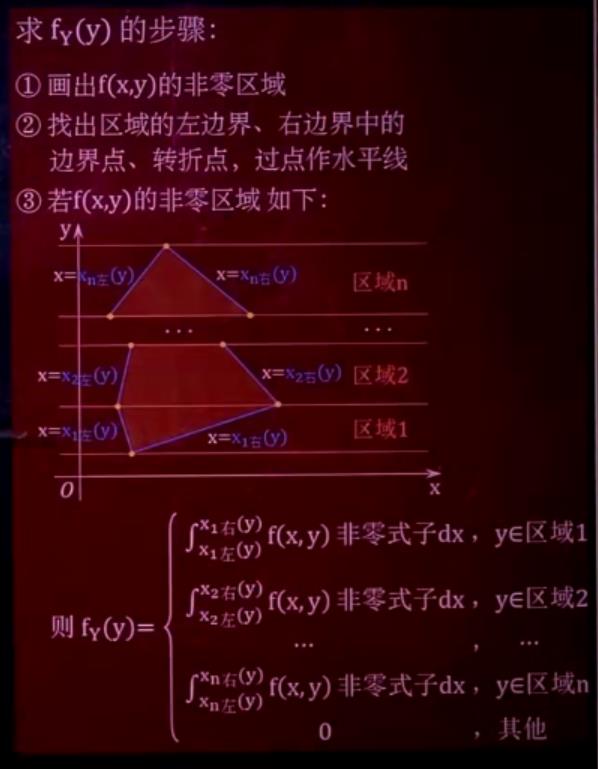
我们以例1为例做一下:
第一步:

第二步:
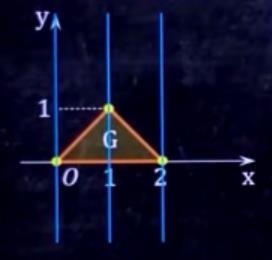
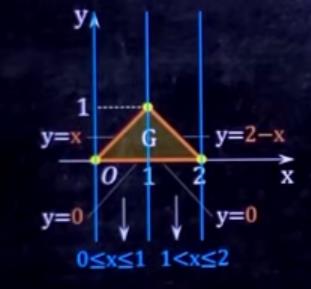
第三步:**因为是求f(x),所以要作垂直于x轴的线。**最左边的蓝线和最右边的蓝线中间有几个格,公式里就会有几个区域。
这道题有两个区域。每个区域的积分上限是上边界的表达式,下限是下边界的表达式。这里是求f(x),所以是对x的表达式。

然后得出答案:

求f(y)同理:
要作垂直于y轴的线
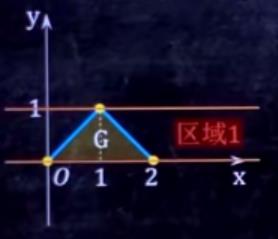
y的范围是区间。积分上限是右边线的y的表达式,下限是左边线的y的表达式。


答案:

接下来尝试自己做例2:

解:
对x:


对y:

已知两个边缘密度函数求f(x,y)
其实就是已知f(x),f(y)来求f(x,y)。
如题:
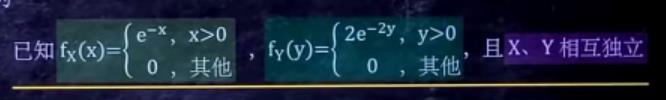
步骤:
把f(x),f(y)不为0的表达式相乘,范围加在一起即可(相互独立,可以同时满足)
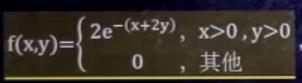
以上是关于已知权函数=1+x^2,区间服[负1,1],求首项系数为1的正交多项式,n=0,1,2,3,4的主要内容,如果未能解决你的问题,请参考以下文章