怎么用matlab求解非线性最优化问题

Posted 2023-05-13

参考技术A 在MATLAB的M文件编辑窗口中编入目标函数(obj_fun.m)以及非线性的约束条件（nl_con_fun.m）的M文件。在MATLAB的命令窗口中输入所需参数：A=[…];B=[…];Aeq=[…];Beq=[…]；LB；UB以及X0等。最后在命令窗口中输入命令：
[x,obj_value,EXITFLAG]=FMINCON('obj_fun',X0,A,B,Aeq,Beq,LB,UB,'nl_con_fun');
如果 (EXITFLAG<=0)，则原问题不可行或无解。如果 (EXITFLAG>0)，则x与obj_value分别为最优解和目标函数的最优值。 参考技术B 用粒子群算法，你直接把问题说出来吧。用非线性函数描述。 参考技术C 加qq说

单目标优化求解基于matlab非线性权重的自适应鲸鱼算法求解单目标优化问题(NWAWOA)含Matlab源码 1665期

一、非线性权重的自适应鲸鱼算法

随着现实生活中待优化问题的复杂度增加,种群优化算法得到迅速发展。目前,各种鲸鱼优化算法被提出,但是在不断提高精度的同时,却增加了算法的复杂性。针对鲸鱼优化算法（WOA）收敛速度慢、求解精度低的问题,在优化算法性能的基础上保留鲸鱼优化算法结构简单的特点,提出了基于非线性权重的自适应鲸鱼优化算法（NWAWOA）。通过非线性权重S1和S2对鲸鱼优化算法三个阶段的位置更新公式采用两种不同的加权策略,在平衡算法全局搜索与局部开发能力的同时,加快收敛速度、提高求解精度。在10个经典测试函数上的实验表明,改进的算法与经典粒子群算法（PSO）、WOA、WOAWC算法、EWOA算法相比具有较好的收敛速度、求解精度和稳定性,同时算法结构简单,易于学习。

1 自适应权重
鲸鱼优化算法与其他群体智能算法一样，平衡全局搜索和局部开发能力十分重要。权重对鲸鱼优化算法有重要作用，权重较大时，收敛速度较快，算法搜索的范围较大；权重较小时，搜索更加细致，不易错过最优解。

在鲸鱼优化算法中引入非线性权重S1和S2（如图1所示），分别对当前最优位置和包围步长进行自适应调整，具体计算公式如下：

其中，γ为S1和S2的变化范围取值，取γ=0.5；λ为S1和S2的取值步长，取λ=1。

图1 自适应权重S1和S2
将权重S1和S2引入到式（2）和式（5）中，如下所示：

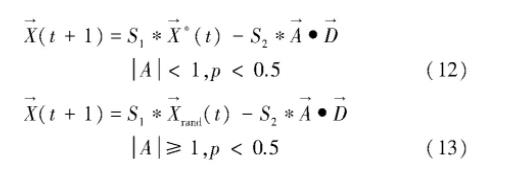
笔者认为将权重S1引入到位置上，不符合智能优化的初衷，改进公式如下：

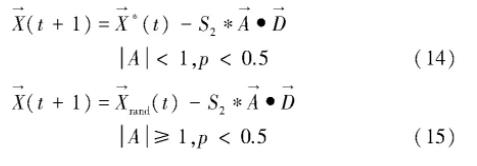
螺旋式位置更新公式即：

由图1可以看出，S1随迭代次数增加呈非线性递增，使种群能充分向最优位置移动；而S2随迭代次数增加呈非线性递减，在后期有较小步长而加快收敛速度。在平衡全局搜索和局部开发能力的同时，提高求解精度、加快收敛速度。

2 算法流程
改进的鲸鱼优化算法，对三个阶段的位置更新公式采取了不同的加权策略：在包围捕食和搜寻食物阶段，即p<0.5，非线性减小的权重S2仅对距离数据加权；在泡网攻击阶段的螺旋式更新位置，即p≥0.5，非线性增加的权重S1不仅对距离数据加权而且对位置加权。鲸鱼算法流程如图2所示。

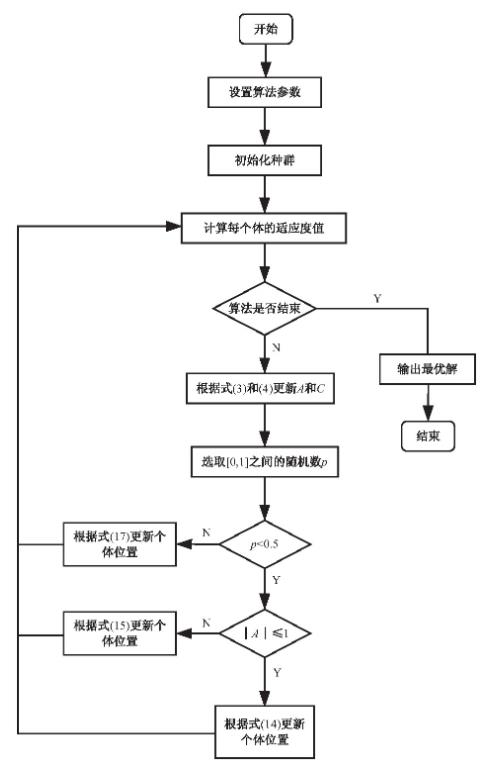
图2 NWAWOA算法流程

二、部分源代码

clear all 
clc
SearchAgents_no=30; % Number of search agents 种群数量
Function_name='F4'; % Name of the test function that can be from F1 to F23 (Table 1,2,3 in the paper) 设定适应度函数
Max_iteration=500; % Maximum numbef of iterations 设定最大迭代次数

% Load details of the selected benchmark function
[lb,ub,dim,fobj]=Get_Functions_details(Function_name);  %设定边界以及优化函数
%原始鲸鱼算法
[Best_score,Best_pos,WOA_cg_curve]=WOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj); %开始优化
%改进鲸鱼算法
[Best_score1,Best_pos1,WOA_cg_curve1]=NWAWOA(SearchAgents_no,Max_iteration,lb,ub,dim,fobj); %开始优化


figure('Position',[269   240   660   290])
%Draw search space
subplot(1,2,1);
func_plot(Function_name);
title('Parameter space')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])

%Draw objective space
subplot(1,2,2);
semilogy(WOA_cg_curve,'Color','g','linewidth',1.5)
hold on
semilogy(WOA_cg_curve1,'Color','r','linewidth',1.5);
title('Objective space')
xlabel('Iteration');
ylabel('Best score obtained so far');
legend('WOA','NWAWOA');
axis tight
grid on
box on
display(['The best solution obtained by WOA is : ', num2str(Best_pos)]);
display(['The best optimal value of the objective funciton found by WOA is : ', num2str(Best_score)]);

        
display(['The best solution obtained by NWAWOA is : ', num2str(Best_pos1)]);
display(['The best optimal value of the objective funciton found by NWAWOA is : ', num2str(Best_score1)]);

三、运行结果

四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例（第2版）[M].电子工业出版社，2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社，2017.
[3]赵传武,黄宝柱,阎跃观,代文晨,张建.一种非线性权重的自适应鲸鱼优化算法[J].计算机技术与发展,2020,30(10):7-13.