TreeMap和TreeSet即Java中利用二叉搜索树实现的Map和Set

Posted 2020-11-28

一：概念
二叉搜索树又称二叉排序树，它或者是一棵空树**，或者是具有以下性质的二叉树:
若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树。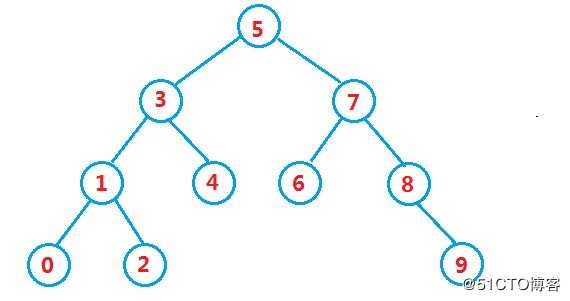

二：操作——查找
先和根节点做对比，相等返回，如果不相等，
关键码key>根节点key,在右子树中找(root=root.rightChild)
关键码key<根节点key,在左子树中找(root=root.leftChild)
否则返回false

三：操作——插入
根据二叉排序树的性质，左孩子比根节点的值小，右孩子比根节点的值大。关键码key先于根节点key作比较，然后再判断与根节点的左或者右作比较，满足二叉排序树性质时，即为合理位置，然后插入。

四： 操作-删除（难点）
设待删除结点为 cur, 待删除结点的双亲结点为 parent
1. cur.left == null

1. cur 是 root，则 root = cur.right
2. cur 不是 root，cur 是 parent.left，则 parent.left = cur.right
3. cur 不是 root，cur 是 parent.right，则 parent.right = cur.right
   2. cur.right == null
4. cur 是 root，则 root = cur.left
5. cur 不是 root，cur 是 parent.left，则 parent.left = cur.left
6. cur 不是 root，cur 是 parent.right，则 parent.right = cur.left
   3. cur.left != null && cur.right != null
7. 需要使用替换法进行删除，即在它的右子树中寻找中序下的第一个结点(关键码最小)，用它的值填补到被删除节点中，再来处理该结点的删除问题

五：实现

public class BinarySearchTree<K extends Comparable<K>, V>
{ 
public static class Node<K extends Comparable<K>, V> 
{
K key; 
V value; 
Node<K, V> left;
Node<K, V> right;

public String toString()
{ 
return String.format("{%s, %s}", key, value);
}
}
private Node<K, V> root = null;
public V get(K key) 
{ 
Node<K, V> parent = null; 
Node<K, V> cur = root; 
while (cur != null)
{ 
parent = cur;
int r = key.compareTo(cur.key);
if (r == 0)
{ 
return cur.value;
} 
else if (r < 0) {
cur = cur.left; 
}

else 
{
cur = cur.right;
} 
}
return null; 
}
public V put(K key, V value)

{ 
if (root == null)
{ root = new Node<>();
root.key = key;
root.v
display(root);
return null;
}
Node<K, V> parent = null; 
Node<K, V> cur = root; 
while (cur != null) 
{ 
parent = cur;

int r = key.compareTo(cur.key);
if (r == 0) 
{ 
V oldValue = cur.value; 
cur.value = value; 
display(root); 
return oldValue; 
}
else if (r < 0)
{ 
cur = cur.left; 
} 
else

{ 
cur = cur.right;
} 
}
Node<K, V> node = new Node<>(); 
node.key = key; 
node.value = value;
int r = key.compareTo(parent.key);
if (r < 0)
{ parent.left = node;
} 
else { parent.right = node; 
}
display(root); 
return null; 
}
public V remove(K key) 
{ 

Node<K, V> parent = null; 
Node<K, V> cur = root; 
while (cur != null) 
{ 
int r = key.compareTo(cur.key);
if (r == 0)
{ 
V oldValue = cur.value; 
deleteNode(parent, cur);
display(root); 
return oldValue; } 
else if (r < 0)
{ parent = cur; cur = cur.left; }
else { parent = cur; cur = cur.right; 
} 
}
display(root); 
return null;
}
private void deleteNode(Node<K,V> parent, Node<K,V> cur) 
{
if (cur.left == null)
{
if (cur == root)
{
root = cur.right;
} 
else if (cur == parent.left)
{ parent.left = cur.right; }
else { parent.right = cur.right; }
} else if (cur.right == null)
{ 
if (cur == root)
{ root = cur.left; }
else if (cur == parent.left)
{ parent.left = cur.left; }
else { parent.right = cur.left; }
} else {
// 去 cur 的右子树中寻找最小的 key 所在的结点 scapegoat
// 即 scapegoat.left == null 的结点
Node<K,V> goatParent = cur;
Node<K,V> scapegoat = cur.right;
while (scapegoat.left != null)
{ goatParent = scapegoat; scapegoat = cur.left; }
cur.key = scapegoat.key;
cur.value = scapegoat.value;
if (scapegoat == goatParent.left)
{
goatParent.left = scapegoat.right;
}
else { goatParent.right = scapegoat.right; }
} 
}
private static <K extends Comparable<K>,V> void display(Node<K,V> node) 
{
System.out.print("前序: ");
preOrder(node);

System.out.println();
System.out.print("中序: ")
inOrder(node); 
System.out.println(); }
private static <K extends Comparable<K>,V> void preOrder(Node<K,V> node)
{ if (node == null)
{ return; }
System.out.print(node + " ");
preOrder(node.left);
preOrder(node.right); }
private static <K extends Comparable<K>,V> void inOrder(Node<K,V> node)
{ if (node == null) 
{ return; }
inOrder(node.left);
System.out.print(node + " ");
inOrder(node.right); }
public static void main(String[] args)
{ 
BinarySearchTree<Integer, String> tree = new BinarySearchTree<>(); 
int[] keys = { 5, 3, 7, 4, 2, 6, 1, 9, 8 }; 
for (int key : keys) 
{
tree.put(key, String.valueOf(key)); }
System.out.println("=================================="); tree.put(3, "修改过的 3"); System.out.println("=================================="); tree.remove(9);
tree.remove(1); t
ree.remove(3);
``` } 
}

**六：性能分析**
插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。
但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树。
**七： 和 java 类集的关系**
TreeMap 和 TreeSet 即 java 中利用搜索树实现的 Map 和 Set；