spss描述性分析

Posted 2023-05-09

你好
一、描述性统计分析

概念：是以概括性数据描述数据特征的各项活动。

通俗的讲就是用儿子代表全家

集中趋势：关于数据“中心位置”的某种表述，也就是常说的“平均起来”

常见的有均数、中位数等

离散趋势：反应数据的波动范围大小

常见的有标准差、方差、四分位数

分布特征：数据的分布应该满足某种特征，比如正态分布

衍生出一系列概念描述数据与正态分布之间的关系，比如偏度系数以及封度系数

二、集中趋势描述指标

算数平均数：使用一个数高度浓缩数据，也就是说平均数是描述一组数到一个数的距离。

使用范围：定距变量，单峰（如上图）或者基本对称的情况下才适用使用平均数。也就是说

均数适用于正态分布（包含极值的称为偏态分布）。在正态分布中均值代表集中趋势。

中位数:是一种位置平均数，将整体各单位按照大小排序，取中间位置的数

捷尾均数：去掉极值之后的均数

三、离散趋势描述指标

极差：最大值与最小值之差。反应数据的离散幅度，或者变异范围。

局限：取决于极端情况：1、不能反应数据分布情况

2、受极端值影响较大，不符合数据稳健性要求

适用于大体上了解数据的波动情况。

方差和标准差：

本质上反应数据与均值的差异情况。这种差异称为离散也称变异。

方差与标准差只适用于正态分布（无极端值）

分位数：

分位数本质上反应的是缩小极端值对变异幅度的影响。

适用范围：样本足够多。只是人为的切割，并非通过计算得出，不如均值和标准差精准。但是

中间位置原理极值，样本稳定。

变异系数:

是标准差与平均数的比值。

本质上是消除数据大小差异（平均数）后的波动情况（标准差）

四、连续变量的参数估计

正态分布：

是关于均值对称的分布，均值处为最大值。同时标准差（个体差异）影响曲线的形态（矮阔尖峭）

偏度：描述分布不对称的方向和程度。

尾巴所在的方向为分布方向

峰度：描述曲线的陡峭程度

标准正态分布：标准差为1，关于0对称

如果偏度系数标准差/峰度系数标准差>2说明不服从正态分布。

五、spss的实现

tvg指偏度系数标准差，利润范围指峰度系数标准差。 参考技术A

一、数据处理

1、数据变量

数据类型主要为字符型、数值型和日期型三种。

2、变量尺度

即变量的度量标准。主要为名义（N）——分类变量、度量（S）——连续变量。

3、数据清洗

删除重复项：

利用【数据】→【标识重复个案】→将所有变量放入【定义匹配个案的依据】→【确定】

结果中0代表重复个案，1为唯一个案，升序排列，删除最后一个基本个案值为0的项，重复项就删除了。

4、数据抽取

4.1、字段拆分

打开数据文件→【转换】→【计算变量】→【函数组】→【字符串】→【CHAR.SUBSTR(3)函数】→新建【目标变量】→填写【字符串表达式】→【确定】该函数有三个参数CHAR.SUBSTR（字符串表达式，位置，长度）例如：

CHAR.SUBSTR(‘abcd’,2,2)返回“bc”

4.2、随机抽样

打开文件→【数据】→【选择个案】→【随机个案样本】→【样本】→输入选择随机样本数，可以输入20%的所有个案。

5、数据合并

5.1、字段合并

打开文件→【转换】→【计算变量】→【函数组】→【字符串】→【CONCAT函数】→填写【字符串表达式】→新建【目标变量】→【确定】

Concat（strexpr,strexpr2,,,,,）例如concat（年，“-”，月，“-“，日）strexpr是字符串变量。

5.2、记录合并

打开文件→【数据】→【合并文件】→【添加个案】→【外部SPSS Statistics数据文件】→选择文件→继续→确定

6、数据分组

6.1、可视分箱

打开文件→【转换】→【可视离散化】→【要离散的变量】→选择要离散化的变量→【继续】→命名【离散的变量】→点击【生成分割点】→填写【第一个分割点位置】、【分割点数】、【宽度】→【应用】→【生成标签】→【确定】

6.2、重新编码

打开文件→【转换】→【重新编码为不同变量】→选择【输入变量】→命名【输出变量】→【更改】→【旧值和新值】→【旧值】→【范围】→【新值】→【添加】→【确定】

7、数据标准化

7.1、0-1标准化

对原始数据进行线性变换，使结果落到【0，1】区间。

公式为

X^=x-min/max-min

打开文件→【转换】→【计算变量】→【数字表达式】框中输入公式→命名【目标变量】为标准化值→【类型与标签】→【数值】→【继续】→【确定】

7.2、Z标准化

将变量中的测量值处理成服从标准正态分布的数据值，即均值μ为0，标准差σ为1。

X^=（x-μ）/σ

打开文件→【分析】→【描述统计】→【描述】→选择变量→勾选【将标准化值另存为变量】→【确定】

二、描述性分析

1、频率分析

1.1 分类变量频率分析

打开文件→【分析】→【描述统计】→【频率】→选择要进行频率分析的变量到【变量】→【确定】

1.2 打开文件→【分析】→【描述统计】→【频率】→选择要进行频率分析的变量到【变量】→点击【统计量】选择想要输出的统计量→【继续】→点击【图表】按钮→选择【直方图】勾选【在直方图中显示正态曲线】→勾选【显示频率表】→【确定】

2、描述分析

【分析】→【描述统计】→【描述】→选择变量→【选项】→选择需要输出的统计量→【继续】→【确定】

3、交叉表分析

【分析】→【描述统计】→【交叉表】→选择行变量、列变量→【单元格】选择输出格式，可以勾选【百分比】→【继续】→【确定】

4、数据报表制作

【分析】→【表】→【设定表】→选择变量到行或者列→【摘要统计量】选择想要添加的其他统计量（比如列数N%）→【分类和总计】添加小计/总计→【应用选择】→【确定】

还有不明白的也可以去SPSS中文官网看看。

SPSS——描述性统计分析——探索性分析

菜单

除了可以计算基本的统计量之外，也可以给出一些简单的检验结果和图形，有助于用户进一步的分析数据。使得用户能够从大量的分析结果之中挖掘到所需要的统计信息。

适用范围
对资料的性质、分布特点等完全不清楚的时候

Analyze -> Descriptive Statistics -> Expore

数据源

ceramics.sav

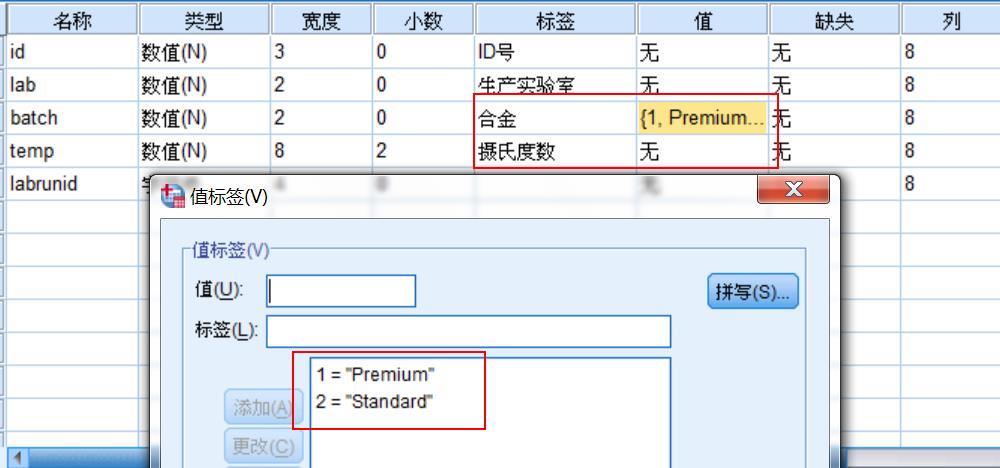
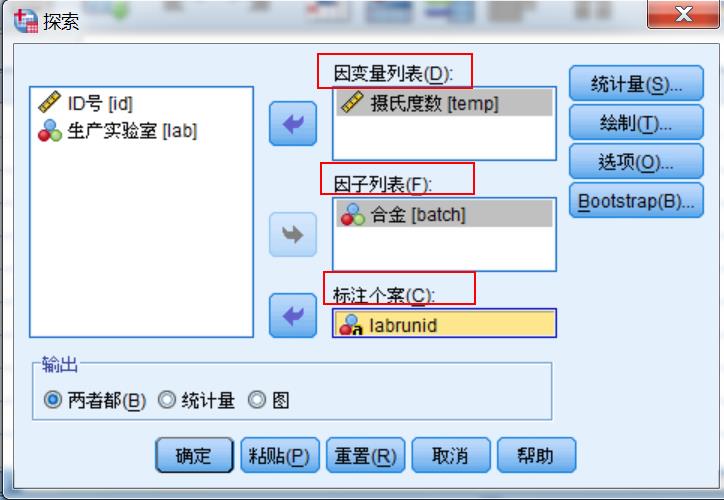
• 因变量列表
  用于选入待分析的变量
• 因子列表
  用于选择分组变量，根据该变量取值不同，分组分析因变量列表中的变量
• 标注个案
  选择标签变量

统计量

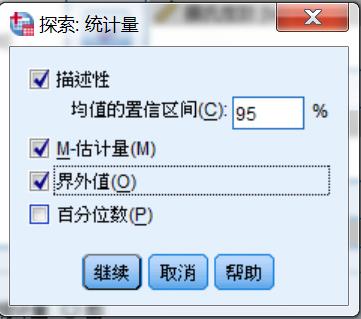
• 描述性
  计算一般的描述性统计量，及指定的均数可信区间
• M-估计量
  描述集中趋势的统计量，用于稳健估计
• 界外值
  分别输出5个极大值和极小值
• 百分位数
  输出变量5%,10%,25%,50%,75%,90%,95%分位数

绘制

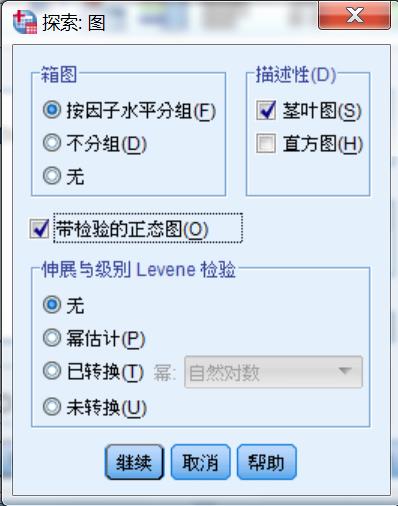
• 带校验的正态图
  选择是否进行正态校验，且是否输出相应的Q-Q图
• 伸展与级别Levene检验
  当选入分组变量时，该功能才被激活，主要用于比较各组之间的离散程度是否一致。在这里可以选择“未转换”，用于方差齐性检验

选项

输出结果

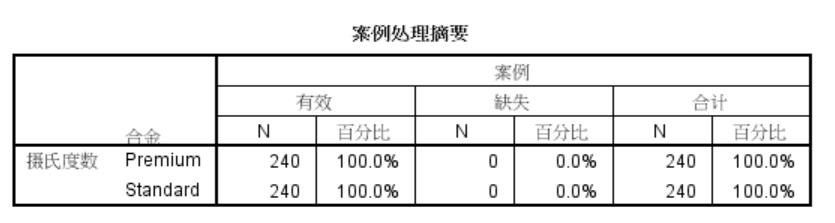
个案处理分析结果

包括观测量、缺失值等信息

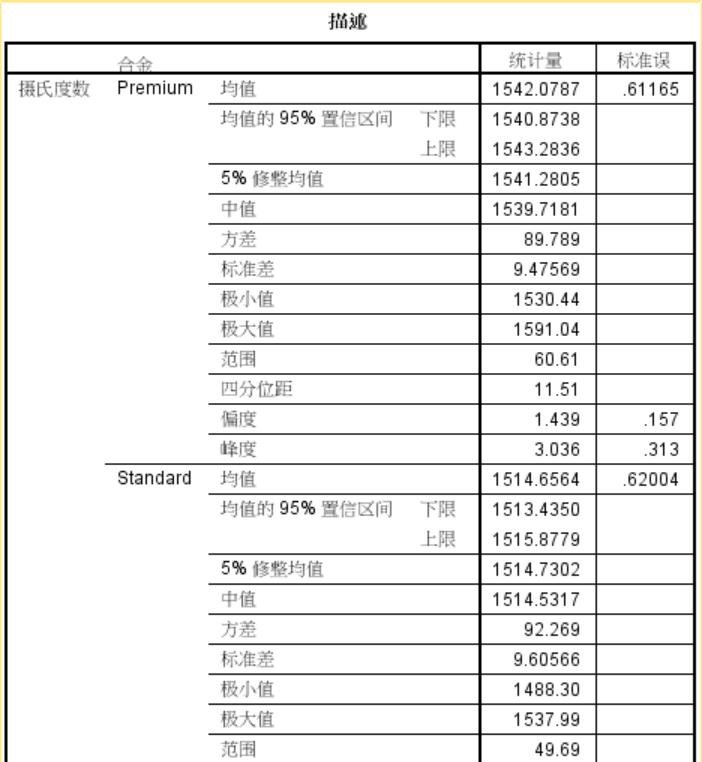
描述性统计量

包括：均值、95%置信区间、方差、中位数、标准差、最大最小值、偏度和峰度等信息

集中趋势分布的3种较佳平稳测度

• 较佳测度之一：中位数等

  • 中位数
    与均值和众数大不相同，中位数是依赖于数据的主体部分而不是极值，因此它的值不是过分地受某几个观察值的影响
  • 平稳估计量
    如果对数据来源的总体做出某个假设（比如假定服从正态分布），则会有更佳分布位置的估计量，这种估计量称为平稳或稳健测度的估计量

• 较佳测度之二：修正均值
  由于均值深受极端值影响，因此可通过去掉一些远离主体数据的极端值，进而获得一个对于分布位置简单而平稳的估计量

  • 5%修正均值
    是通过去掉所有观察值中最大的5%和最小的5%的数据而获得
    调整后的均值与中位数可更好的利用数据

• 较佳测度之三：M估计
  将极端值计算在内，而赋予比靠近中央值较小的一个权重，这种方法可借助M估计或采用广义最大似然估计
  M-estimators：平稳分布位置的最大似然估计量

  • Huber的M估计值
  • Tukey双权重估计值
  • Hampel重复递减M估计值
  • Andrew波形估计值

M-估计器

极值

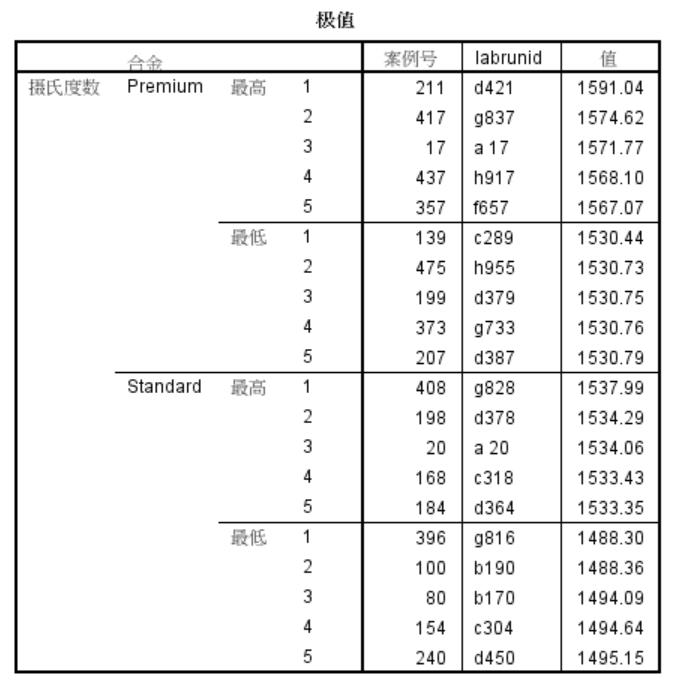
这里用标注个案来标记极值

正态性检验

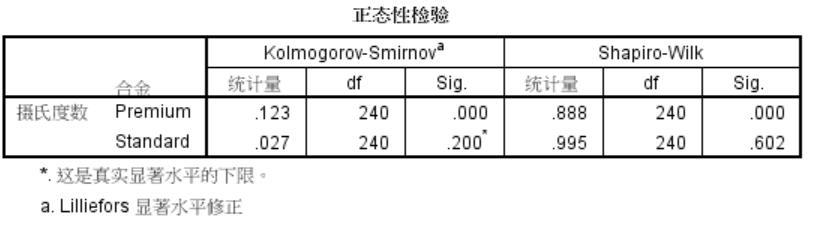
• 其中Premium变量对应的K-S检验P值和Shapiro-Wilk检验P值均为0.000，非常显著，应该拒绝原假设。所以，此变量的数据分布不是正态分布。
• 而Standard数据的分布不是显著的，可以认为是正态分布

在‘探索’里出现的Kolmogorov-Smirnov 检验，它的右上角有一个a 的注释号。它将Kolmogorov-Smirnov 检验改进用于一般的正态性检验。

而在‘非参数检验’里出现的Kolmogorov-Smirnov 检验，是没有经过纠正或改进的。

该正态性检验只能做标准正态检验。

 SPSS 规定：当样本含量3≤n≤5000 时，结果以Shapiro—Wilk(W 检验)为难，当样本含量n>5000 结果 以Kolmogorm —Smimov(D检验)为准。

问题：

(1) 在实际应用中常出现检验结果与直方图、正态性概率图不一致，甚至几种假设检验方法结果完全不同的情况。

(2) Shapiro—Wilk 检验(Ⅳ 检验)和经过Lilliefors 显著水平修正的Kolmogorov—Smirnov 检验(D 检验)是用 一个综合指标(顺序统计量Ⅳ 或D)来判定资料的正态性由于两种方法都是用一个指标反映资料的正态性，

所以当资料的正态峰和对称性两个特征有一个不满足正态性要求时，两种方法出现假阴性错误的机率均较 大；而且两种方法的检验统计量都是进行大小排序后得到，所以易受异常值的影响。

(3) Kolmogorov—Smirnov 单一样本检验是根据实际的累计频数分布和理论的累计频数分布的最大差异来检验资料的正态性，可对正态分布进行拟合优度检验。但它并非检验正态性的专用方法，因此它的检验效率是最低的，最容易受样本量和异常值等因素的影响。

方差齐性检验

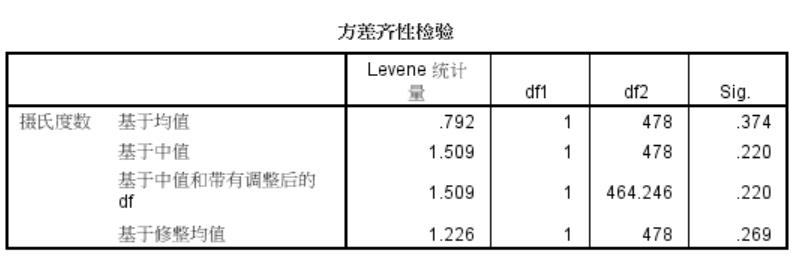
假设检验：
H0: 两样本方差齐性（相等，或无显著性差异）

如上图，Sig > 0.2，并无显著差异。

正态Q-Q图

正态性检验可以通过直观的Q-Q图，进行人工验证。

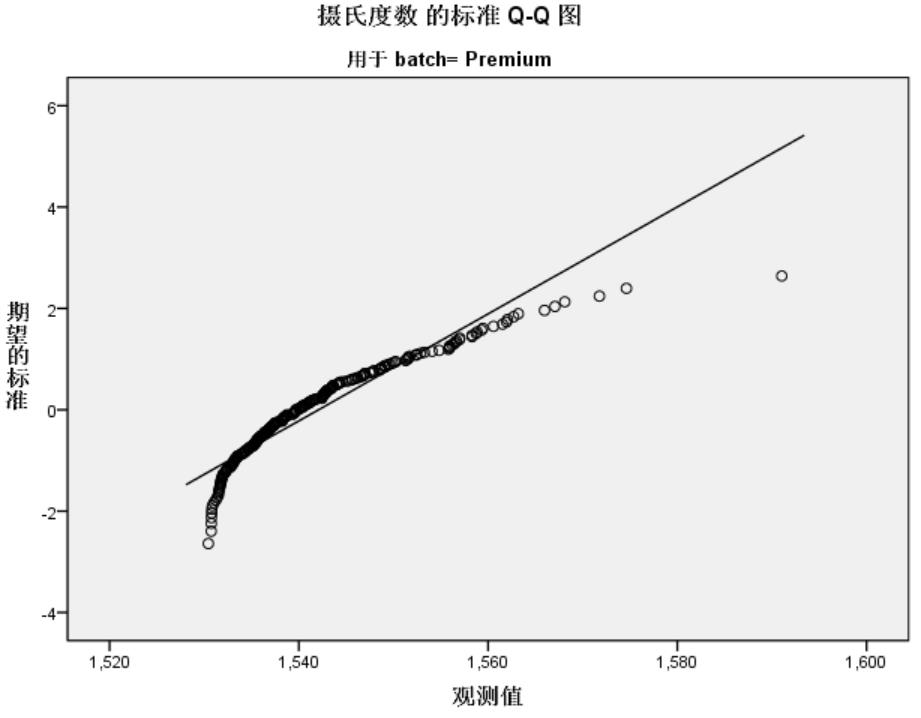
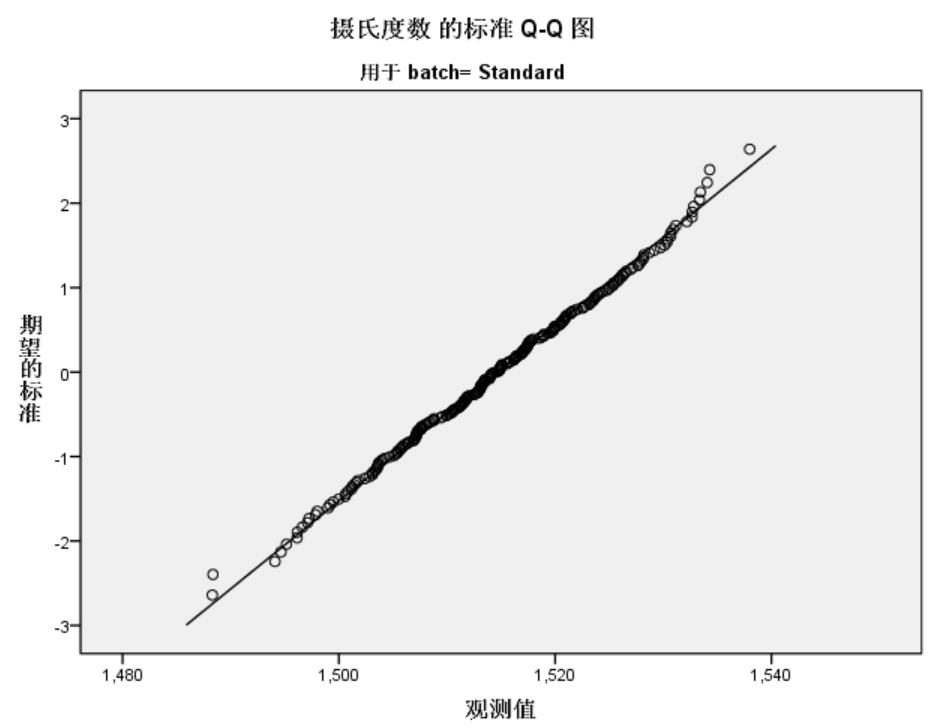
Q-Q图是一种散点图,对应于正态分布的Q-Q图,就是由标准正态分布的分位数为横坐标,样本值为纵坐标的散点图. 要利用QQ图鉴别样本数据是否近似于正态分布,只需看QQ图上的点是否近似地在一条直线附近,而且该直线的斜率为标准差,截距为均值.

如上图，batch=Standard Q-Q图上的点在一条直线附近，可以认为是正态分布，和正态性检验Lilliefors，Shapiro-Wilk得出的结果一致。

反趋势正态 Q-Q 图

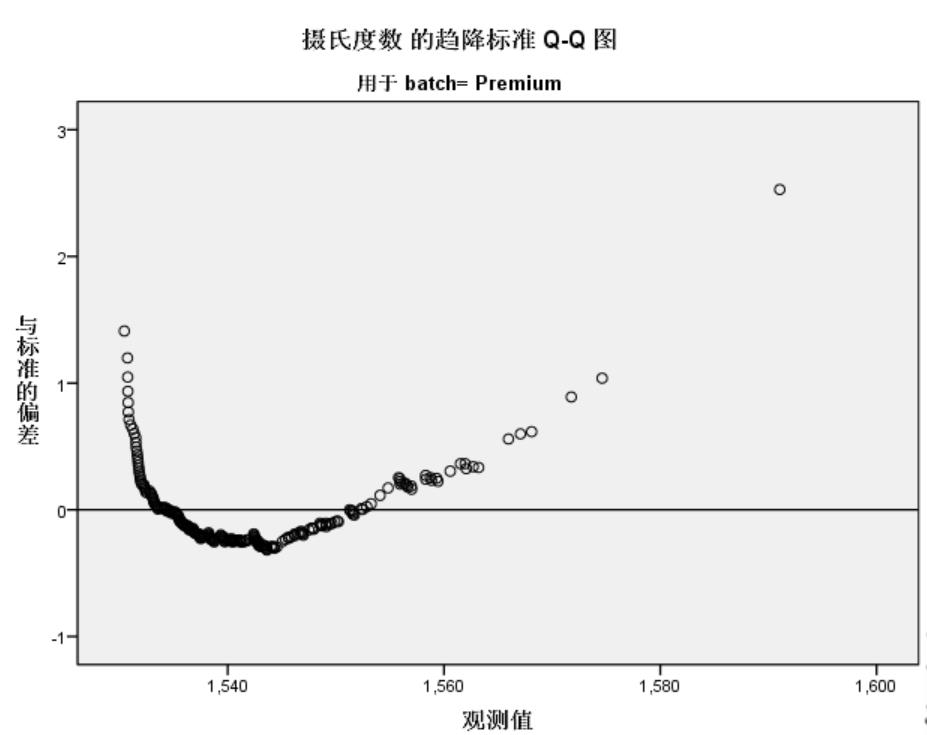
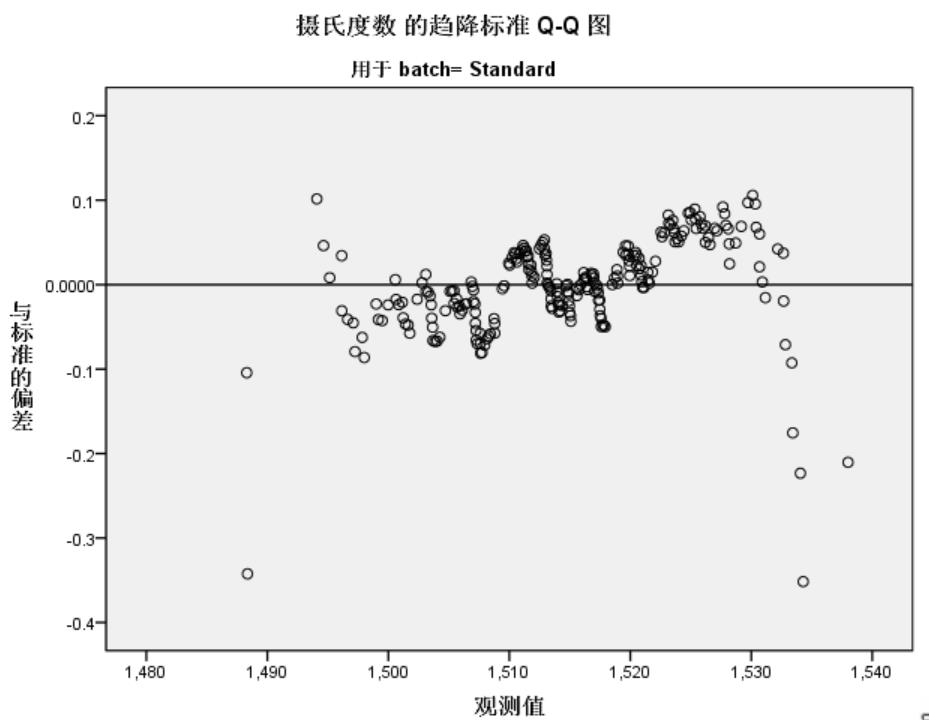
如上图，反趋势正态概率Q-Q图以变量的观测值为X坐标，以变量的Z得分与期望值的偏差为Y坐标。
batch=Standard 图的观测点离期望值很集中，说明符合正态分布。

盒子图

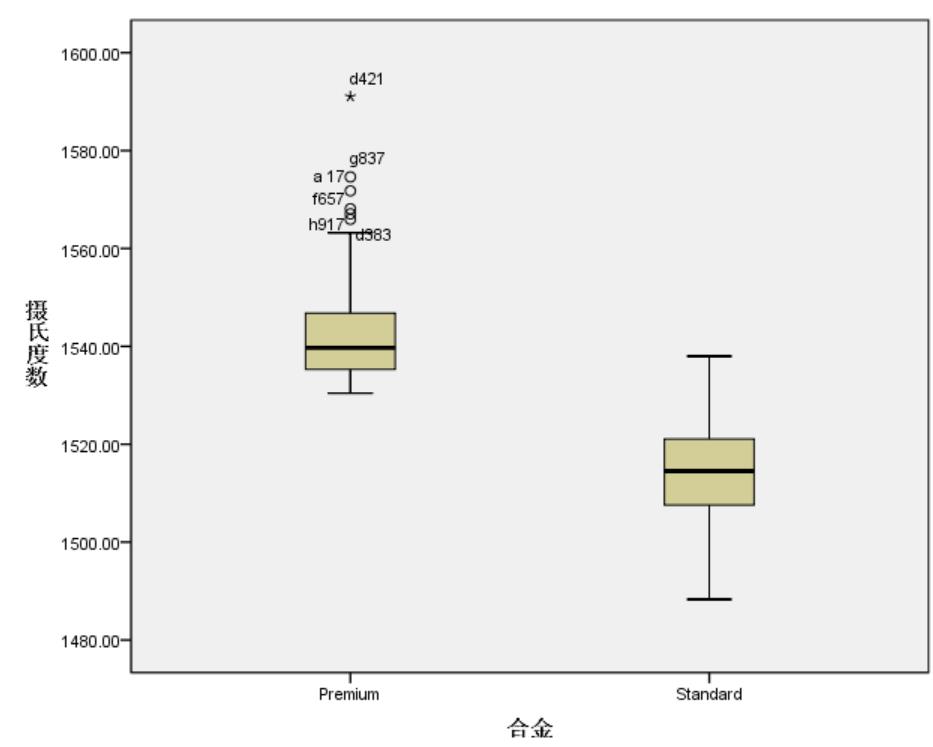
Premiun中有部分异常数据，数据偏大。需要进行异常值检测。