80坐标系与54坐标系的鉴别？

Posted 2023-05-08

参考技术A

1、80坐标的中央子午线是114，不同的是，54坐标的中央子午线是118.3。

2、80坐标系是参心坐标系，不同的是，54坐标系为参心大地坐标系。

3、80坐标系的大地原点设在我国中部的陕西省泾阳县永乐镇，不同的是，54坐标系大地原点在原苏联的普尔科沃。

西安80坐标系与北京54坐标系其实是一种椭球参数的转换作为这种转换在同一个椭球里的转换都是严密的，而在不同的椭球之间的转换是不严密，因此不存在一套转换参数可以全国通用的，在每个地方会不一样，因为它们是两个不同的椭球基准。

北京54和西安80是两种不同的大地基准面，不同的参考椭球体，因而两种地图下，同一个点的坐标是不同的，无论是三度带六度带坐标还是经纬度坐标都是不同的。

扩展资料

北京54坐标系特点

1、属参心大地坐标系。

2、采用克拉索夫斯基椭球的两个几何参数。

3、大地原点在原苏联的普尔科沃。

4、采用多点定位法进行椭球定位。

5、高程基准为 1954年青岛验潮站求出的黄海平均海水面。

6、高程异常以原苏联 1955年大地水准面重新平差结果为起算数据。按我国天文水准路线推算而得。

参考资料：百度百科——西安80坐标系

参考资料：百度百科——北京54坐标系

大地经纬度坐标系与Web墨卡托坐标系的转换

详细论述了大地经纬度坐标系与Web墨卡托坐标系的转换的原理与实现。

目录

• 1. 概述
• 2. 实现
• 3. 参考

1. 概述

我在《大地经纬度坐标与地心地固坐标的的转换》这篇文章中已经论述了大地坐标系/地理坐标系的概念，简单来说就是由经度、纬度以及高程（BLH）确定的坐标系，它是一种曲面坐标。

然而，在实际使用过程中我们用的最多的还是平面坐标，并且单位最好与常用的长度单位（米）一致。所以就产生了从曲面到平面的转换，这个过程也叫做投影，转换的结果也就是投影平面坐标系。我在《GDAL坐标转换》这篇文章中详细论述了我们国内常用的三种投影平面坐标系：横轴墨卡托投影，高斯-克吕格投影和UTM投影。本质上来说，高斯-克吕格投影和UTM投影其实都是横轴墨卡托投影，横轴墨卡托投影也是用的最为广泛的地图投影方式。

但是在GIS，尤其是WebGIS领域中，横轴墨卡托投影的使用远没有Web墨卡托投影方式用的多。最重要的原因是Web墨卡托投影的转换算法比横轴墨卡托投影要简单很多，符合Web的轻量化的特点。

2. 实现

Web墨卡托投影是横轴墨卡托投影的特化版，要完全搞清楚Web墨卡托投影就必须得先搞清楚横轴墨卡托投影，不过横轴墨卡托投影实在太复杂了，但是我们可以定性地去理解。它的计算过程大概可以这样理解：

在X方向上，为了保证投影到平面后经线和纬线仍然垂直，那么每条纬线都会按照赤道周长展开，也就是\\(2*PI*r = 2*20037508.3427892\\)。由于原点位于平面中心，那么可以算得X轴的取值范围：[-20037508.3427892,20037508.3427892]。经度与投影后X长是简单的线性关系。

在Y方向上，则需要借助于墨卡托投影公式。为了保证投影的结果是正方形，那么就把Y轴的取值范围也取值成[-20037508.3427892,20037508.3427892]之间。这样做没什么道理，纯粹是为了希望投影的结果是正方形，便于切片。最后，通过墨卡托投影公式进行反算，得到的经纬度范围就是[-85.05112877980659，85.05112877980659]。也就是这种投影方式，大于这个范围是失效的。

参考Cesium的具体实现如下：

#include <iostream>
//#include <eigen3/Eigen/Eigen>

//#include <osgEarth/GeoData>

using namespace std;

const double epsilon = 0.000000000000001;
const double pi = 3.14159265358979323846;
const double d2r = pi / 180;
const double r2d = 180 / pi;

const double a = 6378137.0;		//椭球长半轴
const double f_inverse = 298.257223563;			//扁率倒数
const double b = a - a / f_inverse;
//const double b = 6356752.314245;			//椭球短半轴

const double e = sqrt(a * a - b * b) / a;

//墨卡托范围[-PI, PI]->大地纬度范围[-PI/2, PI/2]
static double mercatorAngleToGeodeticLatitude(double mercatorAngle)
{
	return pi / 2.0 - (2.0 * atan(exp(-mercatorAngle)));
	//return 2.0 * atan(exp(mercatorAngle)) - pi / 2.0;
}

//Web墨卡托投影所支持的最大纬度（北和南）
static double maximumLatitude = mercatorAngleToGeodeticLatitude(pi);

//大地纬度范围[-PI/2, PI/2]->墨卡托范围[-PI, PI]
static double geodeticLatitudeToMercatorAngle(double latitude)
{
	// Clamp the latitude coordinate to the valid Mercator bounds.
	if (latitude > maximumLatitude)
	{
		latitude = maximumLatitude;
	}
	else if (latitude < -maximumLatitude)
	{
		latitude = -maximumLatitude;
	}
	double sinLatitude = sin(latitude);
	return 0.5 * log((1.0 + sinLatitude) / (1.0 - sinLatitude));
} 

void Blh2Wmc(double &x, double &y, double &z)
{
	x = x * d2r * a;
	y = geodeticLatitudeToMercatorAngle(y * d2r) * a;
}

void Wmc2Blh(double &x, double &y, double &z)
{
	//var oneOverEarthSemimajorAxis = this._oneOverSemimajorAxis;
	x = x / a * r2d;
	y = mercatorAngleToGeodeticLatitude(y / a) * r2d;	
}

int main()
{
	double x = 113.6;
	double y = 38.8;
	double z = 100;	   

	printf("%.10lf\\n", maximumLatitude * r2d);

	printf("原大地经纬度坐标：%.10lf\\t%.10lf\\t%.10lf\\n", x, y, z);
	Blh2Wmc(x, y, z);
	printf("Web墨卡托坐标：%.10lf\\t%.10lf\\t%.10lf\\n", x, y, z);
	Wmc2Blh(x, y, z);
	printf("转回大地经纬度坐标：%.10lf\\t%.10lf\\t%.10lf\\n", x, y, z);
}

最终运行的结果：

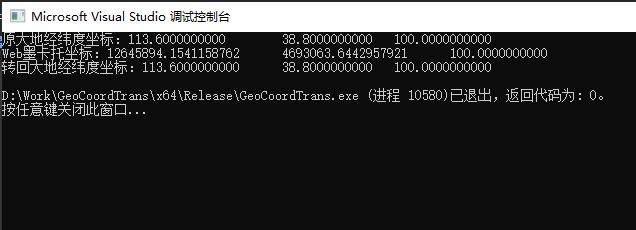
通过GlobalMapper中的坐标转换工具对照的结果如下：

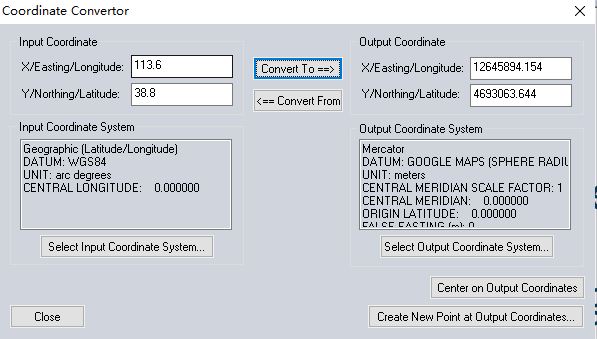
两者结果基本一致。

3. 参考

1. Web Mercator 公开的小秘密
2. GIS——各大地图厂商为什么偏爱web墨卡托投影
3. 墨卡托及Web墨卡托投影