java数据结构03

Posted 2020-11-25 心默默言

1.动态规划

如果使用上面的递归函数进行计算，会导致如下的重复计算：

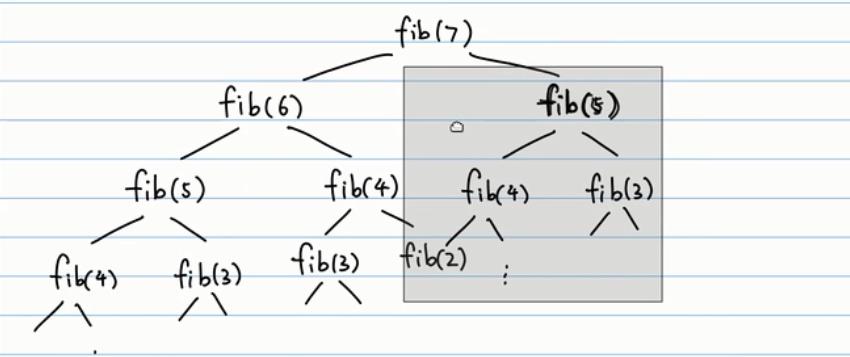
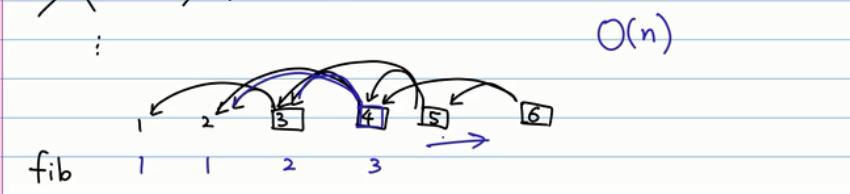
示例：

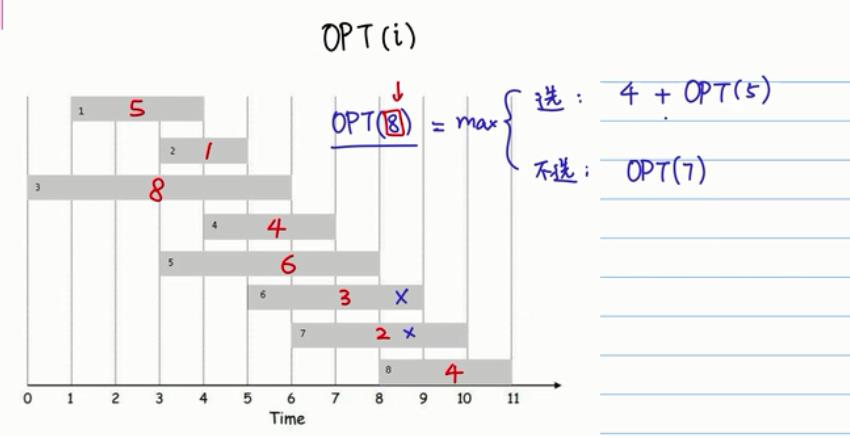
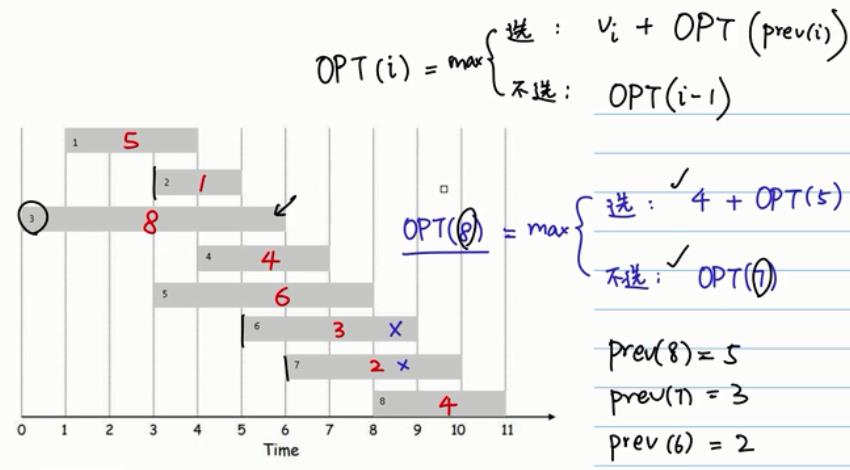
1.1实战示例1

从一个列表中选出一堆（若干）不相邻的数字，使这些数字相加的和最大。

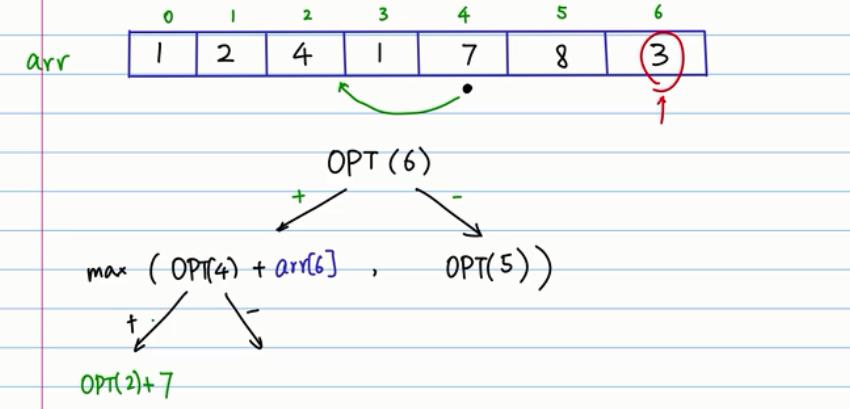
package datastruct.t05dynamic_programming;

public class DynamicProgramming {
    /**
     * 递归方式
     * 
     * @param arr：数组
     * @param i：第i个位置
     * @return
     */
    public static int recOpt(int[] arr, int i) {
        if (i == 0)
            return arr[0];
        if (i == 1)
            return Math.max(arr[0], arr[1]);
        else {
            int A = recOpt(arr, i - 2) + arr[i];
            int B = recOpt(arr, i - 1);
            return Math.max(A, B);
        }
    }

    /**
     * 非递归的方式
     */
    public static int dpOpt(int[] arr) {
        int[] opt = new int[arr.length];
        opt[0] = arr[0];
        opt[1] = Math.max(arr[0], arr[1]);
        for (int i = 2; i < arr.length; i++) {
            int A = opt[i - 2] + arr[i];
            int B = opt[i - 1];
            opt[i] = Math.max(A, B);
        }
        return opt[arr.length - 1];
    }

    public static void main(String[] args) {
        int[] arr = { 1, 2, 4, 1, 7, 8, 3 };
        int res = recOpt(arr, arr.length - 1);
        System.out.println(res);
        int res2 = dpOpt(arr);
        System.out.println(res2);
    }

}

1.2实战示例2

从某一数组里找出两个数字的和正好等于给定的数字，如果存在返回true，不存在返回false。

package datastruct.t05dynamic_programming;

public class Subset {
    /**
     * 递归的方式实现
     */
    public static boolean recSubset(int[] arr, int i, int target) {
        if (target == 0) {
            return true;
        } else if (i == 0) {
            return arr[0] == target;
        } else if (arr[i] > target) {
            return recSubset(arr, i - 1, target);
        } else {
            boolean A = recSubset(arr, i - 1, target - arr[i]);
            boolean B = recSubset(arr, i - 1, target);
            return A || B;
        }
    }

    public static void main(String[] args) {
        int[] arr = { 3, 34, 4, 12, 5, 2 };
        int target1 = 9;
        int target2 = 10;
        int target3 = 13;
        boolean res1 = recSubset(arr, arr.length - 1, target1);
        boolean res2 = recSubset(arr, arr.length - 1, target2);
        boolean res3 = recSubset(arr, arr.length - 1, target3);
        System.out.println(res1);
        System.out.println(res2);
        System.out.println(res3);
    }

}

package datastruct.t05dynamic_programming;

public class Subset {

    /**
     * 非递归方式实现
     */
    public static boolean dpSubset(int[] arr, int target) {
        boolean[][] subset = new boolean[arr.length][target + 1];
        // 所有行，第0列
        for (int i = 0; i < subset.length; i++) {
            subset[i][0] = true;
        }
        // 第0行，所有列
        for (int j = 0; j < subset[0].length; j++) {
            subset[0][j] = false;
        }
        subset[0][arr[0]] = true;
        
        for (int i = 1; i < subset.length; i++) {
            for (int s = 1; s < subset[0].length; s++) {
                if (arr[i] > s) {
                    subset[i][s] = subset[i - 1][s];
                } else {
                    boolean A = subset[i - 1][s - arr[i]];
                    boolean B = subset[i - 1][s];
                    subset[i][s] = A || B;
                }
            }
        }
        return subset[subset.length-1][subset[0].length-1];
    }

    public static void main(String[] args) {
        int[] arr = { 3, 34, 4, 12, 5, 2 };
        int target1 = 9;
        int target2 = 10;
        int target3 = 13;
    
        boolean res4 = dpSubset(arr, target1);
        boolean res5 = dpSubset(arr, target2);
        boolean res6 = dpSubset(arr, target3);
        System.out.println(res4);
        System.out.println(res5);
        System.out.println(res6);
    }

}

1.3DP01背包

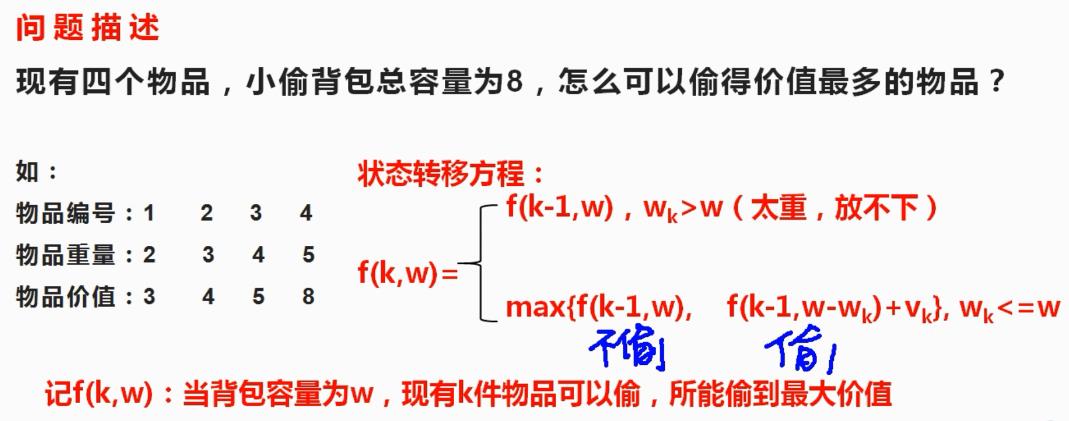
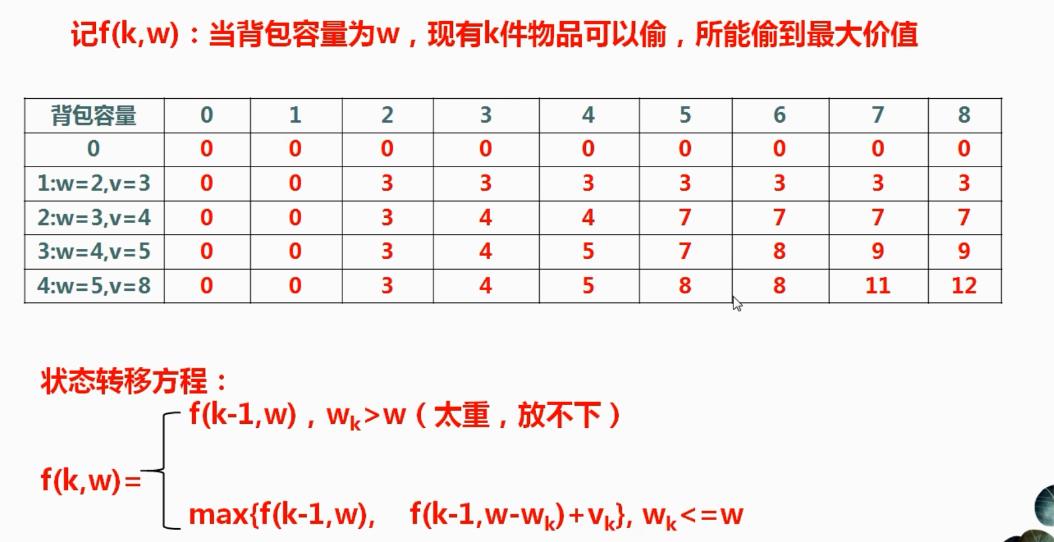
package datastruct.t05dynamic_programming;

import java.util.Scanner;

public class T01package {

    public static void main(String[] args) {
        //    int[] w = { 2, 3, 4, 5 };
        //    int[] v = { 3, 4, 5, 8 };
        Scanner input = new Scanner(System.in);
        String str1 = input.nextLine();
        String[] temp = str1.split(" ");//以空格拆分字符串
        int[] w = new int[temp.length];//int类型数组
        for (int i = 0; i < temp.length; i++) {
            w[i] = Integer.parseInt(temp[i]);//整数数组
        }

        String str2 = input.nextLine();
        String[] temp2 = str2.split(" ");
        int[] v = new int[temp.length];//int类型数组
        for (int i = 0; i < temp.length; i++) {
            v[i] = Integer.parseInt(temp2[i]);//整数数组
        }

        int[] w1 = new int[w.length + 1]; // 在原数组前面加个0，从而和原来的第几个物品对应起来
        System.arraycopy(w, 0, w1, 1, w.length);
        int[] v1 = new int[v.length + 1];
        System.arraycopy(v, 0, v1, 1, v.length);

        //    System.out.println(Arrays.toString(w1));
        //    System.out.println(Arrays.toString(v1));

        int res = fun(4, 8, w1, v1);
        System.out.println(res);
        
        int wNum = 5, vMax = 9;
        int[][] opt = new int[wNum][vMax];
        nfun(w1, v1, opt, wNum, vMax);
        for (int i = 0; i < opt.length; i++) {
            for (int j = 0; j < opt[0].length; j++) {
                System.out.print(opt[i][j] + "\\t");
            }
            System.out.println();
        }
    }

    /**
     * 递归的方式实现
     * @param k:当前可以偷取的第k个物品
     * @param wk：当前背包的容量
     * @return
     */
    public static int fun(int k, int wk, int[] w, int[] v) {
        if (k == 0 || wk == 0)
            return 0;
        else if (wk < w[k]) {
            return fun(k - 1, wk, w, v);
        } else {
            int A = fun(k - 1, wk, w, v);
            int B = fun(k - 1, wk - w[k], w, v) + v[k];
            return Math.max(A, B);
        }
    }

    /**
     * 非递归实现
     */
    public static void nfun(int[] w, int[] v, int[][] opt, int wNum, int vMax) {
        for (int i = 1; i < wNum; i++) {
            for (int j = 1; j < vMax; j++) {
                if (j < w[i]) { // 当前的剩余容量比物品的容量小
                    opt[i][j] = opt[i - 1][j];
                } else {
                    opt[i][j] = Math.max(opt[i - 1][j], opt[i - 1][j - w[i]] + v[i]);
                }
            }
        }
    }

}

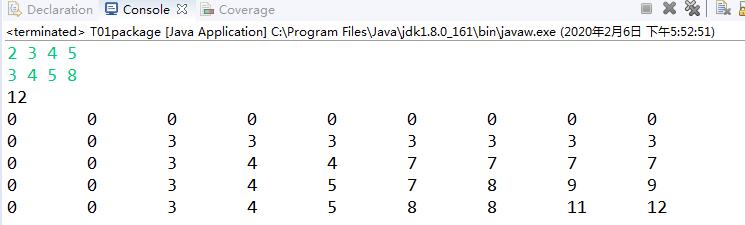
1.4最长递增子序列

给定一个长度为N的数组，找出一个最长的单调递增子序列，子序列不一定连续，但初始顺序不能乱。

例如：给定一个长度为6的数组A{4， 5， 7， 1，3， 9}，则其最长的单调递增子序列为{4，5，7，9}，长度为4。

该问题满足最优子结构性质，因此可以使用动态规划求解。

定义如下符号：

• 表示问题序列的总长度。
• 表示下标从1到i的一个序列，特别地，表示下标从1开始，长度为n的一个序列，也就是问题的输入。
• 表示中的第个元素。

由于问题的最优解必然对应某个子序列，而这个子序列又必然由某个结尾，因此，由所有结尾的最长递增序列的长度，构成了问题的解空间。因此，再引入符号L，来描述问题的解空间：

• 表示以结尾的最长递增子序列的长度。

显然，为该递增子序列的最大值，就是问题的最优解。

求解，就要得到所有的。求解这一问题，包含了求解从到的所有子问题，从而满足最优子结构性质。

递归方程如下：

转换成代码，思路就是遍历所有，选择满足的最大的，则，如果比所有都要小，则。

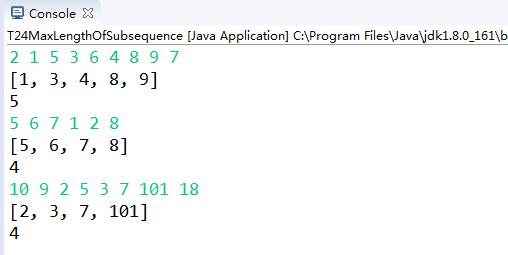
package nowcode2;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;

public class T24MaxLengthOfSubsequence {

    public static void main(String[] args) {
        Scanner input = new Scanner(System.in);
        while (input.hasNext()) {
            String str = input.nextLine();
            String[] arr = str.split(" ");
            int[] nums = new int[arr.length];
            for (int i = 0; i < nums.length; i++) {
                nums[i] = Integer.parseInt(arr[i]);
            }
            int res = getMaxLengthOfSubsequence(nums);
            System.out.println(res);
        }
        input.close();
    }

    //获得最长子序列
    public static int getMaxLengthOfSubsequence(int[] nums) {
        int n = nums.length;
        int[] ls = new int[n];
        int res = 1;

        for (int i = 0; i < n; i++) {//填充ls
            int maxValue = 1;
            ls[i] = 1;
            for (int j = 0; j < i; j++) { ///遍历所有的A
                if (nums[i] > nums[j]) {
                    maxValue = max(maxValue, ls[j] + 1);
                }
                ls[i] = maxValue;
            }
        }

        int index = 0;
        //最长子序列末尾出现的位置
        for (int i = 0; i < n; i++) { //查找最大的子序列
            if (ls[i] > res) {
                res = ls[i];
                index = i;
            }
        }
        
        int count = res; //从后往前找子序列
        int[] arrRes = new int[count];
        arrRes[--count] = nums[index];
        for (int i = index; i >= 0; i--) {
            if (nums[i] < nums[index] && ls[i] == ls[index] - 1) {
                arrRes[--count] = nums[i];
                index = i;
            }
        }
        System.out.println(Arrays.toString(arrRes));
        return res;
    }

    public static int max(int a, int b) {
        return a > b ? a : b;
    }
}