均值模型
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了均值模型相关的知识,希望对你有一定的参考价值。
原文链接:http://tecdat.cn/?p=20015
本文将说明单变量和多变量金融时间序列的不同模型,特别是条件均值和条件协方差矩阵、波动率的模型。
均值模型
本节探讨条件均值模型。
iid模型
我们从简单的iid模型开始。iid模型假定对数收益率xt为N维高斯时间序列:
均值和协方差矩阵的样本估计量分别是样本均值
和样本协方差矩阵
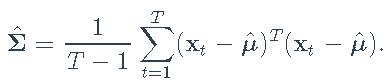
我们从生成数据开始,熟悉该过程并确保估计过程给出正确的结果(即完整性检查)。然后使用真实的市场数据并拟合不同的模型。
让我们生成合成iid数据并估算均值和协方差矩阵:
# 生成综合收益数据X <- rmvnorm(n = T, mean = mu, sigma = Sigma)# 样本估计(样本均值和样本协方差矩阵)mu_sm <- colMeans(X)Sigma_scm <- cov(X)# 误差norm(mu_sm - mu, "2")#> [1] 2.44norm(Sigma_scm - Sigma, "F")#> [1] 70.79
现在,让我们针对不同数量的观测值T再做一次:
# 首先生成所有数据X <- rmvnorm(n = T_max, mean = mu, sigma = Sigma)# 现在遍历样本的子集for (T_ in T_sweep) # 样本估算 mu_sm <- colMeans(X_) Sigma_scm <- cov(X_) # 计算误差 error_mu_vs_T <- c(error_mu_vs_T, norm(mu_sm - mu, "2")) error_Sigma_vs_T <- c(error_Sigma_vs_T, norm(Sigma_scm - Sigma, "F"))# 绘图plot(T_sweep, error_mu_vs_T, main = "mu估计误差",
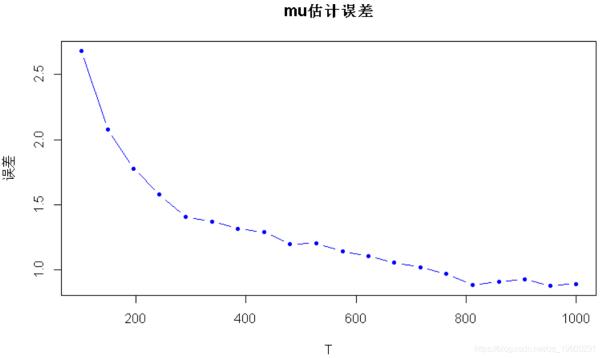
plot(T_sweep, error_Sigma_vs_T main = "Sigma估计中的误差", ylab = "误差"
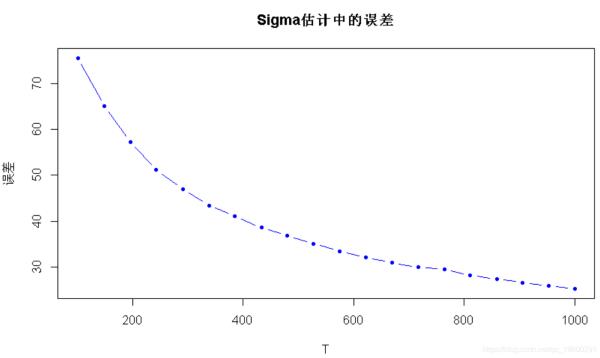
单变量ARMA模型
对数收益率xt上的ARMA(p,q)模型是
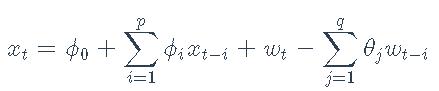
其中wt是均值为零且方差为σ2的白噪声序列。模型的参数是系数ϕi,θi和噪声方差σ2。
请注意,ARIMA(p,d,q)模型是时间差分为d阶的ARMA(p,q)模型。因此,如果我们用xt代替对数价格,那么先前的对数收益模型实际上就是ARIMA(p,1,q)模型,因为一旦对数价格差分,我们就获得对数收益。
rugarch生成数据
我们将使用rugarch包 生成单变量ARMA数据,估计参数并进行预测。
首先,我们需要定义模型:
# 指定具有给定系数和参数的AR(1)模型#> #> *----------------------------------*#> * ARFIMA Model Spec *#> *----------------------------------*#> Conditional Mean Dynamics#> ------------------------------------#> Mean Model : ARFIMA(1,0,0)#> Include Mean : TRUE #> #> Conditional Distribution#> ------------------------------------#> Distribution : norm #> Includes Skew : FALSE #> Includes Shape : FALSE #> Includes Lambda : FALSE#> Level Fixed Include Estimate LB UB#> mu 0.01 1 1 0 NA NA#> ar1 -0.90 1 1 0 NA NA#> ma 0.00 0 0 0 NA NA#> arfima 0.00 0 0 0 NA NA#> archm 0.00 0 0 0 NA NA#> mxreg 0.00 0 0 0 NA NA#> sigma 0.20 1 1 0 NA NA#> alpha 0.00 0 0 0 NA NA#> beta 0.00 0 0 0 NA NA#> gamma 0.00 0 0 0 NA NA#> eta1 0.00 0 0 0 NA NA#> eta2 0.00 0 0 0 NA NA#> delta 0.00 0 0 0 NA NA#> lambda 0.00 0 0 0 NA NA#> vxreg 0.00 0 0 0 NA NA#> skew 0.00 0 0 0 NA NA#> shape 0.00 0 0 0 NA NA#> ghlambda 0.00 0 0 0 NA NA#> xi 0.00 0 0 0 NA NAfixed.pars#> $mu#> [1] 0.01#> #> $ar1#> [1] -0.9#> #> $sigma#> [1] 0.2true_params#> mu ar1 sigma #> 0.01 -0.90 0.20
然后,我们可以生成时间序列:
# 模拟一条路径apath(spec, n.sim = T)# 转换为xts并绘图plot(synth_log_returns, main = "ARMA模型的对数收益率"plot(synth_log_prices, main = "ARMA模型的对数价格"
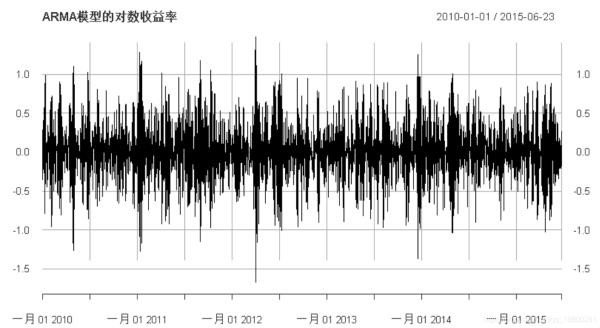
ARMA模型
现在,我们可以估计参数(我们已经知道):
# 指定AR(1)模型arfimaspec(mean.model = list(armaOrder = c(1,0), include.mean = TRUE))# 估计模型#> mu ar1 sigma #> 0.0083 -0.8887 0.1987#> mu ar1 sigma #> 0.01 -0.90 0.20
我们还可以研究样本数量T对参数估计误差的影响:
# 循环for (T_ in T_sweep) estim_coeffs_vs_T <- rbind(estim_coeffs_vs_T, coef(arma_fit)) error_coeffs_vs_T <- rbind(error_coeffs_vs_T, abs(coef(arma_fit) - true_params)/true_params)# 绘图matplot(T_sweep, estim_coeffs_vs_T, main = "估计的ARMA系数", xlab = "T", ylab = "值",
matplot(T_sweep, 100*error_coeffs_vs_T, main = "估计ARMA系数的相对误差", xlab = "T", ylab = "误差 (%)",
首先,真正的μ几乎为零,因此相对误差可能显得不稳定。在T = 800个样本之后,其他系数得到了很好的估计。
ARMA预测
为了进行健全性检查,我们现在将比较两个程序包 Forecast 和 rugarch的结果:
# 指定具有给定系数和参数的AR(1)模型spec(mean.model = list(armaOrder = c(1,0), include.mean = TRUE), fixed.pars = list(mu = 0.005, ar1 = -0.9, sigma = 0.1))# 生成长度为1000的序列arfima(arma_fixed_spec, n.sim = 1000)@path$seriesSim# 使用 rugarch包指定和拟合模型spec(mean.model = list(armaOrder = c(1,0), include.mean = TRUE))# 使用包“ forecast”拟合模型#> ARIMA(1,0,0) with non-zero mean #> #> Coefficients:#> ar1 mean#> -0.8982 0.0036#> s.e. 0.0139 0.0017#> #> sigma^2 estimated as 0.01004: log likelihood=881.6#> AIC=-1757.2 AICc=-1757.17 BIC=-1742.47# 比较模型系数#> ar1 intercept sigma #> -0.898181148 0.003574781 0.100222964#> mu ar1 sigma #> 0.003605805 -0.898750138 0.100199956
确实,这两个软件包给出了相同的结果。
ARMA模型选择
在先前的实验中,我们假设我们知道ARMA模型的阶数,即p = 1和q = 0。实际上,阶数是未知的,因此必须尝试不同的阶数组合。阶数越高,拟合越好,但这将不可避免地导致过度拟合。已经开发出许多方法来惩罚复杂性的增加以避免过度拟合,例如AIC,BIC,SIC,HQIC等。
# 尝试不同的组合# 查看排名#> AR MA Mean ARFIMA BIC converged#> 1 1 0 1 0 -0.38249098 1#> 2 1 1 1 0 -0.37883157 1#> 3 2 0 1 0 -0.37736340 1#> 4 1 2 1 0 -0.37503980 1#> 5 2 1 1 0 -0.37459177 1#> 6 3 0 1 0 -0.37164609 1#> 7 1 3 1 0 -0.37143480 1#> 8 2 2 1 0 -0.37107841 1#> 9 3 1 1 0 -0.36795491 1#> 10 2 3 1 0 -0.36732669 1#> 11 3 2 1 0 -0.36379209 1#> 12 3 3 1 0 -0.36058264 1#> 13 0 3 1 0 -0.11875575 1#> 14 0 2 1 0 0.02957266 1#> 15 0 1 1 0 0.39326050 1#> 16 0 0 1 0 1.17294875 1#选最好的armaOrder#> AR MA #> 1 0
在这种情况下,由于观察次数T = 1000足够大,因此阶数被正确地检测到。相反,如果尝试使用T = 200,则检测到的阶数为p = 1,q = 3。
ARMA预测
一旦估计了ARMA模型参数ϕi ^ i和θ^j,就可以使用该模型预测未来的值。例如,根据过去的信息对xt的预测是
并且预测误差将为xt-x ^ t = wt(假设参数已被估计),其方差为σ2。软件包 rugarch 使对样本外数据的预测变得简单:
# 估计模型(不包括样本外)coef(arma_fit)#> mu ar1 sigma #> 0.007212069 -0.898745183 0.200400119# 整个样本外的预测对数收益forecast_log_returns <- xts(arma_fore@forecast$seriesFor[1, ], dates_out_of_sample)# 恢复对数价格prev_log_price <- head(tail(synth_log_prices, out_of_sample+1), out_of_sample)# 对数收益图plot(cbind("fitted" = fitted(arma_fit),# 对数价格图plot(cbind("forecast" = forecast_log_prices, main = "对数价格预测", legend.loc = "topleft")
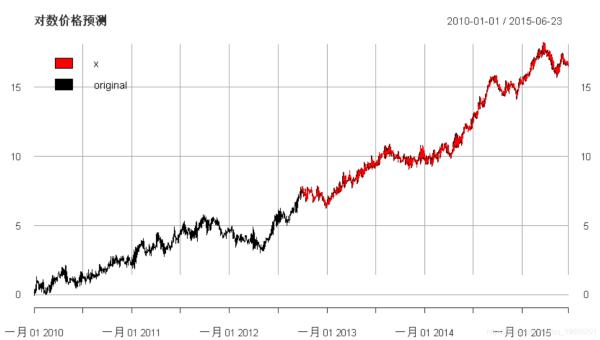
多元VARMA模型
对数收益率xt上的VARMA(p,q)模型是
其中wt是具有零均值和协方差矩阵Σw的白噪声序列。该模型的参数是矢量/矩阵系数ϕ0,Φi,Θj和噪声协方差矩阵Σw。
比较
让我们首先加载S&P500:
# 加载标普500数据head(SP500_index_prices)#> SP500#> 2012-01-03 1277.06#> 2012-01-04 1277.30#> 2012-01-05 1281.06#> 2012-01-06 1277.81#> 2012-01-09 1280.70#> 2012-01-10 1292.08# 准备训练和测试数据logreturns_trn <- logreturns[1:T_trn]logreturns_tst <- logreturns[-c(1:T_trn)]# 绘图 plot(logreturns, addEventLines(xts("训练"
现在,我们使用训练数据(即,对于t = 1,…,Ttrnt = 1,…,Ttrn)来拟合不同的模型(请注意,通过指示排除了样本外数据 out.sample = T_tst)。特别是,我们将考虑iid模型,AR模型,ARMA模型以及一些ARCH和GARCH模型(稍后将对方差建模进行更详细的研究)。
# 拟合i.i.d.模型coef(iid_fit)#> mu sigma #> 0.0005712982 0.0073516993mean(logreturns_trn)#> [1] 0.0005681388sd(logreturns_trn)#> [1] 0.007360208# 拟合AR(1)模型coef(ar_fit)#> mu ar1 sigma #> 0.0005678014 -0.0220185181 0.0073532716# 拟合ARMA(2,2)模型coef(arma_fit)#> mu ar1 ar2 ma1 ma2 sigma #> 0.0007223304 0.0268612636 0.9095552008 -0.0832923604 -0.9328475211 0.0072573570# 拟合ARMA(1,1)+ ARCH(1)模型coef(arch_fit)#> mu ar1 ma1 omega alpha1 #> 6.321441e-04 8.720929e-02 -9.391019e-02 4.898885e-05 9.986975e-02#拟合ARMA(0,0)+ARCH(10)模型coef(long_arch_fit)#> mu omega alpha1 alpha2 alpha3 alpha4 alpha5 #> 7.490786e-04 2.452099e-05 6.888561e-02 7.207551e-02 1.419938e-01 1.909541e-02 3.082806e-02 #> alpha6 alpha7 alpha8 alpha9 alpha10 #> 4.026539e-02 3.050040e-07 9.260183e-02 1.150128e-01 1.068426e-06# 拟合ARMA(1,1)+GARCH(1,1)模型coef(garch_fit)#> mu ar1 ma1 omega alpha1 beta1 #> 6.660346e-04 9.664597e-01 -1.000000e+00 7.066506e-06 1.257786e-01 7.470725e-01
当数学规划问题中出现随机变量时,处理这些随机变量的一个很自然的方法是利用这些随机变量的概率平均值(数学期望)来替代随机变量本身,从而形成一个确定性的数学规划问题,这种方法简单实用,但并不是在所有条件下都合适,在很多情况下,利用随机变量均值所做的决策往往会破坏约束条件。下列规划模型就是一例:
例:设(a,b)是矩形1≤a≤4,1/3≤b≤1内均匀分布的随机向量,求解下列线性规划问题:
地下水系统随机模拟与管理
容易求出 a,b 的数学期望值分别为,如用 E(a),E(b)分别代替原规划模型中的 a,b,则形成下列确定性线性规划问题:
地下水系统随机模拟与管理
利用单纯形法容易得知上述线性规划问题有最优解:
地下水系统随机模拟与管理
若设
地下水系统随机模拟与管理
则有:
地下水系统随机模拟与管理
它说明该规划问题的最优解x*位于可行域D的概率仅为0.25。显然这一随机规划问题的最优解失去了它的使用意义。于是,就出现了新的处理规划问题中随机变量的方法,其中最常见的一种方法就是等待观察到随机变量的实现以后,解出相应的规划问题。另一种则是在观察到随机变量的实现之前便做出决策,但应事先要求做出的决策是不可能解的概率不超过某一个给定的数。
- 官方服务
- 官方网站
模型思维2-中心极限定理的应用
1、什么是中心极限定理
[]用样本来估计总体(任何一个样本的平均值,将会约等于其所在总体的平均值)
[]样本的平均值成正态分布
2、应用条件
[]事件相互独立
[]事件之间的值是有限的
3、样本来估计总体
用样本来估计总体。任何一个样本的平均值将会约等于其所在总体的平均值。
一个正确抽取的家庭样本应该能够反映中国所有家庭的情况,里面会包含收入高的公司高管,也会包括普通的员工,快递小哥、警察以及其他人,这些人出现的频率与他们在人口构成中的占比相关。因此,我们能够推测,这个包含1000个中国家庭代表性样本的家庭财富的平均值约等于总体的平均值。
4、样本平均值成正态分布
如果我们连续抽取100次包含1000个家庭的样本,并将它们的平均值的出现频率在坐标轴上标出,那么我们基本可以确定在总体平均值周围将会呈现正态分布。
取样次数越多,结果就越接近正态分布;而且样本大小越大,分布就越接近正态分布。
5、样本来估计总体标准差
现在我们已经可以用样本来估计出总体平均值。现在我想用样本来估计出总体的标准差,该怎么办呢?
我们已经知道,一个数据集的标准差是数值与平均值的偏离程度。
当你选择一个样本后,相比总体,你拥有数据的数量是变少了,因此,与总体中的数值偏离平均值的程度相比,样本中很有可能把较为极端的数值排除在外,这样使得数值更有可能以更紧密的方式聚集在均值周围。也就是说,样本的标准差要小于总体标准差。所以,为了更好的用样本估计总体的标准差,统计学家就将标准差的公式做了像下面图中公式中这样的改造。

即原来的标准差公式是除以n,为了用样本估计总体标准差,现在是除以n-1。这样就是的标准略大。一般用字幕s表示用样本估计出的总体标准差。
很多书上都会把除以n-1的标准差叫做样本标准,其实会给很多人造成误解。其实这个样本标准差的目的是用于估计总体标准差。
你可能会疑惑,那我什么时候标准差除以n还是n-1呢?
那就要看你使用标准差的目的是什么。
如果你只是想计算一个数据集的标准差,那么就除以n,例如你有100个毕业与清华人的收入,只是想了解这100个人构成的数据集的波动大小,那你就用除以n的标准差公式。
如果你想把这100个人当成一个样本,用这个样本来估计出总体(所有毕业与清华人的收入)的标准差,那么就除以n-1的标准差公式。
举个例子:
如果我从毕业于清华大学中抽取100个人作为样本1,然后我计算出标准差。那么这个标准差就是用来描述这100个人组成的数据集的波动大小。
我连续刚才重复抽取样本的动作,最后抽取出2个样本,每个样本都有100个人。对每个样本计算平均值,这样就有2个平均值。
这2个平均值其实组成了1个新的数据集,就是所有的“样本平均值”。然后对这2个平均值数据计算出标准差。就是标准误差。
6、样本平均值概率图
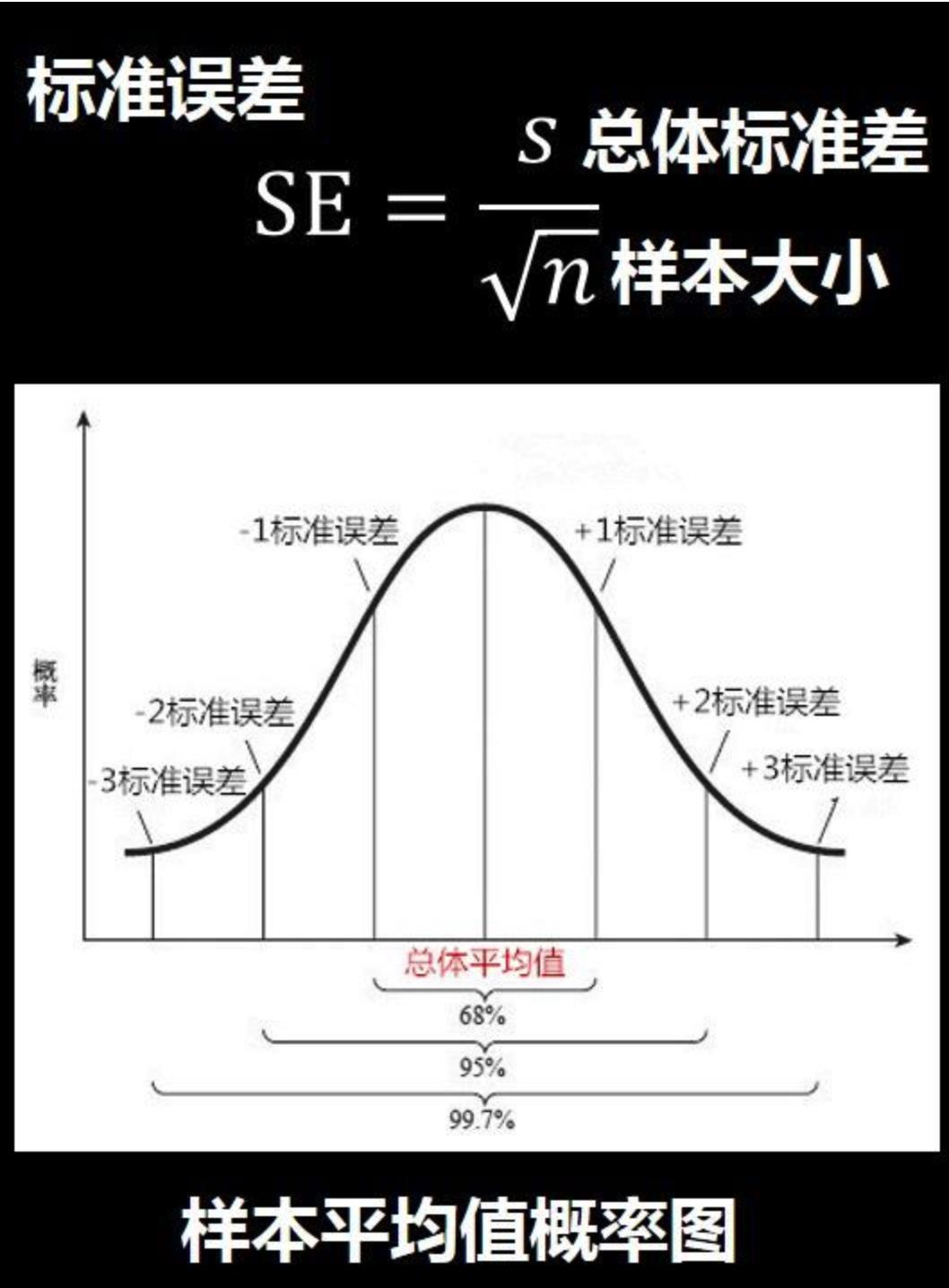
上图的含义是:
1)有68%的样本平均值会在总体平均值一个标准误差的范围之内
数值范围(总体平均值-1个标准误差,总体平均值+1个标准误差)
2)有95%的样本平均值会在总体平均值的两个标准误差的范围之内
(总体平均值-2个标准误差,总体平均值+2个标准误差)
3)有99.7%的样本平均值会在总体平均值3个标准误差的范围之内。
(总体平均值-3个标准误差,总体平均值+3个标准误差)
6、售出多少个飞机票合适呢?
例如我们飞机票的座位数目是380个,每个人来机场的概率是90%,那么我们卖出多少个座位合适呢? 比如我们卖出400个座位,由于该场景是二项分布,所以我们可以得出
平均值=360 标准差=6
那么根据上面的概率分布图,我们可以得出以下结果:
68%的概率,人数会在[354,366]之间
95%的概率,人数会在[342,372]之间
99.7%的概率,人数会在[342,378]之间
7、反推某个样本适合符合总体趋势
假如某个样本的平均值减去总体的平均值,大于3个标准误差。根据99.7%的样本平均值会处于总体平均值3个标准误差的范围内,因此我们可以得出该样本不属于总体。
文章参考自:https://www.zhihu.com/question/22913867/answer/250046834
以上是关于均值模型的主要内容,如果未能解决你的问题,请参考以下文章