matlab怎样进行频谱分析
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了matlab怎样进行频谱分析相关的知识,希望对你有一定的参考价值。
参考技术A 姓名:张猛【嵌牛导读】:如何对一个信号画出频谱并进行分析,从频谱中得到有用的信息
引用:http://blog.sina.com.cn/s/blog_a07f4fe301013gj3.html
【嵌牛鼻子】:matlab fft 频域
【嵌牛提问】:如何画频谱,对频谱如何分析
【嵌牛正文】
图像的频率是表征图像中灰度变化剧烈程度的指标,是灰度在平面空间上的梯度。如:大面积的沙漠在图像中是一片灰度变化缓慢的区域,对应的频率值很低;而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域,对应的频率值较高。傅立叶变换在实际中有非常明显的物理意义,设f是一个能量有限的模拟信号,则其傅立叶变换就表示f的谱。从纯粹的数学意义上看,傅立叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看,傅立叶变换是将图像从空间域转换到频率域,其逆变换是将图像从频率域转换到空间域。换句话说,傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数,傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数。
这样通过观察傅立叶变换后的频谱图,也叫功率图,我们首先就可以看出,图像的能量分布,如果频谱图中暗的点数更多,那么实际图像是比较柔和的(因为各点与邻域差异都不大,梯度相对较小),反之,如果频谱图中亮的点数多,那么实际图像一定是尖锐的,边界分明且边界两边像素差异较大的。对频谱移频到原点以后,可以看出图像的频率分布是以原点为圆心,对称分布的。将频谱移频到圆心除了可以清晰地看出图像频率分布以外,还有一个好处,它可以分离出有周期性规律的干扰信号,比如正弦干扰,一副带有正弦干扰,移频到原点的频谱图上可以看出除了中心以外还存在以某一点为中心,对称分布的亮点集合,这个集合就是干扰噪音产生的,这时可以很直观的通过在该位置放置带阻滤波器消除干扰。另外我还想说明以下几点:
1、图像经过二维傅立叶变换后,其变换系数矩阵表明:
若变换矩阵Fn原点设在中心,其频谱能量集中分布在变换系数短阵的中心附近(图中阴影区)。若所用的二维傅立叶变换矩阵Fn的原点设在左上角,那么图像信号能量将集中在系数矩阵的四个角上。这是由二维傅立叶变换本身性质决定的。同时也表明一股图像能量集中低频区域。
2 、变换之后的图像在原点平移之前四角是低频,最亮,平移之后中间部分是低频,最亮,亮度大说明低频的能量大(幅角比较大)。
从计算机处理精度上就不难理解,一个长度为N的信号,最多只能有N/2+1个不同频率,再多的频率就超过了计算机所能所处理的精度范围)
X[]数组又分两种,一种是表示余弦波的不同频率幅度值:Re X[],另一种是表示正弦波的不同频率幅度值:Im X[],Re是实数(Real)的意思,Im是虚数(Imagine)的意思,采用复数的表示方法把正余弦波组合起来进行表示,但这里我们不考虑复数的其它作用,只记住是一种组合方法而已,目的是为了便于表达(在后面我们会知道,复数形式的傅立叶变换长度是N,而不是N/2+1)。
用Matlab实现快速傅立叶变换
FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
虽然很多人都知道FFT是什么,可以用来做什么,怎么去做,但是却不知道FFT之后的结果是什意思、如何决定要使用多少点来做FFT。
现在就根据实际经验来说说FFT结果的具体物理意义。一个模拟信号,经过ADC采样之后,就变成了数字信号。采样定理告诉我们,采样频率要大于信号频率的两倍,这些我就不在此啰嗦了。
采样得到的数字信号,就可以做FFT变换了。N个采样点,经过FFT之后,就可以得到N个点的FFT结果。为了方便进行FFT运算,通常N取2的整数次方。
假设采样频率为Fs,信号频率F,采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。而第一个点就是直流分量,它的模值就是直流分量的N倍。而每个点的相位呢,就是在该频率下的信号的相位。第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs,这中间被N-1个点平均分成N等份,每个点的频率依次增加。例如某点n所表示的频率为:Fn=(n-1)*Fs/N。由上面的公式可以看出,Fn所能分辨到频率为Fs/N,如果采样频率Fs为1024Hz,采样点数为1024点,则可以分辨到1Hz。1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到0.5Hz。如果要提高频率分辨力,则必须增加采样点数,也即采样时间。频率分辨率和采样时间是倒数关系。
假设FFT之后某点n用复数a+bi表示,那么这个复数的模就是An=根号a*a+b*b,相位就是Pn=atan2(b,a)。根据以上的结果,就可以计算出n点(n≠1,且n<=N/2)对应的信号的表达式为:An/(N/2)*cos(2*pi*Fn*t+Pn),即2*An/N*cos(2*pi*Fn*t+Pn)。对于n=1点的信号,是直流分量,幅度即为A1/N。由于FFT结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一半的结果。
下面以一个实际的信号来做说明。假设我们有一个信号,它含有2V的直流分量,频率为50Hz、相位为-30度、幅度为3V的交流信号,以及一个频率(f0)为75Hz、相位为90度、幅度为1.5V的交流信号。用数学表达式就是如下:S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)。式中cos参数为弧度,所以-30度和90度要分别换算成弧度。我们以256Hz的采样率对这个信号进行采样,总共采样256点。按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是1Hz,第n个点的频率就是n-1。我们的信号有3个频率:0Hz、50Hz、75Hz,应该分别在第1个点、第51个点、第76个点上出现峰值,其它各点应该接近0。实际情况如何呢?我们来看看FFT的结果的模值如图所示。
从图中我们可以看到,在第1点、第51点、和第76点附近有比较大的值。我们分别将这三个点附近的数据拿上来细看:1点:512+0i2点:-2.6195E-14 - 1.4162E-13i3点:-2.8586E-14 - 1.1898E-13i50点:-6.2076E-13 - 2.1713E-12i51点:332.55 - 192i52点:-1.6707E-12 - 1.5241E-12i75点:-2.2199E-13 -1.0076E-12i76点:3.4315E-12 + 192i77点:-3.0263E-14 +7.5609E-13i很明显,1点、51点、76点的值都比较大,它附近的点值都很小,可以认为是0,即在那些频率点上的信号幅度为0。接着,我们来计算各点的幅度值。分别计算这三个点的模值,结果如下:1点:51251点:38476点:192按照公式,可以计算出直流分量为:512/N=512/256=2;50Hz信号的幅度为:384/(N/2)=384/(256/2)=3;75Hz信号的幅度为192/(N/2)=192/(256/2)=1.5。可见,从频谱分析出来的幅度是正确的。然后再来计算相位信息。直流信号没有相位可言,不用管它。先计算50Hz信号的相位,atan2(-192, 332.55)=-0.5236,结果是弧度,换算为角度就是180*(-0.5236)/pi=-30.0001。再计算75Hz信号的相位,atan2(192, 3.4315E-12)=1.5708弧度,换算成角度就是180*1.5708/pi=90.0002。可见,相位也是对的。根据FFT结果以及上面的分析计算,我们就可以写出信号的表达式了,它就是我们开始提供的信号。
总结:假设采样频率为Fs,采样点数为N,做FFT之后,某一点n(n从1开始)表示的频率为:Fn=(n-1)*Fs/N;该点的模值除以N/2就是对应该频率下的信号的幅度(对于直流信号是除以N);该点的相位即是对应该频率下的信号的相位。相位的计算可用函数atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值,范围从-pi到pi。要精确到xHz,则需要采样长度为1/x秒的信号,并做FFT。要提高频率分辨率,就需要增加采样点数,这在一些实际的应用中是不现实的,需要在较短的时间内完成分析。解决这个问题的方法有频率细分法,比较简单的方法是采样比较短时间的信号,然后在后面补充一定数量的0,使其长度达到需要的点数,再做FFT,这在一定程度上能够提高频率分辨力。具体的频率细分法可参考相关文献。
附贴上上述例子的matlab程序:
Matlab的例子(一)
t=0:1/256:1;%采样步长
y= 2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180);
N=length(t); %样点个数
plot(t,y);
fs=256;%采样频率
df=fs/(N-1);%分辨率
f=(0:N-1)*df;%其中每点的频率
Y=fft(y)/N*2;%真实的幅值
%Y=fftshift(Y);
figure(2)
plot(f,abs(Y));
由于以上程序是结合傅里叶算法转换得到的对称图,而常用的只需要一半就可以了。对应的程序如下:
t=0:1/256:1;%采样步长
y= 2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180);
N=length(t); %样点个数
plot(t,y);
fs=256;%采样频率
df=fs/(N-1);%分辨率
f=(0:N-1)*df;%其中每点的频率
Y=fft(y(1:N))/N*2;%真实的幅值
%Y=fftshift(Y);
figure(2)
plot(f(1:N/2),abs(Y(1:N/2)));
频域分析频谱泄露频率分辨率栅栏效应
信号的频域分析
一、时域加窗
现实生活中的信号大部分是连续的,通过对连续的信号进行采样得到散时间信号,但是计算机所能处理的数据都是有限长的,因而我们可以对原始序列做加窗处理使其成为有限长序列。
以矩形窗为例,其时域表达式为:
式(1)中,
N
=
M
+
1
N=M+1
N=M+1,为矩形窗的长度。
对无限长序列进行加窗处理,就是对序列在时域上乘以一个窗函数。
由卷积定理可以得到,时域的相乘等于频域的卷积。
设仿真信号的时域表达式为:
x
(
t
)
=
A
0
∗
c
o
s
(
2
π
f
0
t
)
+
A
1
∗
c
o
s
(
2
π
f
1
t
)
x(t)=A_{0}*cos(2πf_{0}t)+A_{1}*cos(2πf_{1}t)
x(t)=A0∗cos(2πf0t)+A1∗cos(2πf1t)
x
(
t
)
x(t)
x(t)做傅里叶变换(FT)的频域表达式为:
X
(
j
Ω
)
=
A
0
π
δ
(
Ω
+
Ω
0
)
+
A
0
π
δ
(
Ω
−
Ω
0
)
+
A
1
π
δ
(
Ω
+
Ω
0
)
+
A
1
π
δ
(
Ω
−
Ω
0
)
X(jΩ)=A_{0}πδ(Ω+Ω_{0})+A_{0}πδ(Ω-Ω_{0})+A_{1}πδ(Ω+Ω_{0})+A_{1}πδ(Ω-Ω_{0})
X(jΩ)=A0πδ(Ω+Ω0)+A0πδ(Ω−Ω0)+A1πδ(Ω+Ω0)+A1πδ(Ω−Ω0)
连续信号
x
(
t
)
x(t)
x(t)的波形及频谱如图1所示。

连续信号
x
(
t
)
x(t)
x(t)经过采样后,得到的离散时间的表达式为:
x
[
n
]
=
x
(
t
)
∣
t
=
n
T
s
x[n]=x(t)|_{t=nT_{s}}
x[n]=x(t)∣t=nTs
离散序列
x
[
n
]
x[n]
x[n]做离散时间傅里叶变换(DTFT)的频域表达式为:
X
(
e
j
w
)
=
1
T
s
∑
k
=
−
∞
∞
X
(
j
w
T
s
−
j
k
2
π
T
s
)
X(e^{jw})=\\frac{1}{T_{s}}\\sum_{k=-∞}^{∞}X(j\\frac{w}{T_{s}}-jk\\frac{2π}{T_{s}})
X(ejw)=Ts1k=−∞∑∞X(jTsw−jkTs2π)
离散序列
x
[
n
]
x[n]
x[n]的波形及频谱如图2所示。

矩形窗函数
w
[
n
]
w[n]
w[n]做离散时间傅里叶变换(DTFT)的频域表达式为:
W
(
e
j
w
)
=
e
−
j
w
(
N
−
1
)
/
2
∗
s
i
n
(
w
N
/
2
)
s
i
n
(
w
/
2
)
W(e^{jw})=e^{-jw(N-1)/2} *\\frac{sin(wN/2)}{sin(w/2)}
W(ejw)=e−jw(N−1)/2∗sin(w/2)sin(wN/2)
矩形窗函数
w
[
n
]
w[n]
w[n]的波形及频谱如图3所示。

离散序列
x
[
n
]
x[n]
x[n]与窗函数
w
[
n
]
w[n]
w[n]的卷积为:
V
(
e
j
w
)
=
1
2
π
∫
−
π
π
X
(
e
j
θ
)
W
(
e
j
(
w
−
θ
)
)
d
θ
=
A
0
2
W
(
e
j
(
w
+
w
0
)
)
+
A
0
2
W
(
e
j
(
w
−
w
0
)
)
+
A
1
2
W
(
e
j
(
w
+
w
0
)
)
+
A
1
2
W
(
e
j
(
w
−
w
0
)
)
V(e^{jw})=\\frac{1}{2π}\\int_{-π}^{π}X(e^{jθ})W(e^{j(w-θ)})dθ=\\frac{A_{0}}{2}W(e^{j(w+w_{0})})+\\frac{A_{0}}{2}W(e^{j(w-w_{0})})+\\frac{A_{1}}{2}W(e^{j(w+w_{0})})+\\frac{A_{1}}{2}W(e^{j(w-w_{0})})
V(ejw)=2π1∫−ππX(ejθ)W(ej(w−θ))dθ=2A0W(ej(w+w0))+2A0W(ej(w−w0))+2A1W(ej(w+w0))+2A1W(ej(w−w0))
截断后的离散序列
v
[
n
]
v[n]
v[n]的波形及频谱如图4所示。

频谱泄露
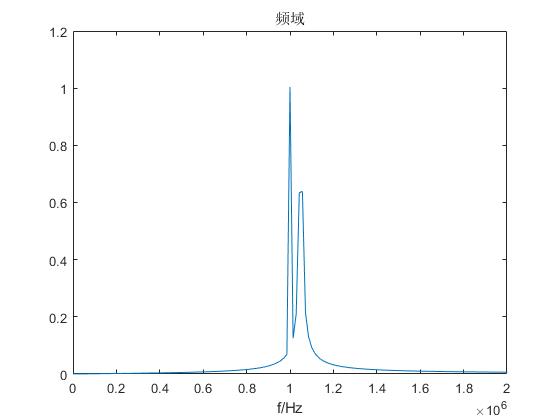
信号的频率成分包括1MHz和1.05MHz,1MHz对应的幅值为1,但是1.05MHz的幅值减小了,且在其他频率点上都有不小的幅值。这就是出现了频谱泄露的现象。
产生频谱泄露的原因是什么?
由于计算机只能处理有限长的数据,所以需要对采集的信号进行截断,相当于对原始信号做了加窗处理。对信号加窗就是对信号在时域上乘以一个窗函数,时域的乘积对应频域的卷积,而窗函数的频域包括主瓣和旁瓣,旁瓣造成了信号频谱的泄漏。频域泄漏不可避免,只能减小。
如何抑制这一现象?
可以取更长的数据点
以上是关于matlab怎样进行频谱分析的主要内容,如果未能解决你的问题,请参考以下文章