结对编程(Java实现)
Posted Lyongjie
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了结对编程(Java实现)相关的知识,希望对你有一定的参考价值。
- GitHub地址
https://github.com/Importlif/ARi
- PSP表格
|
PSP2.1 |
Personal Software Process Stages |
预估耗时(分钟) |
实际耗时(分钟) |
|
Planning |
计划 |
60 |
80 |
|
· Estimate |
· 估计这个任务需要多少时间 |
60 |
80 |
|
Development |
开发 |
2880 |
3100 |
|
· Analysis |
· 需求分析 (包括学习新技术) |
240 |
200 |
|
· Design Spec |
· 生成设计文档 |
120 |
100 |
|
· Design Review |
· 设计复审 (和同事审核设计文档) |
60 |
100 |
|
· Coding Standard |
· 代码规范 (为目前的开发制定合适的规范) |
120 |
150 |
|
· Design |
· 具体设计 |
240 |
300 |
|
· Coding |
· 具体编码 |
1800 |
2000 |
|
· Code Review |
· 代码复审 |
120 |
100 |
|
· Test |
· 测试(自我测试,修改代码,提交修改) |
180 |
150 |
|
Reporting |
报告 |
300 |
280 |
|
· Test Report |
· 测试报告 |
120 |
100 |
|
· Size Measurement |
· 计算工作量 |
60 |
80 |
|
· Postmortem & Process Improvement Plan |
· 事后总结, 并提出过程改进计划 |
120 |
100 |
|
合计 |
|
3240 |
3460 |
- 效能分析
- 在讨论如何生成题目的过程中,我们两人有不同的想法,一种是利用字符串类型String去生成并存储生成的题目,另一种想法是通过结合两个数组分别去存储运算数和运算符号,在经过性能分析、运算量分析、实现的复杂度等过程后,我们认为采用第一种方法的效率可能会更高。
- 同时在做完项目后,通过查阅网上资料,发现在四则运算中可以采用后缀表达式的方法,对比我们的计算方法,后缀表达式的算法在速度上应该是更胜一筹的,但是要占用额外的栈开销,各有各的优点。而且我们的计算方法,可以模拟人的计算过程,给出一步一步的计算过程,有助于使用者分析中间结果
- 在查重的算法方面,我们的想法是遇到相同结果的题目再拿出来判断是否能通过变换获得,但是后来我们觉得,在混合了整数、分数、真分数的四则运算中,出现重复的概率是极小的只要当给定的范围够大(在10左右就基本不可能重复了),因此我们决定,当出现结果重复时直接重新生成一道题目,减少计算量。
- 程序结构
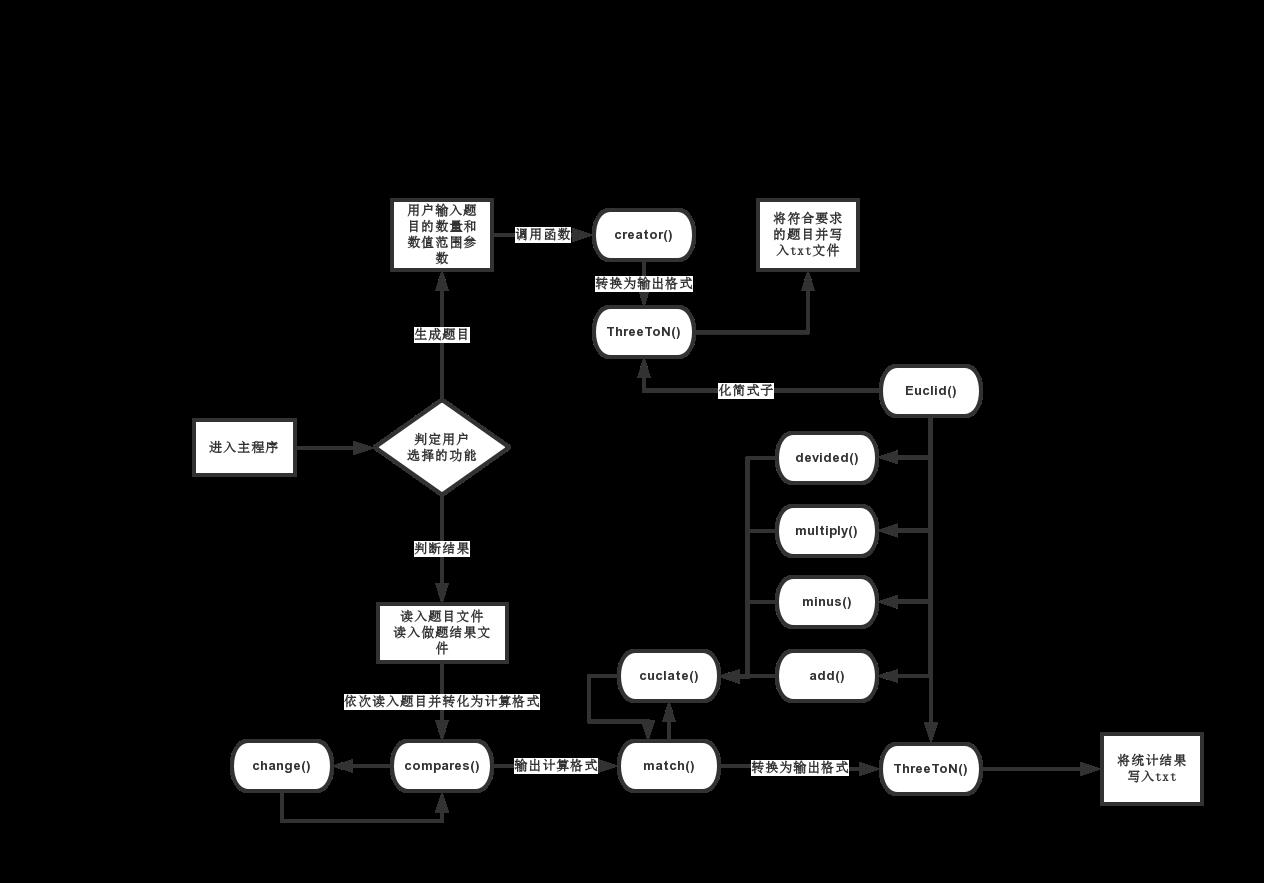
- 关键代码说明
计算结果函数
String cuclate(String str) { while(str.indexOf("÷")!=-1||str.indexOf("×")!=-1) { int pos; for(pos=0;;pos++) { if(str.charAt(pos)==\'×\'||str.charAt(pos)==\'÷\') { break; } } int mark; String leftStr=""; mark = pos - 1; while (mark >= 0 && (str.charAt(mark) != \'+\' && str.charAt(mark) != \'-\' && str.charAt(mark) != \'×\' && str.charAt(mark) != \'÷\')) { mark--; } if (mark > 0) { leftStr = str.substring(0,mark+1); } mark++; String sub=str.substring(mark, pos); long i=Long.parseLong(sub.substring(0,sub.indexOf("’"))); long i1=Long.parseLong(sub.substring(sub.indexOf("’")+1,sub.indexOf("/"))); long i2=Long.parseLong(sub.substring(sub.indexOf("/")+1)); String rightStr=""; mark = pos + 1; while (mark < str.length() && (str.charAt(mark) != \'+\' && str.charAt(mark) != \'-\' && str.charAt(mark) != \'×\' && str.charAt(mark) != \'÷\')) { mark++; } mark--; if (mark < str.length()-1) { rightStr = str.substring(mark+1); } String sub1=str.substring(pos+1, mark+1); long j=Long.parseLong(sub1.substring(0,sub1.indexOf("’"))); long j1=Long.parseLong(sub1.substring(sub1.indexOf("’")+1,sub1.indexOf("/"))); long j2=Long.parseLong(sub1.substring(sub1.indexOf("/")+1)); if (str.charAt(pos)==\'×\') { long result[]=multiply(new long[] {i,i1,i2},new long[] {j,j1,j2}); str=leftStr+Long.toString(result[0])+"’"+Long.toString(result[1])+"/"+Long.toString(result[2])+rightStr; } else { long result[]=devided(new long[] {i,i1,i2},new long[] {j,j1,j2}); str=leftStr+Long.toString(result[0])+"’"+Long.toString(result[1])+"/"+Long.toString(result[2])+rightStr; } } while(str.indexOf("+")!=-1||str.indexOf("-")!=-1) { int pos; for(pos=0;;pos++) { if(str.charAt(pos)==\'+\'||str.charAt(pos)==\'-\') { break; } } int mark; String leftStr=""; mark = pos - 1; while (mark >= 0 && (str.charAt(mark) != \'+\' && str.charAt(mark) != \'-\' && str.charAt(mark) != \'×\' && str.charAt(mark) != \'÷\')) { mark--; } if (mark > 0) { leftStr = str.substring(0,mark+1); } mark++; String sub=str.substring(mark, pos); long i=Long.parseLong(sub.substring(0,sub.indexOf("’"))); long i1=Long.parseLong(sub.substring(sub.indexOf("’")+1,sub.indexOf("/"))); long i2=Long.parseLong(sub.substring(sub.indexOf("/")+1)); String rightStr=""; mark = pos + 1; while (mark <str.length() && (str.charAt(mark) != \'+\' && str.charAt(mark) != \'-\' && str.charAt(mark) != \'×\' && str.charAt(mark) != \'÷\')) { mark++; } mark--; if (mark < str.length()-1) { rightStr = str.substring(mark+1); } String sub1=str.substring(pos+1, mark+1); long j=Long.parseLong(sub1.substring(0,sub1.indexOf("’"))); long j1=Long.parseLong(sub1.substring(sub1.indexOf("’")+1,sub1.indexOf("/"))); long j2=Long.parseLong(sub1.substring(sub1.indexOf("/")+1)); if (str.charAt(pos)==\'+\') { long result[]=add(new long[] {i,i1,i2},new long[] {j,j1,j2}); str=leftStr+Long.toString(result[0])+"’"+Long.toString(result[1])+"/"+Long.toString(result[2])+rightStr; } else { long result[]=minus(new long[] {i,i1,i2},new long[] {j,j1,j2}); if(result[0]<0||result[1]<0) { return "false"; } str=leftStr+Long.toString(result[0])+"’"+Long.toString(result[1])+"/"+Long.toString(result[2])+rightStr; } } return str; } public String match(String str)// { Stack<Integer> stack=new Stack<Integer>(); for(int i=0;i<str.length();i++) { if(str.charAt(i)==\'(\') { stack.push(i); } if(str.charAt(i)==\')\') { int tag=(int) stack.peek(); stack.pop(); String check; check=cuclate(str.substring(tag+1, i)); if(check.equals("false")) { return "false"; } str=str.substring(0,tag)+cuclate(str.substring(tag+1,i))+str.substring(i+1);//先算括号里面的,从而去掉括号 i=0; } } if(str.length()>0 &&str.indexOf("(")==-1){ str=cuclate(str);//没括号的话直接算 } else str = match(str); return str; }
在match函数中,通过使用栈的方法进行括号匹配,实现有括号先算括号,把遇到的左括号的位置压入栈中,当遇到右括号时,取出栈顶元素,将左右括号之间的式子调用cuclate函数进行计算并返回结果。在cuclate函数中,按照四则运算法则进行计算,先乘除,后加减,计算完成后返回结果。同时在cuclate中遇到减法时检测计算结果,如果出现负数则返回false,并舍弃该题目重新生成。
题目生成函数
public String creator(long r) { //随机决定生成带分数或分数或整数 int decide = (int)(Math.random() * 3) + 1; String str ; switch(decide){//真分数二又八分之三表示为2’3/8。 case 1 : long sumc = (long)(Math.random() * r-1) + 1; long fenmuc = (long)(Math.random() * r-1) + 2; long fenzic = (long)(Math.random() * fenmuc-1) + 1; while(Euclid(fenmuc,fenzic) != 1) {//生成不可约的分数 fenmuc = (long)(Math.random() * r-1) + 2; fenzic = (long)(Math.random() * fenmuc-1) + 1; } str = String.valueOf(sumc)+"’"+String.valueOf(fenzic)+"/"+String.valueOf(fenmuc);break; case 2 : long fenmud = (long)(Math.random() * r-1) + 2; long fenzid = (long)(Math.random() * fenmud-1) + 1; while(Euclid(fenmud,fenzid) != 1) {//生成不可约的分数 fenmud = (long)(Math.random() * r-1) + 2; fenzid = (long)(Math.random() * fenmud-1) + 1; } str = String.valueOf(fenzid)+"/"+String.valueOf(fenmud);break; default: long sum = (long)(Math.random() * r-1) + 1; str = String.valueOf(sum);break; }//生成第一个数str int sign_num = (int)(Math.random() * 3) + 1;//随机决定总共生成多少个数 while(sign_num != 0) { //生成后面的式子 int decide2 = (int)(Math.random() * 3) + 1;//随机决定生成带分数或分数或整数 String str2 ; switch(decide2){//真分数二又八分之三表示为2’3/8。 case 1 : long sumc2 = (long)(Math.random() * r-1) + 1; long fenmuc2 = (long)(Math.random() * r-1) + 2; long fenzic2 = (long)(Math.random() * fenmuc2-1) + 1; while(Euclid(fenmuc2,fenzic2) != 1) {//生成不可约的分数 fenmuc2 = (long)(Math.random() * r-1) + 2; fenzic2 = (long)(Math.random() * fenmuc2-1) + 1; } str2 = String.valueOf(sumc2)+"’"+String.valueOf(fenzic2)+"/"+String.valueOf(fenmuc2);break; case 2 : long fenmu2 = (long)(Math.random() * r-1) + 2; long fenzi2 = (long)(Math.random() * fenmu2-1) + 1; while(Euclid(fenmu2,fenzi2) != 1) {//生成不可约的分数 fenmu2 = (long)(Math.random() * r-1) + 2; fenzi2 = (long)(Math.random() * fenmu2-1) + 1; } str2 = String.valueOf(fenzi2)+"/"+String.valueOf(fenmu2);break; default: long sum2 = (long)(Math.random() * r-1) + 1; str2 = String.valueOf(sum2);break; } int sign_flag = (int)(Math.random() * 4) + 1; switch(sign_flag){//真分数二又八分之三表示为2’3/8。 case 1 : str = str +"+"+str2;break; case 2 : str = str +"-"+str2;break; case 3 : str = str +"×"+str2;break; default : str = str +"÷"+str2; int bracket = (int)(Math.random() * 2) + 1; if(bracket == 1 && sign_num != 1 && ( str.indexOf("-")!= -1 ||str.indexOf("+")!= -1)) str = "("+str+")"; } sign_num--; } return str; }
生成题目思路:
1.先随机生成一个数:用random()方法,随机决定生成一个数(1或2或3),如果是1,则生成一个带分数,如果是2,则生成一个分数;如果是3,则生成一个整数。作为一个字符串。假如生成“5/8”。
2.再随机生成一个数:用random()方法,随机决定生成一个数(1或2或3),如果是1,则生成一个带分数,如果是2,则生成一个分数;如果是3,则生成一个整数。作为一个字符串。假如生成“9”。
3.再随机生成一个符号将上述两个数拼接起来成为一条式子:用random()方法,随机决定生成一个数(1或2或3或4),如果是1,则生成+,如果是2,则生成-;如果是3,则生成×,如果是4,则生成÷。拼接起来作为一个字符串。假如符号是×,生成的是
5/8×9
4.随机决定是否生成括号,假如生成(5/8×9)
5.随机决定是否重复上面1-4,直到结束。从而形成一条式子。
- 运行测试
运行演示:
出题:
对答案:
用例1:测试对答案功能:题目和答案都为空

用例2:生成一道题

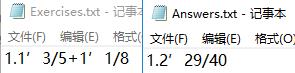
用例3:测试对答案功能:题目全是带分数形式,答案正确的9道题。
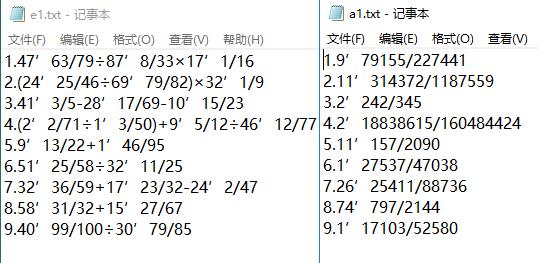

用例4:测试对答案功能:题目全是带分数形式,除了第五第九题,其余答案正确的9道题。
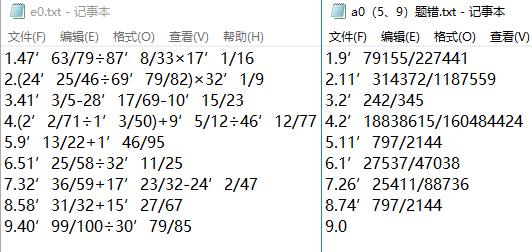

用例5:测试对答案功能:题目全是带分数形式,部分答案能化简但没化简(算作错误),其余答案正确的一万道题。
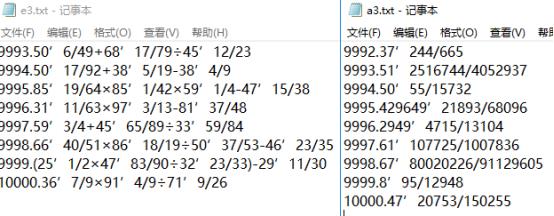

说明我们出题功能里实现的输出是符合需求的,即“真分数在输入输出时采用如下格式,真分数五分之三表示为3/5,真分数二又八分之三表示为2’3/8。”并且具有计算10000道题的能力。
用例6:生成题目全是自然数和真分数,答案正确的10道题,测试出题功能

可见我们的出题功能是符合需求的,即“真分数在输入输出时采用如下格式,真分数五分之三表示为3/5,真分数二又八分之三表示为2’3/8。”而且如第九题,能正确生成括号。
用例7:测试对答案功能:测试题目全是自然数和真分数时的对答案功能,其中答案只有前五题5个正确答案, 后五题无答案
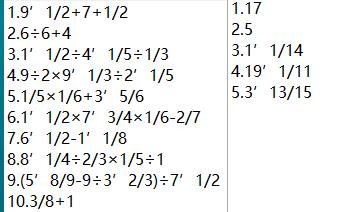

用例8:测试对答案功能:测试题目全是自然数和真分数时的对答案功能


题目是自然数和真分数的情况下也能正确检测答案正确性。
用例9:生成题目全是自然数和真分数,答案正确的10000道题,测试大量出题功能
点击出题
从开始出题提示框点击确定开始到出题完成用时1秒多。能正确生成括号。无重复题。
题目的数字不超过给定参数20。
用例10:用上述生成的10000道题,测试对答案功能
判断10000题用时和出题10000道差不多,用了1秒多的时间。
7.项目小结
通过这次的结对编程,使我们对编程有了新的认识,在双人模式下,一个人一边写代码,一边说思路,另一个人在旁听,旁听的同学通过边听边看,能发现打代码同学可能出现的一些bug进而及时修正,减少错误可能发生的概率,提升了工作效率。
同时在结对编程的过程中,对于同一个问题可能会有不同的解决办法,通过讨论,我们能得出相对较优的算法,进而提升程序的效率。
同时由于常用语言的不同,在转化方面我们更要去认真了解不同语言实现同一个函数功能之间的差异。
以上是关于结对编程(Java实现)的主要内容,如果未能解决你的问题,请参考以下文章