高中数学，复数计算，要有详细过程？

Posted 2023-04-30

参考技术A

参考技术B

本回答被提问者采纳 参考技术C

授人以鱼不如授人以渔，希望对您有帮助。

1.复数的概念

数学中规定i²=-1 (别问怎么来的问就是无中生有)

假如有 x²=-1 ,那么x=±i i为虚数单位

例题x²=-4=-1×4=i²×2²=(2i)² 其中2i为虚数［请自行理解］

以上是让你理解虚数,接下来说复数

复数z=实数+虚数 (例如 1+i,2+2i,π-2i)

其中a为实部,b为虚部(a,b属于实数).

2.复数的几何意义

小思考:实数可以放在数轴上表示,那复数呢?

①复数要在复平面上表示

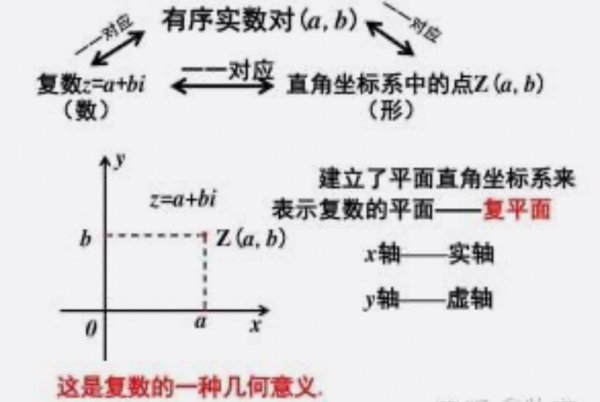
a对应x,b对应y (x轴为实轴,y为虚轴)

实数只能表示在实轴上,而复数表示在x轴外,所以可以看出复数的范围比实数大.

②复数的模

|z|=根号下a²+b²

其几何意义是:复数z在复平面内所对应的点到原点(0,0)的距离.(这里可以用向量的模理解。)

3.复数的四则运算(这里通过做题直接学会,并且会讲记忆除法的小技巧)

在此之前我们先了解一下,

共轭复数:即两个实部相等，虚部互为相反数的复数互为共轭复数。当虚部不为零时，共轭复数就是实部相等，虚部相反,如果虚部为零，其共轭复数就是自身。复数z的共轭复数记作z(头上加一横)，有时也可表示为Z*。

共轭复数

四则运算题目:设z₁=a+bi z₂=c+di

⑴求z₁+z₂= 解析:(a+c)+(b+d)i ,即实部虚部分别相加.(减法同理)

⑵求z₁·z₂= 解析:(a+bi)·(c+di)=(ac-bd)+(ad+bc)i ,即把两个复数相乘,类似乘法多项式相乘,然后展开,然后用i²=-1化简.

⑶求z₁÷z₂=

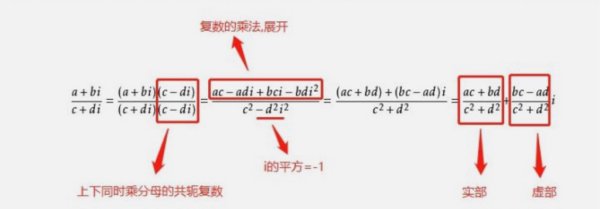
复数的除法

复数除法的记忆小技巧:

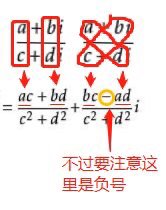
百钱百鸡，用高中数学优化算法

背景介绍

学习算法的道路上总会有各种各样的感受，偶然间碰到一个源自我国的算法问题，百钱百鸡问题，貌似很经典的问题了，可是我才刚刚知道，感觉自己太LOW了。题目是出自古代的一本叫做算经的书，原文是文言文就不往出贴了，贴了也看不懂，说大家能听懂的话就是：

有公鸡，母鸡，小鸡三种鸡，公鸡5块钱一只，母鸡三块钱一只，小鸡一块钱三只，要求用一百块钱买上面三种鸡（都要有），并且三种鸡总数是一百只，要求所有的解法。

分析

在感叹古人物价的同时，思考题目，其实很简单，只需要满足两个条件：

公鸡 + 母鸡 + 小鸡 = 100

买公鸡的钱 + 买母鸡的钱 + 买小鸡的钱 = 100

只需要满足上面两个条件即可，循环嵌套然后做判断就OK了，突然有了上大学Java期末考试时候的感觉。

写代码

因为有了上学时候的亲切感，所以就先使用Java来实现这段代码吧：

public class MoneyBuyChicken {  
  public static void main(String[] args) {

    // 定义各种鸡的价钱
    int GONG_JI = 5;
    int MU_JI = 3;
    int XIAO_JI = 1/3;

    // 100块钱最多能卖20只公鸡而且要求各种鸡都要有
    // 所以 公鸡的数量是小于20只的
    for(int i = 1; i < 20; i++) {
      // 和公鸡同理，母鸡最多的数量为33只
      for(int j = 1; j < 33; j++) {
        //计算出当前状态下小鸡的数量和剩下的钱
        int remainMoney = 100 - (i * GONG_JI + j * MU_JI);
        int xiaoJiCount = remainMoney * 3;

        // 对需要满足的条件做判断
        if(xiaoJiCount > 0 && i + j + xiaoJiCount == 100) {
          System.out.printf("公鸡%d只，母鸡%d值，小鸡%d只\\n", i, j, xiaoJiCount);
        }
      }
    }
  }
}

运行上述代码，得到结果：

公鸡4只，母鸡18值，小鸡78只

公鸡8只，母鸡11值，小鸡81只

公鸡12只，母鸡4值，小鸡84只

这在只检查结果的考试中已经OK了，交卷走人！但是，当我们看下这个算法的性能的时候，很明显就可以看到其中的问题。

上述代码使用了两层嵌套，那么它的时间复杂度为O(n^2)，这个在我们的应用中基本是不可以接受的，虽然从100只鸡中体现不出性能问题，但是如果在量级很大的地方性能问题就很明显了，所以站在学习的角度上，必须对这个进行优化。

思考

现在想想，这样的题目，貌似使我们初中奥数，或者高中数学中很常见的题目，回想当时的方法，得出了以下三元一次方程组，通过解方程组可以得到三种鸡之间的关系:

设：公鸡数量为x, 母鸡数量为y, 小鸡数量为z
则：
   5x + 3y + z/3 = 100   ①
   x + y + z = 100       ②

解：
   将①的等式两边都乘以3可以到的下列等式
   15x + 9y + z = 300    ③
   将③-②可以得到以下等式
   14x + 8y = 200
   通过上面等式进而可以得到
   y = (200 - 14x) / 8   ④
   同理将②的等式两边同时乘以3得到的等式减去①可以得到下列等式
   8z/3 - 2x = 200
   进而可以得到
   z = (600 + 6x) / 8    ⑤

至此已经得出了y(母鸡)，z(小鸡)和x(公鸡)之间的转化关系。~~（看着上面的解方程步骤感觉好亲切，虽然当时可能都不会写）

优化算法

上面我们通过数学方程的知识得到了三种鸡之间的关系，那么我们把这个结果应用到我们的代码中进行优化：

public class MoneyBuyChickenOptimize {  
  public static void main(String[] args) {

    // 定义各种鸡的价钱
    int GONG_JI = 5;
    int MU_JI = 3;
    int XIAO_JI = 1/3;

    // 100块钱最多能卖20只公鸡而且要求各种鸡都要有
    // 所以 公鸡的数量是小于20只的
    for(int i = 1; i < 20; i++) {

      // 将方程式中推导的结果带入得到各种鸡的数量
      int gongJiCount = i; // 公鸡数量
      int muJiCount = (200 - 14 * i) / 8; // 母鸡数量
      int xiaoJiCount = (600 + 6 * i) / 8; // 小鸡数量

      // 判定条件
      if(muJiCount > 0
      && xiaoJiCount > 0
      && gongJiCount + muJiCount + xiaoJiCount == 100) {
        System.out.printf("公鸡%d只，母鸡%d值，小鸡%d只\\n", gongJiCount, muJiCount, xiaoJiCount);
      }
    }
  }
}

完成，上述代码时间复杂度为O(n)，比之前的性能提升了很多，我们的目标也就达成了。

结束语

和上学时候的感觉一样，觉得学校学习的东西没有什么用；而这样一道题也一样，在工作中没有人会让写一个百钱百鸡的问题，但是我们应该从中了解到数学对于算法的帮助，在算法中有好多好的方法是不容易直接想到的，但是和这里一样，通过简单的高中数学思考一下，效果就完全不一样了。

 

---

 

本文由kenticny原创文章

转载请注明原文出处

http://www.cnblogs.com/kenticny/p/5932728.html

http://lyitlove.com/bai-qian-bai-ji-yong-gao-zhong-shu-xue-you-hua-suan-fa/