R语言初级教程(15): 矩阵（下篇）

Posted 2023-04-28

参考技术A 这是最后一篇讲解有关矩阵操作的博客，介绍有关矩阵的函数，主要有 rowSums() , colSums() , rowMeans() , colMeans() , apply() , rbind() , cbind() , row() , col() , rowsum() , aggregate() , sweep() , max.col() 。

下面通过例子来了解这些函数的用法：

我们知道，通过下标索引 [i, j] 可以访问矩阵的某一部分，索引如果没有提供意味着“所有行”或“所有列”。来看个例子，比如：

在R中，可以用一些特殊的函数来进行矩阵的行、列计算。来看些例子：

上述矩阵的行、列计算，还可以使用 apply() 函数来实现。 apply() 函数的原型为 apply(X, MARGIN, FUN, ...) ，其中： X 为矩阵或数组； MARGIN 用来指定是对行运算还是对列运算， MARGIN＝1 表示对行运算， MARGIN＝2 表示对列运算； FUN 用来指定运算函数； ... 用来指定 FUN 中需要的其它参数。来看些例子：

用 apply() 函数来实现上面的例子

apply() 函数功能很强大，我们可以对矩阵的行或列进行其它运算，例如：

如果矩阵存在 NA 值，可通过设置 na.rm=TRUE 来忽略 NA 值，然后再计算。比如：

甚至我们还可以自定义运算函数，来看个例子：

在R中， rbind() 和 cbind() 函数可分别为矩阵添加行和列，来看一个例子：

在R中， row() 和 col() 函数将分别返回元素的行和列下标矩阵，来看个例子：

通过这两个函数，可以获取矩阵的对角元素以及上下三角矩阵，例如：

有时，你可能需要对每行进行分组，然后组内每列求和。在R中可以用 rowsum() 函数来解决，而且效率也非常高。先看个例子：

你也可以用 aggregate() 函数获得类似结果：

有人就会问“为啥没有列分组求和的操作？”，其实你可以先将矩阵转置，然后行分组求和；这两步就等同于列分组求和。

sweep() 函数的原型为 sweep(x, MARGIN, STATS, FUN = "-", check.margin = TRUE, ...) ，其中： x 为矩阵或数组； MARGIN 用来指定是对行运算还是对列运算， MARGIN＝1 表示对行运算， MARGIN＝2 表示对列运算； STATS 表示想要清除的统计量； FUN 用来指定运算函数，默认为减法 - ； check.margin 用来核实 x 的维度是否与 STATS 的匹配，如果事先知道它们匹配的话，将其设为 FALSE 将提高运算速度； ... 用来指定 FUN 中需要的其它参数。来看些例子：

事实上，通过改变 FUN 参数的具体形式或自定义函数， sweep() 函数可以实现很多不同操作，这里就不细讲了。

max.col() 函数返回矩阵每行最大值所在的列位置（即列下标），其原型为 max.col(m, ties.method = c("random", "first", "last")) ，其中： m 为矩阵；当存在多个最大值时， ties.method 指定用哪种方式来处理这种情况，默认为"random"（随机），"first"指使用第一个最大值，"last"指使用最后一个最大值。来看个官网例子：

我们也可以结合 apply() 和 which.max() 函数来实现 max.col(mm, 'first') 。看个例子，

R矩阵的最后一部分内容就讲到这。

如若有遗漏，后期将会添加至本博客。

R语言基础入门—矩阵介绍

上一期给大家介绍了R语言几个基本概念：R语言基础入门—常量、变量与数据结构介绍，今天继续给大家介绍R语言—矩阵，希望对您的R语言学习有所帮助。

矩阵

矩阵是其中元素以二维矩形布局布置的R对象， 它们包含相同原子类型的元素。 这种数据结构很类似于其它语言中的二维数组，但 R 提供了语言级的矩阵运算支持。

矩阵里的元素可以是数字、符号或数学式。

一个 M x N 的矩阵是一个由 M（row） 行 和 N 列（column）元素排列成的矩形阵列。

以下是一个由 6 个数字元素构成的 2 行 3 列的矩阵：

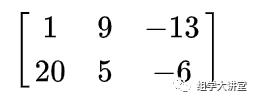
矩阵创建

R 语言的矩阵可以使用 matrix() 函数来创建，语法格式如下：

matrix(data = NA, nrow = 1, ncol = 1, byrow = FALSE,dimnames = NULL)

参数说明：

• data 向量，矩阵的数据

• nrow 行数

• ncol 列数

• byrow 逻辑值，为 FALSE 按列排列，为 TRUE 按行排列

• dimname 设置行和列的名称

创建一个数字矩阵“

# byrow 为 TRUE 元素按行排列
M <- matrix(c(3:14), nrow = 4, byrow = TRUE)
print(M)

# Ebyrow 为 FALSE 元素按列排列
N <- matrix(c(3:14), nrow = 4, byrow = FALSE)
print(N)

# 定义行和列的名称
rownames = c("row1", "row2", "row3", "row4")
colnames = c("col1", "col2", "col3")

P <- matrix(c(3:14), nrow = 4, byrow = TRUE, dimnames = list(rownames, colnames))
print(P)

执行以上代码输出结果为：
[,1] [,2] [,3]
[1,]    3    4    5
[2,]    6    7    8
[3,]    9   10   11
[4,]   12   13   14
     [,1] [,2] [,3]
[1,]    3    7   11
[2,]    4    8   12
[3,]    5    9   13
[4,]    6   10   14
     col1 col2 col3
row1    3    4    5
row2    6    7    8
row3    9   10   11
row4   12   13   14

转置矩阵

R 语言矩阵提供了 t() 函数，可以实现矩阵的行列互换。

例如有个 m 行 n 列的矩阵，使用 t() 函数就能转换为 n 行 m 列的矩阵。

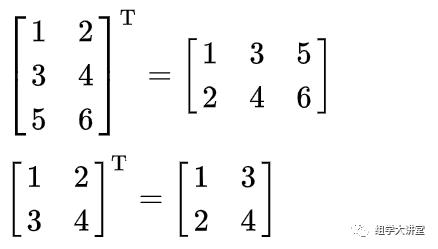
# 创建一个 2 行 3 列的矩阵
M = matrix( c(2,6,5,1,10,4), nrow = 2,ncol = 3,byrow = TRUE)
print(M)
     [,1] [,2] [,3]
[1,]    2    6    5
[2,]    1   10    4
# 转换为 3 行 2 列的矩阵
print(t(M))

执行以上代码输出结果为：
     [,1] [,2] [,3]
[1,]    2    6    5
[2,]    1   10    4
 "-----转置后-----"
     [,1] [,2]
[1,]    2    1
[2,]    6   10
[3,]    5    4

矩阵有一个dim属性，内容是两个元素的向量， 两个元素分别为矩阵的行数和列数。dim属性可以用dim()函数访问。如

# 创建一个 2 行 3 列的矩阵
M = matrix( c(2,6,5,1,10,4), nrow = 2,ncol = 3,byrow = TRUE)
print(M)
     [,1] [,2] [,3]
[1,]    2    6    5
[2,]    1   10    4

dim(A)
[1] 2 3

访问矩阵元素

如果想获取矩阵元素，可以通过使用元素的列索引和行索引，类似坐标形式。

# 定义行和列的名称
rownames = c("row1", "row2", "row3", "row4")
colnames = c("col1", "col2", "col3")

# 创建矩阵
P <- matrix(c(3:14), nrow = 4, byrow = TRUE, dimnames = list(rownames, colnames))
print(P)
# 获取第一行第三列的元素
print(P[1,3])

# 获取第四行第二列的元素
print(P[4,2])

# 获取第二行
print(P[2,])

# 获取第三列
print(P[,3])

执行以上代码输出结果为：

     col1 col2 col3
row1    3    4    5
row2    6    7    8
row3    9   10   11
row4   12   13   14

[1] 5

[1] 13

 col1 col2 col3 
    6    7    8 

 row1 row2 row3 row4 
    5    8   11   14 

矩阵计算

大小相同（行数列数都相同）的矩阵之间可以相互加减，具体是对每个位置上的元素做加减法。矩阵的乘法则较为复杂。两个矩阵可以相乘，当且仅当第一个矩阵的列数等于第二个矩阵的行数。

矩阵加减法

# 创建 2 行 3 列的矩阵
matrix1 <- matrix(c(7, 9, -1, 4, 2, 3), nrow = 2)
print(matrix1)

matrix2 <- matrix(c(6, 1, 0, 9, 3, 2), nrow = 2)
print(matrix2)

# 两个矩阵相加
result <- matrix1 + matrix2
cat("相加结果：","\n")
print(result)

# 两个矩阵相减
result <- matrix1 - matrix2
cat("相减结果：","\n")
print(result)

执行以上代码输出结果为：

     [,1] [,2] [,3]
[1,]    7   -1    2
[2,]    9    4    3
     [,1] [,2] [,3]
[1,]    6    0    3
[2,]    1    9    2
相加结果： 
     [,1] [,2] [,3]
[1,]   13   -1    5
[2,]   10   13    5
相减结果： 
     [,1] [,2] [,3]
[1,]    1   -1   -1
[2,]    8   -5    1

矩阵乘除法

# 创建 2 行 3 列的矩阵
matrix1 <- matrix(c(7, 9, -1, 4, 2, 3), nrow = 2)
print(matrix1)

matrix2 <- matrix(c(6, 1, 0, 9, 3, 2), nrow = 2)
print(matrix2)

# 两个矩阵相乘
result <- matrix1 * matrix2
cat("相乘结果：","\n")
print(result)

# 两个矩阵相除
result <- matrix1 / matrix2
cat("相除结果：","\n")
print(result)
执行以上代码输出结果为：

     [,1] [,2] [,3]
[1,]    7   -1    2
[2,]    9    4    3
     [,1] [,2] [,3]
[1,]    6    0    3
[2,]    1    9    2
相乘结果： 
     [,1] [,2] [,3]
[1,]   42    0    6
[2,]    9   36    6
相除结果： 
         [,1]      [,2]      [,3]
[1,] 1.166667      -Inf 0.6666667
[2,] 9.000000 0.4444444 1.5000000

报道热点资讯  解读前沿进展 分享科研资料  

微信加群

我们组建了20余个交流群、资料分享群，欢迎大家进群交流。添加公众号博主微信：mBioMan（下方二维码），邀你进群。温馨提示：添加博主时，请备注一下研究方向+单位/学校！

转载、合作、广告请联系微信mBioMan

在看，也是一种习惯