线性模型

Posted 2023-04-25

参考技术A

这一篇的内容旨在对之前学习过的四种不同线性分类模型（ Logistic 回归、softmax回归、感知器和支持向量机 ）做一个整理。这些模型的区别主要在于使用了不同的损失函数。

线性模型（Linear Model）是机器学习中应用最广泛的模型，指通过样本特征的线性组合来进行预测的模型。给定一个 维样本 ，其线性组合函数为：

其中 为 维的权重向量， 为偏置。线性回归就是典型的线性模型，直接用 来预测输出目标 。

在分类问题中，由于输出 是一些离散的标签， 的值域为实数，因此无法直接用 来进行预测，需要引入一个 非线性的决策函数（Decision Function） 来预测输出目标：

其中 也称为 判别函数（Discriminant Function） 。

也就是说，一个线性分类模型（Linear Classification Model）或线性分类器（Linear Classifier），是由一个（或多个）线性的判别函数 和非线性的决策函数 组成。

二分类（Binary Classification）的类标签 只有两种取值，通常可设为 。

在二分类中我们只需要一个线性判别函数 。所有满足 的点组成一个分割超平面（Hyperplane），称为决策边界（Decision Boundary）或决策平面（Decision Surface）。决策边界将特征空间一分为二，划分成两个区域，每个区域对应一个类别。

线性模型试图学习到参数 ，使得对于每个样本 尽量满足：

上面两个公式也可以合并，即参数 尽量满足：

接下来我们会看到，对线性模型来说， 这一表达式是十分重要的。

于是我们可以定义： 对于训练集 ，若存在权重向量 ，对所有样本都满足 ，那么训练集 是线性可分的 。

接下来我们考虑多分类的情形，假设一个多类分类问题的类别为 ，常用的方式有以下三种：

若存在类别 ，对所有的其他类别 ，都满足 ，那么 属于类别 。即：

“一对其余”和“一对一”都存在一个缺陷：特征空间中会存在一些难以确定类别的区域，而“argmax”方式很好地解决了这个问题 。下图给出了用这三种方式进行三类分类的示例，其中不同颜色的区域表示预测的类别，红色直线表示判别函数 的直线。在“argmax”方式中，类 和类 的决策边界实际上由 决定，其法向量为 。

在本节中我们采用 以符合Logistic 回归的描述习惯。

为解决连续线性函数不适合进行分类的问题，我们引入非线性函数 来预测类别标签的后验概率 ：

其中 通常称为 激活函数（Activation Function） ，其作用是把线性函数的值域从实数区间“挤压”到了 之间，可以用来表示概率。

在Logistic回归中，我们使用Logistic函数来作为激活函数。标签 的后验概率为：

标签 的后验概率为：

进行变换后得到：

其中 为样本 为正反例后验概率的比值，称为 几率（Odds） ，几率的对数称为对数几率。因此，Logistic 回归也称为 对数几率回归（Logit Regression） 。

Logistic回归采用交叉熵作为损失函数，并使用梯度下降法来对参数进行优化。 其风险函数为：

风险函数 是关于参数 的连续可导的凸函数。因此Logistic回归除了梯度下降法之外还可以用高阶的优化方法，比如牛顿法，来进行优化。

Softmax回归，也称为多项（multinomial）或多类（multi-class）的Logistic回归，是 Logistic回归在多类分类问题上的推广 。

对于多类问题，类别标签 可以有 个取值。给定一个样本x，Softmax回归预测的属于类别 的条件概率为：

其中 是第 类的权重向量。

Softmax回归的决策函数可以表示为：

给定 个训练样本 ， Softmax回归使用交叉熵损失函数来学习最优的参数矩阵 。

采用交叉熵损失函数，Softmax回归模型的风险函数为：

风险函数 关于 的梯度为：

采用梯度下降法，Softmax回归的训练过程为：

感知器可谓是最简单的人工神经网络，只有一个神经元。

感知器是一种简单的两类线性分类模型，其分类准则为：

给定N 个样本的训练集： ，其中 ，感知器学习算法试图找到一组参数 ，使得对于每个样本 有

感知器的学习算法是一种错误驱动的在线学习算法，先初始化一个权重向量 （通常是全零向量），然后每次分错一个样本 时，即 ，就用这个样本来更新权重：

根据感知器的学习策略，可以反推出 感知器的损失函数 为：

采用随机梯度下降，其每次更新的梯度为：

感知器收敛性不再证明，参考之前的笔记 https://www.jianshu.com/p/d83aa6c8068f 。

感知器的学习到的权重向量和训练样本的顺序相关。 在迭代次序上排在后面的错误样本，比前面的错误样本对最终的权重向量影响更大 。比如有1000个训练样本，在迭代100个样本后，感知器已经学习到一个很好的权重向量。在接下来的899个样本上都预测正确，也没有更新权重向量。但是在最后第1000 个样本时预测错误，并更新了权重。这次更新可能反而使得权重向量变差。

为了改善这种情况，可以使用“参数平均”的策略来提高感知器的鲁棒性，也叫 投票感知器 （投票感知器是一种集成模型）。

投票感知器记录第 次更新后得到的权重 在之后的训练过程中正确分类样本的次数 。这样最后的分类器形式为：

投票感知器虽然提高了感知器的泛化能力，但是需要保存 个权重向量。在实际操作中会带来额外的开销。因此，人们经常会使用一个简化的版本，也叫做平均感知器：

其中 为平均的权重向量。

给定N 个样本的训练集： ，其中 ，如果两类样本是线性可分的，即存在一个超平面：

将两类样本分开，那么对于每个样本都有 。

数据集 中每个样本 到分割超平面的距离为：

定义整个数据集 中所有样本到分割超平面的最短距离为间隔（Margin） ：

如果间隔 越大，其分割超平面对两个数据集的划分越稳定，不容易受噪声等因素影响。支持向量机的目标是寻找一个超平面 使得 最大，即：

令 ，则上式等价于：

数据集中所有满足 的点，都称为 支持向量 。

接下来的推导不详细叙述了，之前的笔记里已经记录过。

软间隔的优化问题形式如下：

其中 称为 Hinge损失函数 。 可以看作是正则化系数。

其实这一节才是整理的关键，有助于厘清各个分类器之间的联系。

线性混合模型——广义线性模型

我们知道，混合线性模型是一般线性模型的扩展，而广义线性模型在混合线性模型的基础上又做了进一步扩展，使得线性模型的使用范围更加广阔。每一次的扩展，实际上都是模型适用范围的扩展，一般线性模型要求观测值之间相互独立、残差(因变量)服从正态分布、残差(因变量)方差齐性，而混合线性模型取消了观测值之间相互独立和残差(因变量)方差齐性的要求，接下来广义线性模型又取消了对残差(因变量)服从正态分布的要求。残差不一定要服从正态分布，可以服从二项、泊松、负二项、正态、伽马、逆高斯等分布，这些分布被统称为指数分布族，并且引入了连接函数，根据不同的因变量分布、连接函数等组合，可以得到各种不同的广义线性模型。

要注意，虽然广义线性模型不要求因变量服从正态分布，但是还是要求相互独立的，如果不符合相互独立，需要使用后面介绍的广义估计方程。

=================================================
一、广义线性模型

广义线性模型的一般形式为：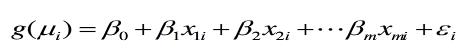

有以下几个部分组成

1.线性部分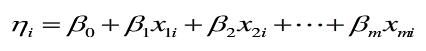

2.随机部分ε_i

3.连接函数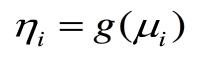

连接函数为单调可微(连续且充分光滑)的函数，连接函数起了"y的估计值μ"与"自变量的线性预测η"的作用，在一般线性模型中，二者是一回事，但是当自变量取值范围受限时，就需要通过连接函数扩大取值范围，因此在广义线性模型中，自变量的线性预测值是因变量的函数估计值。

广义线性模型设定因变量服从指数族概率分布，这样因变量就可以不局限于正态分布一种形式，并且方差可以不稳定。

指数分布族的概率密度函数为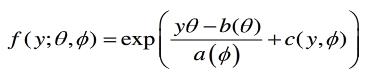

其中θ和φ为两个参数，θ为自然参数，φ为离散参数，a,b,c为函数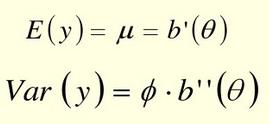

广义线性模型的参数估计：

广义线性模型的参数估计一般不能使用最小二乘法，常用加权最小二乘法或极大似然法。回归参数需要用迭代法求解。

广义线性模型的检验和拟合优度：

广义线性模型的检验一般使用似然比检验、Wald检验。模型的比较用似然比检验，回归系数使用Wald检验。

似然比检验是通过比较两个相嵌套模型(如模型P嵌套在模型K内)的对数似然函数来进行的，其统计量为G：

G=-2*(lp-lk)

lp是模型P的对数似然函数，lk是模型k1的对数似然函数

模型P中的自变量是模型K中自变量的一部分，另一部分就是要检验的变量，这里G服从自由度为K-P的卡方分布。

广义线性模型的拟合优度通常使用以下统计量来度量:

离差统计量，pearson卡方统计量，AIC,AICC,BIC,CAIC准则，准则的值越小越好