二项分布概率最大项K的求法公式 k=(n+1)p是怎么推导的？

Posted 2023-04-25

已知X~B(n,p)，则要使 P(x=k0）最大，结果如下：
当（n+1)p 为整数时，k0=(n+1)p,或 k0=(n+1)p-1
当（n+1)p 不是整数时，k0=[(n+1)p] （[]表示取整） 请问这个公式是怎么推出来的啊？

用比值法就可以。

P(X=k) / P(X=k-1) = (n-k+1) p / k (1-p)。

所以当（n-k+1) p > k (1-p)，也就是k < (n+1)p时，P(X=k) / P(X=k-1) > 1。

也就是当k < (n+1)p时，P(X=k)单调增。

所以最大值是：k = (n+1)p向下取整。

定义

在概率论和统计学中，二项分布是n个独立的成功／失败试验中成功的次数的离散概率分布，其中每次试验的成功概率为p。这样的单次成功／失败试验又称为伯努利试验。实际上，当n=1时，二项分布就是伯努利分布。

参考技术A

简单计算一下即可，答案如图所示

参考技术B 用比值法就可以。
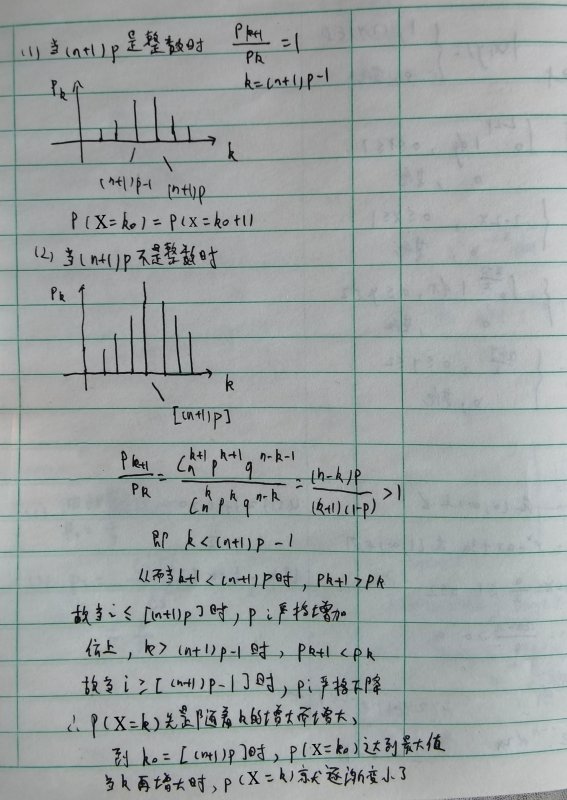
P(X=k) / P(X=k-1) = (n-k+1) p / k (1-p)
所以当 (n-k+1) p > k (1-p)，也就是 k < (n+1)p 时，P(X=k) / P(X=k-1) > 1
也就是当 k < (n+1)p 时，P(X=k) 单调增。
所以最大值是：k = (n+1)p 向下取整本回答被提问者和网友采纳

二项分布（Binomial Distribution）

1.二项分布的基本描述：

　　二项分布就是重复n次独立的伯努利实验。伯努利实验就是在同样的条件下重复发生、且每次实验相互独立的一种随机试验。二项分布有两个参数n和p，n是重复实验的次数，p是每次独立实验发生的概率。特殊的n=1时，我们把二项分布称为伯努利分布。

　　N次独立重复试验中发生K次的概率是：

　　P(ξ=K)= C(n,k) * p^k * (1-p)^(n-k)，其中C(n, k) =n!/(k!(n-k)!)，注意：第二个等号后面的括号里的是上标，表示的是方幂。

　　那么就说这个属于二项分布。其中P称为成功概率。记作ξ~B(n,p)

　　期望：Eξ=np；

　　方差：Dξ=npq；　　其中q=1-p