卷积层在神经网络中如何运算？

Posted 2023-04-23

参考技术A

卷积神经网络（Convolutional Neural Networks, CNN）的核心是进行卷积运算操作。在实际应用中往往采用多层网络结构，因此又被称为深度卷积神经网络。本文将从单个卷积的计算出发，带大家掌握卷积层在神经网络中的运算方法。

2.1 单个卷积的计算

要想了解卷积层在神经网络中的计算过程，我们首先需要了解单个“卷积”是如何运作的。

想必大家在学习CNN的过程中都见过下图（ 出处在此 ，这上面有各种各样的卷积gif图）：

input_shape=(5,5)，kernelsize=(3,3)，padding=‘same’，stride=1，output_shape=(5,5)

在此图中：

在此次计算中：

Ps： 在实际应用中，每一个输出的特征图还会配备一个偏置bais，在上图中无表示。

2.2 卷积层在神经网络中的运算

了解完单个卷积是如何计算的之后，我们就可以从神经网络的角度来看‘卷积层’的运算过程了。下图展示的是输入三通图像（8*8*3）经一层卷积结构，输出两通特征图（8*8*2）的计算过程：

卷积参数：input_shape=(8,8,3)，kernelsize=(3,3)，padding=‘same’，stride=1，output_shape=(8,8,2)

在此图中：

在此次卷积层的运算中：

首先我们来关注一下输入和输出，他俩的尺度都是（8*8），而输入是3通道，输出是2通道（深度学习中不管干啥一定要先看输入输出，对一层是这样，对整个模型也是这样）。

其次就准备进入我们最熟悉的卷积核计算了，可是在此之前我们得知道，这个运算过程中到底发生了几次卷积核计算呢？有的朋友可能要说，卷积的一大特性就是‘权值共享’，有几通输出就有几个卷积核，每个卷积核把输入特征图从头扫到尾。然而这个其实是不对的！

实际上，在卷积核计算数量问题上，应该是“ 有几通道的输出就有几套卷积核，每套内的卷积核数量与输入通道数相等 ”，就像我在上图中所画的：

至此，这一个卷积层的运算就全部完成了。

2.3 “可训练参数”验证

毕竟空口无凭，下面我来通过“ 可训练参数 ”的数量，来为大家验证一下卷积层是不是按我说的这么运算的。大家应该知道，一个卷积层内的“可训练参数”，其实就是指的卷积核里的那些值，以及要加的偏置量，那么如果按照前面描述的计算方法来看，一个卷积层内的“可训练参数有多少呢”？我们可知：

由此可得到：

那么按理说可训练参数量应为：

让我们用keras的summary()来验证一下：

很棒！

记住，普通卷积层的可训练参数量为：

Ps： 还有一个衡量模型大小、复杂度的量叫做“理论计算量FLOPs”（floating point operations）。它通常只考虑Conv、FC等参数层的乘、加操作的数量，并且“纯加”操作也会被忽略（例如bias）。卷积层运算中的FLOPs计算公式为：

Ps： 这里还要为大家明确一个“感受野”的概念，简单来讲就是卷积神经网络中的某一层特征图上的一个点，对应到原图上可以关联到多少个点，我们用一张图来解释一下：

上图展示的是一个3层一维卷积，kernel_size=3，我们可以看到：顶层左一的像素与底层左起7个像素值有关，这时候就代表它的感受野有7。我们可以显而易见的得出以下两个结论：

这个感受野在后续的卷积的拆分讲解中还要用到。

卷积神经网络初识

    卷积神经网络是基本的一种运算，多用于来处理和矩阵有关的对象，如二维数组形式储存的图片等！

1.卷积运算初识：
    卷积运算是两个矩阵运算所得，主要是相乘（和真正线性代数中的乘不一样，如下图所示）

图1 卷积图运算图示

图中浅蓝色九宫格和被覆盖的无色格子矩阵相乘（每个格子里面有一个数字），乘后数字和为深蓝色格子中值。依次覆盖，让浅蓝色格子覆盖完空白格子，可以得到：

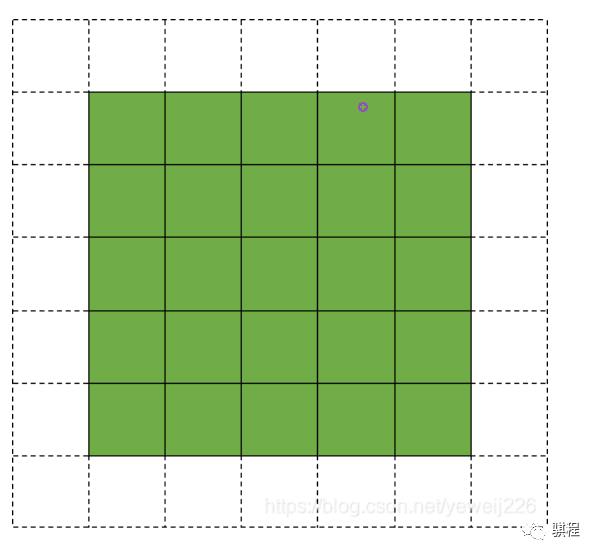
图2 卷积计算后

    卷积运算主要适应于图片处理（含视频处理），处理后有高斯模糊、梦境效果等诸多效果。

    

2.演示：
主要运算演示如下：

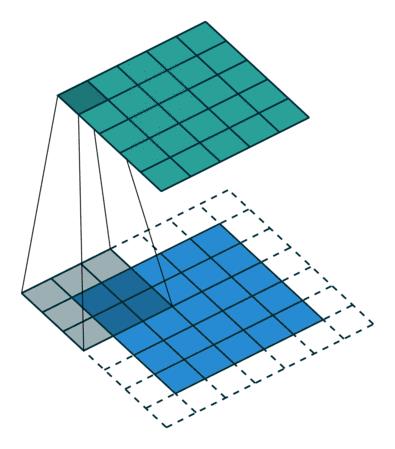
图3 卷积运算演示图

顺便可以看下代码的具体卷积操作：

//卷积运算实例（运算后结果为一个2*2矩阵）

public class jjstraight {
    public static void main(String[] args) {
        //测试数组
        int[][] img = new int[][] {{6,1,3,5},{4,6,8,2},{4,8,8,6},{5,6,8,2}};
        //卷积核
        int[][] kArray = {{-1,-1,-8},{-1,25,-1},{-1,1,-1}};
        //卷积之后数组
        int width =img.length-kArray.length+1;
        int height = img[0].length-kArray[0].length+1;
        int[][] ima = new int[width][height];
        for(int i=0;i<width;i++) {
            for(int j = 0;j<height;j++) {
                for(int m =0;m < kArray.length;m++) {
                    for(int n = 0;n<kArray.length;n++) {
                        ima[i][j] =  (int)((img[i+m][j+n])*kArray[m][n]);
                    }
                }
            }
        }
        for(int i=0; i<ima.length; i++) {
            System.out.println(Arrays.toString(ima[i]));
        }
    }
}

图4 运算后结果

3.问题处理：
    从上面的演示能够看出会有边缘最后一圈的像素点没有卷积运算中的值，那么就会有几种常见的办法处理图像边缘

     ① 不管边缘：就是如果边缘占比足够小而且对输出结果没啥影响时的操作）

     对图像而言，像素特别多，最外一圈没有特殊要求不做处理也可以，对图片几乎没有视觉观看影响，但对机器的显示和处理是有影响的。
      ②直接舍掉边缘未处理区域：也就是说输出的只有绿色部分，当然这种办法无法输出全部图像，因而很少使用
     ③填充周围：使用一些假像素（通常是0）来填充边缘，从而产生与输入相同大小的输出。
    ④步幅增大：使用更大的滑动步幅，常见于图像缩小时（池化）的操作，这里不再赘述
  
    通过边缘的处理，我们最终会得到处理后的图像数据，特征提取完成，输出即可完成特征映射，如演示中所示！

    二维卷积常见于灰度图的操作！