数据包络分析的DEA模型

Posted 2023-04-23

参考技术A

DEA是一个线性规划模型，表示为产出对投入的比率。通过对一个特定单位的效率和一组提供相同服务的类似单位的绩效的比较，它试图使服务单位的效率最大化。在这个过程中，获得100%效率的一些单位被称为相对有效率单位，而另外的效率评分低于100%的单位被称为无效率单位。
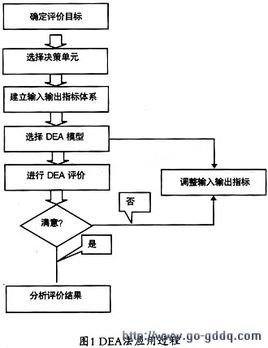
这样，企业管理者就能运用DEA来比较一组服务单位，识别相对无效率单位，衡量无效率的严重性，并通过对无效率和有效率单位的比较，发现降低无效率的方法。 DEA线形规划模型建立如下：
1) 定义变量
设Ek（k=1，2，……， K）为第k个单位的效率比率，这里K代表评估单位的总数。
设uj（j=1，2，……， M）为第j种产出的系数，这里M代表所考虑的产出种类的总数。变量uj用来衡量产出价值降低一个单位所带来的相对的效率下降。
设vI（I=1，2，……，N）为第I种投入的系数，这里N代表所考虑的投入种类的总数。变量vI用来衡量投入价值降低一个单位带来的相对的效率下降。
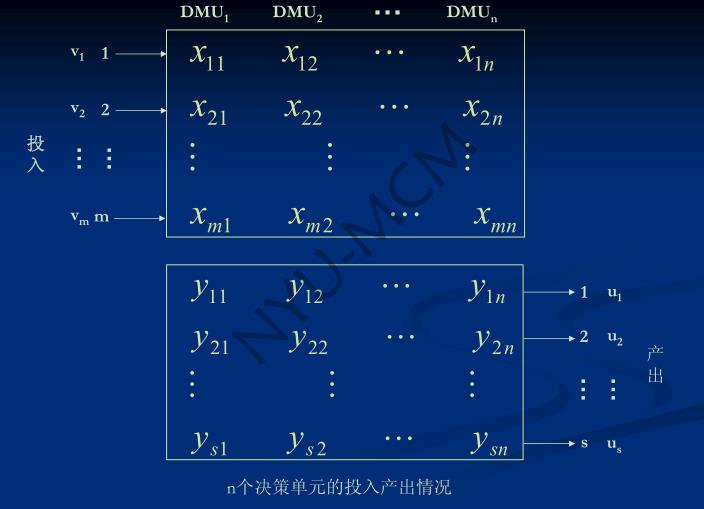
设Ojk为一定时期内由第k个服务单位所创造的第j种产出的观察到的单位的数量。
设Iik为一定时期内由第k个服务单位所使用的第i种投入的实际的单位的数量。
2) 目标函数
目标是找出一组伴随每种产出的系数u和一组伴随每种投入的系数ν，从而给被评估的服务单位最高的可能效率。（*）
式中，e是被评估单位的代码。这个函数满足这样一个约束条件，当同一组投入和产出的系数（uj和vi）用于所有其他对比服务单位时，没有一个服务单位将超过100%的效率或超过1.0的比率。
3) 约束条件（**）
k=1,2,……,K
式中所有系数值都是正的且非零。
为了用标准线性规划软件求解这个有分数的线性规划，需要进行变形。要注意，目标函数和所有约束条件都是比率而不是线性函数。通过把所评估单位的投入人为地调整为总和1.0，这样等式（*）的目标函数可以重新表述为：满足以下约束条件：对于个服务单位，等式（**）的约束条件可类似转化为：k=1,2,…,K
式中 uj≥0 j=1，2，…，M vi≥0 i=1，2，…，N 关于服务单位的样本数量问题是由在分析种比较所挑选的投入和产出变量的数量所决定的。下列关系式把分析中所使用的服务单位数量K和所考虑的投入种类数N与产出种类数M联系出来，它是基于实证发现和DEA实践的经验：

参考技术B 《红楼梦》是一部内涵丰厚的作品，《好了歌》和十二支《红楼梦曲》提示着贾宝玉所经历的三重悲剧。作者将贾宝玉和一群身份、地位不同的少女放在大观园这个既是诗化的、又是真实的小说世界里，来展示她们的青春生命和美的被毁灭的悲剧。作品极为深刻之处在于，并没有把这个悲剧完全归于恶人的残暴，其中一部分悲剧是封建势力的直接摧残，如鸳鸯、晴雯、司棋这些人物的悲惨下场，但是更多的悲剧是封建伦理关系中的“通常之道德、通常之人情、通常之境遇”所造成的，是几千年积淀而凝固下来的正统文化的深层结构造成的人生悲剧。小说描绘了上至皇宫、下及乡村的广阔历史画面，广泛而深刻地反映了封建末世复杂深刻的矛盾冲突，显示了封建贵族的本质特征和必然衰败的历史命运。尤其深刻的是，在小说展示的贾府的生活图画里，显示出维持着这个贵族之家的等级、名分、长幼、男女等关系的礼法习俗的荒谬，揭开了封建家族“温情脉脉面纱”内里的种种激烈的矛盾和斗争。

数学建模 数据包络分析(DEA) Lingo实现

 

model:
sets:
dmu/1..7/:lambda;     !决策单元;
inw/1..4/:s1;         !投入变量集;
outw/1..4/:s2;        !产出变量集;
inv(inw, dmu):x;      !投入数据;
outv(outw, dmu):y;    !产出数据;
endsets

data:
n=?;                  !所评价的决策单元;
x= 349.3313 0.63114 5.59091 6.30942 3.84352 0.50472 37.86518   !AZ;
   1620.7 1.2335 17.19304 25.30626 251.4798 44.21377 117.4841  !CA;
   75.48889 0.06826 1.51314 6.75239 1.04937 0.08122  40.8765   !NM; 
   1169.069 1.27549 15.62031 9.99996 9.71338 80.82566 57.3492; !TX;

!消耗*价格;
y= 19110.63 34.52749 305.8581 14526.70504576 3843.5218771 2188.06567 89941.053949  !AZ;
   80799.65 61.49606 857.1551 39765.719738 251479.771641 70912.239599 279059.7185637
   4030.339 3.64439 80.78612  16038.926614 1049.366891 1043.89315 97093.81923952
   65780.31 71.76835 878.9118 22339.449732 9713.3800554 121621.9387228 146673.1547010;
enddata

min=theta;        
@for(inw(i):@sum(dmu(j)|j#ne#n:lambda(j)*x(i,j))+s1(i)=theta*x(i,n)); !输入约束;
@for(outw(i):@sum(dmu(j)|j#ne#n:lambda(j)*y(i,j))-s2(i)=y(i,n));  !输出约束;
a = @sum(dmu(j):lambda(j))/theta;  !规模有效性;
end