如何用matlab求解二阶微分方程，以及程序实例

Posted 2023-04-22

1、对于求数值解的微分方程，你可以用ode45()函数求解。如求下列微分方程

func。m   %自定义微分方程的函数

function z = func(t,y)

z =[y(2);(1-y(1)^2)*y(2)-y(1)];

main。m  %主程序

clear all;close all;clc

y0 = [0.25;0];

h = 0.1;

a = 0;

b = 20;

[t1 y1] = ode45(@func,y0,h,a,b)

2、对于求解析解的微分方程，你可以用dsolve()函数求解。如求微分方程x*y''+x﹡(y')^2-y'=0的解析解,可以下列步骤计算

>> syms y(x)

>>Dy = diff(y)；D2y = diff(y, 2)；

>>dsolve(x*D2y+x*(Dy)^2-Dy==0,'x')

参考技术A

1、首先看一下matlab求解方程的方法，首先指明所解方程的变量，然后指明方程，未知数和限制条件，最后求解方程。

2、在matlab命令行窗口中输入syms x [x,params,conds]=solve(sin(x)==1,'ReturnConditions', true) ，按回车键可以得到方程解。

3、转换一下，可以看到sin(x)=1方程的解是如下图所示 。

4、也可以求解下面的一个方程。

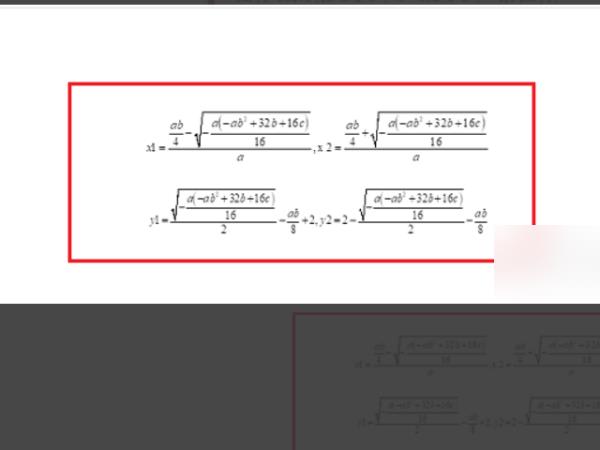
5、输入syms a b c y x；[x,y]=solve([a*x^2+b*y+c==0,a*x+2*y==4],[x,y])。

6、按回车键可以得到方程解。

参考技术B dsolve('D2y=x','x')
ans
=
x^3/6
+
C2*x
+
C3
D2y的意思就是y的二阶微分项
不明白你的问题什么意思，要输入的话直接定义符号变量输入
syms
D2x
x
D2x=x;
如果是矩阵，那就用矩阵表示

使用 MATLAB 求解二阶微分方程组

【中文标题】使用 MATLAB 求解二阶微分方程组

【英文标题】：Solving a system of second order differential equations using MATLAB

【发布时间】：2022-01-04 12:04:24

【问题描述】：

我正在尝试解决弹丸运动问题，以确定在给定初始条件下的起飞速度，该问题被简化为两个二阶微分方程组。我的代码和问题在下面的图片中。问题方程中的常数值已简化为常数a、b、c 和d。

x¨(t)=-1/2m ρAC_d cos⁡(arctan⁡((y˙(t))/(x˙(t) )))(〖x˙(t)〗^2+ 〖y˙(t)〗^2)
y¨(t)=-1/2m(2mg+ρAC_d sin⁡(arctan⁡((y˙(t))/(x˙(t) )))(〖x˙(t)〗^2+ 〖y˙(t)〗^2)

# With the initial conditions:

x˙(0)=cosθ ∙ V_0

y˙(0)=sinθ ∙ V_0

x(0)=0

y(0)=0

我的解决方案代码如下所示；

syms x(t) y(t) a b c d u theta
% Equations
% d2x = -a*cos(arctan(dy/dx))*(((dx)^2)+(dy)^2));
% d2y = -b*(c + d*sin(arctan(dy/dx))*(((dx)^2)+(dy)^2));

%Constants
dx=diff(x,t);
dy=diff(y,t);
d2x=diff(x,t,2);
d2y=diff(y,t,2);
a=1;
b=2;
c=3;
d=4;

%Initial Conditions

cond1 = x(0) == 0;
cond2 = y(0) == 0;
cond3 = dx(0) == u*cos(theta);
cond4 = dy(0) == u*sin(theta);

conds = [cond1 cond2 cond3 cond4];

eq1 = -a*cos(atan(dy/dx))*(((dx)^2)+(dy)^2);
eq2 = -b*(c + d*sin(atan(dy/dx))*(((dx)^2)+(dy)^2));

vars = [x(t); y(t)];
V = odeToVectorField([eq1,eq2]);
M = matlabFunction(V,'vars', 't','Y');
interval = [0 5];  %time interval    
ySol = ode23(M,interval,conds);

错误信息如下所示；

Error using mupadengine/feval (line 187)
System contains a nonlinear equation in 'diff(y(t), t)'. The system must be quasi-linear:
highest derivatives must enter the differential equations linearly.

Error in odeToVectorField>mupadOdeToVectorField (line 189)
T = feval(symengine,'symobj::odeToVectorField',sys,x,stringInput);

Error in odeToVectorField (line 138)
sol = mupadOdeToVectorField(varargin);

Error in velocity_takeoff (line 29)
V = odeToVectorField([eq1,eq2]);

为什么会出现这些错误以及如何缓解这些错误？

【参考方案1】：

这看起来不太理想。不需要三角函数，尤其是在使用的形式中，它们可能会引入符号错误，请使用atan2 来避免这种情况。方程是简化的形式

as vectors dv/dt = -g*e_2 - k*speed*v, where speed = |v| is the norm of the vector
and additionally dxy/dt=v,  xy=[x,y] being the position vector

在组件中实现，这给了

function du_dt = motion(t,u)
  x=u(1); y=u(2); vx=u(3); vy=u(4);
  speed = hypot(vx,vy);
  ax = -k*speed*vx;
  ay = -k*speed*vy - g;
  du_dt = [vx; vy; ax; ay];
end%function

This direct implementation is shorter and better readable than the way via symbolic equations.

You can adapt this for the different constants used, but any change in the constant structure is unphysical, or would need to be justified with some uncommon physical arguments.