《Java数据结构和算法》- 栈和队列
Posted fireway
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了《Java数据结构和算法》- 栈和队列相关的知识,希望对你有一定的参考价值。
Q: 栈、队列与数组的区别?
A: 本篇主要涉及三种数据存储类型:栈、队列和优先级队列,它与数组主要有如下三个区别:
A: (一)程序员工具
数组和其他的结构(栈、队列、链表、树等等)都适用于数据库应用中作为数据记录。它们常用于记录那些对应于现实世界的对象和活动的数据,如职员档案等,这些结构便于数据的访问:它们易于进行插入、删除和查找特定数据项的操作。
然而,本篇要讲解的数据结构和算法更多的是作为程序员的工具来运用。它们主要作为构思算法的辅助工具,而不是完全的数据存储工具。这些数据结构的生命周期比那些数据库类型的结构要短得多。在程序操作执行期间它们才被创建,通常用它们去执行某项特殊的任务;当完成任务之后,它们则被销毁。
A: (二)受限访问
在数组中,若知道数据项的下标,便可以立即访问该数据项;而在本篇的数据结构中,访问是受限制的,即在特定时刻只有一个数据项可以被读取或者删除。
这些结构接口的设计增强了这种受限访问,访问其他数据项理论上是不允许的。
A: (三)更加抽象
栈、队列和优先队列是比数组和其他数据存储结构更为抽象的结构。主要是通过接口对栈、队列和优先队列进行定义,接口表明了它们可以完成的操作,而主要实现机制对用户来说是不可见的。
例如:栈的实现机制可以用数组实现,本篇的示例就是这样处理的,但它也可以用链表来实现。优先级队列的内部实现可以用数组或一种特别的树-堆来实现。
Q: 什么是栈?
A: 栈只允许访问一个数据项:即最后插入的数据项。移除这个数据项才能访问倒数第二个插入的数据项,以此类推。
Q: 栈有哪些实际场景?
A: 大部分微处理器运用基于栈的体系结构,当调用一个方法时,把它的返回值和参数压入栈,当方法结束返回时,哪些数据出栈。栈操作就嵌入在微处理器中。
Q: 栈的Java代码?
A: 在本例中,StackX类里面数据项的类型为long型,是用数组来实现,top变量存储栈顶元素的下标。
示例: StackX.java, StackXTest.java
Q: 栈示例1:单词逆序?
A: 栈的第一个例子是做一件非常简单的事情:单词逆序。因为栈的后进先出(LIFO)的特点,所以字母的顺序就颠倒了。
Q: 栈示例2:分隔符匹配?
A: 栈通常用于匹配左分隔符和右分隔符,因为最后出现的左边分隔符需要最先匹配,这个规律符合栈的LIFO的特点。
下面是一些例子:
c[d] // correct
a{b[c]d}e // correct
a{b(c]d}e // not correct; ] doesn’t match (
a[b{c}d]e} // not correct; nothing matches final }
a{b(c) // not correct; nothing matches opening {
分隔符匹配程序从字符串中不断地读取字符,每次读取一个字符。若发现它是左分隔符,将它压入栈中。当读到一个右分隔符时,弹出栈顶的左分隔符,并且查看它是否和右分隔符向匹配。(注:非分隔符的字符不插入栈中,只需忽略它们。)
Q: 栈的效率?
A: StackX类中实现的栈,入栈和出栈的时间复杂度为常数O(1), 栈操作所消耗的时间不依赖于栈中数据项的个数,因此操作时间很短。栈不需要比较和移动操作。
Q: 什么是队列?
A: 队列(Queue)在词典里是“排队”(waiting line)的意思。计算机科学中,队列是一种数据结构,有点类似栈,只是队列中的第一个插入的数据项最先被移除(先进先出,FIFO),而在栈中,最后插入的数据项最先移除(LIFO)。
Q: 什么是循环队列?
A: 为了避免队列不满却不能插入新数据项的问题,可以让队头队尾指针绕过到数组开始的位置,这就是循环队列。
Q: 队列有哪些实际的场景?
A: 使用文字处理器,敲击一个键,而计算机又暂时要做其他的事情。敲击的内容不会被丢失,它会在队列中等待,知道文字处理程序有时间来读取它。利用队列保证了键入内容在处理时其顺序不会改变。
Q: 队列的Java代码?
A: Queue类不但有mFront(队头)和mRear(队尾),还有队列当中当前数据项的个数mSize。
A: add/offer()方法
将指定的元素插入此队列。区别在于add(e)会抛出异常,offer(e)返回特殊值。
内部调用insert()方法,一般情况,插入操作mRear(队尾指针)加一后,在队尾指针所指的位置处插入新的数据项。但是,当mRear指向数组的最后一个元素,即mItems.length - 1位置的时候,在插入数据项之前,它必须回到数组的第一个元素前面,即mRear设置为-1,因此当mRear加1后,它等于0,是数组第一个元素的下标值。最后,mSize加一。
A: remove()/poll()方法
获取并移除此队列的头。区别在于remove(e)会抛出异常,poll(e)返回特殊值。
内部调用extract()方法,该方法总是由mFront指针得到队头数据项的值,然后将mFront加一。但是,如果这样做mFront会超过数组的大小,mFront必须绕回到数组下标为0的位置上。注意先将返回值临时存储起来。最后mSize减一。
A: peek()方法
获取但不移除此队列的头;如果此队列为空,则返回NULL_ELEMENT。
A: 示例:Queue.java
Q: 没有数据项计数字段的队列Java代码?
A: 在Queue类中包含数据项计数字段mSize会使insert()和extract()方法增加一点额外的操作,因为处理insert()和remove()方法必须分别递增和递减这个变量值。这可能算不上额外的开销,但是如果处理大量的插入和移除操作,这就可能会影响性能。因此,一些队列的实现不使用数据项计数的字段,而是通过mFront和mRear来计算出队列是否为空或者满以及数据项的个数。
示例:Queue.java
Q: 队列的效率?
A: 和栈一样,队列中插入数据项和移除数据项的时间复杂度均为O(1)
Q: 双端队列?
A: 略
Q: 优先级队列?
A: 优先级队列是不同于先进先出队列的另一种队列。每次从队列中取出的是具有最高优先权的元素。
Q: 优先级队列有哪些实际场景?
A: 例如,在抢先式多任务操作系统中,程序排列在优先级队列中,这样优先级最高的程序会得到时间片并得以运行。
Q: 优先级队列的Java代码?
A: 本示例使用有序数组实现优先级队列,这种方式插入比较慢,但是它比较简单,适用于数据量比较小并且不是特别注重插入速度的情况。
A: 最小关键字值得数据项总是数组的高端(最高下标值处),而最大的数据项在低端(下标值为0的位置)。 
A: 待出队的数据项总是在数组的高端,所以删除操作又快又容易。删除数据项后,队头指针下移指向队列新的高端,不需要移动和比较。
A: 注意没有指针回绕,队尾指针从不移动,它总是指着数组低端的元素。
A: Font和Rear指针是为了和普通队列做比较,实际上并不需要它们。
A: 在数据项个数比较少,或不太关心速度的情况下,用数组实现优先级队列还可以满足要求。如果数据项很多,或速度很重要时,采用堆是更好的选择。
Q: 优先级队列的效率?
A: 本示例的优先级队列插入操作需要O(N)时间,而删除操作则需要O(1)的时间。后面将介绍如何通过堆来改进插入操作的时间。
Q: 如何解析算术表达式?
A: 对于诸如 2*(3+4) 或者 ((2+4)*7)+3*(9-5)的算术表达式,前面我们已经演示了怎么应用栈来检查分隔符是否匹配正确,但是接下来我们将学习如何解析这些算术表达式。
事实上,对计算机算法来说如果要直接求算术表达式的值还是相当困难,因此对于算法来说分这两步实现更容易:
1. 将算术表达式转换成另一种形式:后缀表达式
2. 计算后缀表达式的值
Q: 中缀/后缀表达式?
A: 中缀表达式:操作符放在两个操作数之间。比如A+B或A/B等。
A: 后缀表达式:也称作逆波兰表达式(Reverse Polish Notation或者RPN),它是由一位波兰的数学家发明的。操作符跟在两个操作数的后面,而且不包含括号。这样A+B 就变成AB+,A/B变成AB/。
A: 下面是中缀表达式转化为后缀表达式的例子: 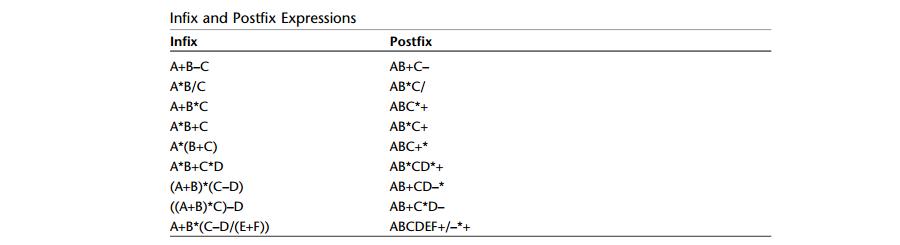
Q: 人类是如何计算中缀表达式?
A: 由于Mr. Klemmer的长期的教学教育,对于3+4+5或者3*(4+5)表达式,我们人类做起这个问题却相当容易。通过分析人类如何计算这些表达式的值,可以得出转化为后缀表达式的启示:
粗略地说,解析算术表达式时,应该遵循下列几条规则:
1. 从左到右读取算式
2. 已经读到了可以计算值得两个操作数和一个操作符时,就可以计算,并用计算结果代替那两个操作数和哪个操作符
3.继续这个过程--从左到右,能算就算--直到表达式的结尾。
A: 示例:3 + 4 - 5


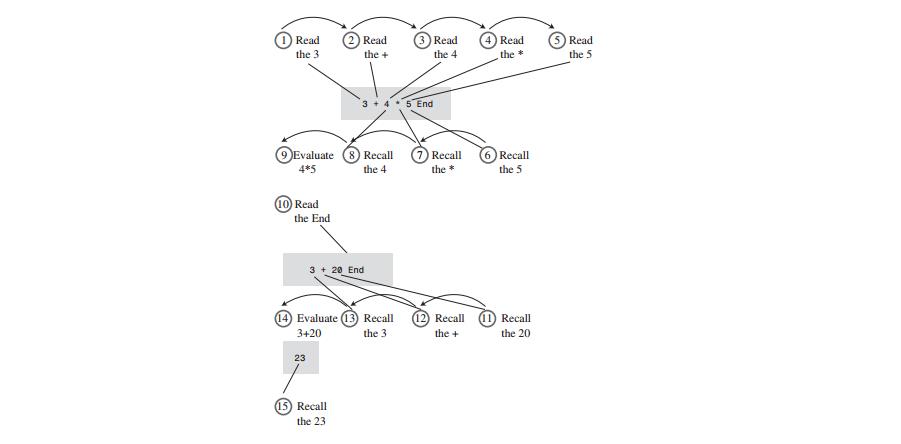
A: 示例: 3 + 4 * 5 
A: 示例: 3 * (4 + 5) 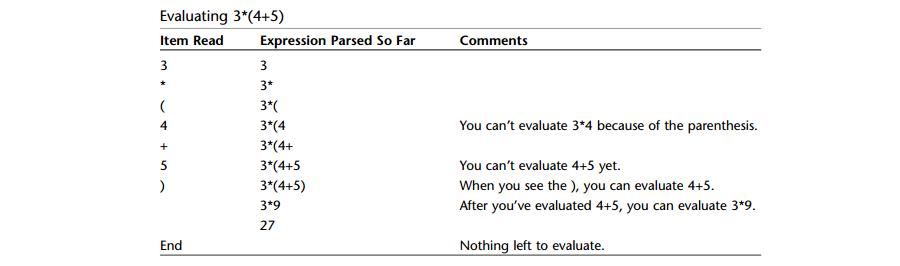

Q: 如何把中缀表达式转换成后缀表达式?
A: 正如前面看到的那样,计算中缀表达式,既要向前,也要向后读表达式。将中缀表达式转换成后缀表达式的规则和计算中缀表达式的规则类似。但是还是有点变化。
A: 将中缀表达式转换成后缀表达式不用做算术运算,它不求中缀表达式的值,只是把操作数和操作符重新排列成另一种形式。
A: 转换规则: 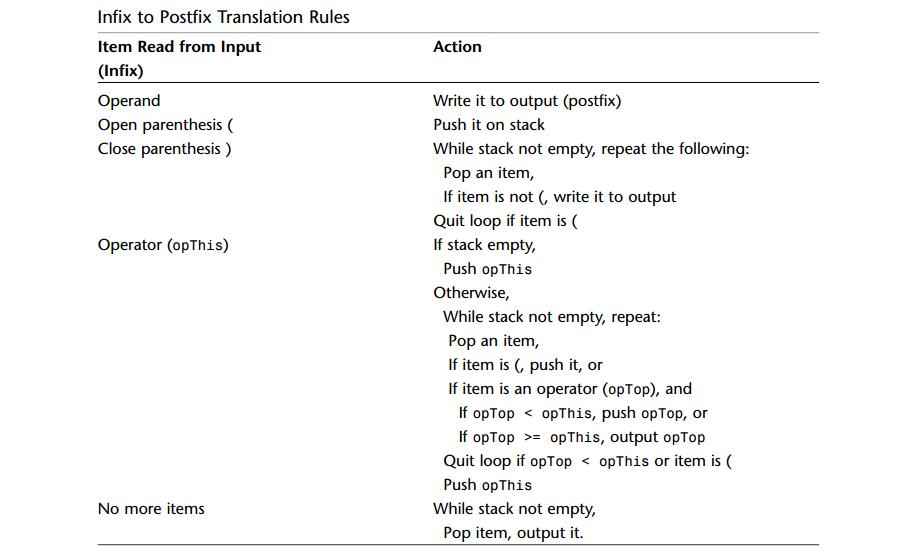
A: 示例:A+B-C 
A: 示例:A+B*C 
A: 示例:A*(B+C) 
Q: 中缀表达式转换成后缀表达式的Java代码 ?
A: 示例: In2PostTransform.java
Q: 人类如何用后缀表达式求值?
A: 下图展示了人类是如何通过观察和铅笔在纸上计算后缀表达式的。
示例:345+*612+/– 
从左边第一个操作符开始,把它和它左边相邻的两个操作数画在一个圆圈里,然后应用操作符运算两个操作数并把结果写在圆圈里。最大的圆圈里算出来的值就是这个表达式最后的结果。
Q: 后缀表达式求值的规则?
A: 怎么才能写一个程序来重复刚才的求值过程呢?正如上面所描述,每遇到一个操作符,就用它来运算在这之前最后看到的两个操作数,这就表明可以利用栈来存储操作数。它的规则如下: 
算术操作的结果被压入到栈中,在最后一个字符(一定是操作符)被读取并执行计算以后,栈里只剩一个数据项,它就是整个表达式的运算结果。
Q: 后缀表达式求值的Java代码?
A: 为了简化代码,这里限制只能输入一位数的数字。
示例:PostfixParser.java
Q: 本篇小结?
- 栈、队列和优先级队列是经常用于简化某些程序操作的数据结构。
- 在这些数据结构中,只有一个数据项可以被访问。
- 栈只允许访问最后一个插入的数据项。
- 队列只允许访问第一个插入的数据项。
- 队列可以实现为循环队列,它基于数组,数组下标可以从数组末端回绕到数组的开始位置。
- 优先级队列的重要操作是有序地插入新数据项和移除关键字最小(有时是最大)的数据项。
- 这些数据结构可以用数组实现,也可以用其他机制(例如链表)来实现。
Q: 参考
- 《Java数据结构和算法》Robert Lafore 著,第4章 - 栈和队列
以上是关于《Java数据结构和算法》- 栈和队列的主要内容,如果未能解决你的问题,请参考以下文章