SVM常考细节

Posted 2023-04-20

参考技术A SVM的原理是什么？

SVM是一种二类分类模型。它的基本模型是在特征空间中寻找间隔最大化的分离超平面的线性分类器。（间隔最大是它有别于感知机）

（1）当训练样本线性可分时，通过硬间隔最大化，学习一个线性分类器，即线性可分支持向量机；

（2）当训练数据近似线性可分时，引入松弛变量，通过软间隔最大化，学习一个线性分类器，即线性支持向量机；

（3）当训练数据线性不可分时，通过使用核技巧及软间隔最大化，学习非线性支持向量机。

注：以上各SVM的数学推导应该熟悉： 硬间隔最大化（几何间隔）---学习的对偶问题---软间隔最大化（引入松弛变量）---非线性支持向量机（核技巧）。

SVM为什么采用间隔最大化？

当训练数据线性可分时，存在无穷个分离超平面可以将两类数据正确分开。

感知机利用误分类最小策略，求得分离超平面，不过此时的解有无穷多个。

线性可分支持向量机 利用间隔最大化求得最优分离超平面 ，这时，解是唯一的。另一方面，此时的分隔超平面所产生的分类结果是 最鲁棒 的，对未知实例的 泛化能力最强 。

然后应该借此阐述，几何间隔，函数间隔，及从函数间隔—>求解最小化1/2 ||w||^2 时的w和b。即线性可分支持向量机学习 算法 —最大间隔法的由来。

为什么要将求解SVM的原始问题转换为其对偶问题？

一、是对偶问题往往更易求解（当我们寻找约束存在时的最优点的时候，约束的存在虽然减小了需要搜寻的范围，但是却使问题变得更加复杂。为了使问题变得易于处理，我们的方法是 把目标函数和约束全部融入一个新的函数，即拉格朗日函数，再通过这个函数来寻找最优点。 ）

二、自然引入核函数，进而推广到非线性分类问题。

为什么SVM要引入核函数？

当样本在原始空间线性不可分时，可将样本从原始空间映射到一个更高维的特征空间，使得样本在这个特征空间内线性可分。

引入映射后的对偶问题：

在学习预测中，只定义核函数 K ( x , y )，而不是显式的定义映射函数 ϕ 。因为 特征空间维数可能很高，甚至可能是无穷维，因此直接计算 ϕ ( x )· ϕ ( y )是比较困难的。 相反，直接计算 K ( x , y )比较容易（即直接在原来的低维空间中进行计算，而不需要显式地写出映射后的结果）。

核函数的定义： K ( x , y )=< ϕ ( x ), ϕ ( y )>，即在特征空间的内积等于它们在原始样本空间中通过核函数K计算的结果。

除了 SVM 之外，任何将计算表示为数据点的内积的方法，都可以使用核方法进行非线性扩展。

svm RBF核函数的具体公式？

Gauss径向基函数则是局部性强的核函数，其外推能力随着参数σ的增大而减弱。

这个核会将原始空间映射为无穷维空间。不过，如果 σ 选得很大的话，高次特征上的权重实际上衰减得非常快，所以实际上（数值上近似一下）相当于一个低维的子空间；反过来，如果 σ 选得很小，则可以将任意的数据映射为线性可分——当然，这并不一定是好事，因为随之而来的可能是非常严重的过拟合问题。不过，总的来说，通过调控参数 σ ， 高斯核实际上具有相当高的灵活性，也是使用最广泛的核函数之一。

为什么SVM对缺失数据敏感？

这里说的缺失数据是指缺失某些特征数据，向量数据不完整。SVM没有处理缺失值的策略（决策树有）。而SVM希望样本在特征空间中线性可分，所以特征空间的好坏对SVM的性能很重要。缺失特征数据将影响训练结果的好坏。

SVM是用的是哪个库？Sklearn/libsvm中的SVM都有什么参数可以调节？

用的是sklearn实现的。采用sklearn.svm.SVC设置的参数。本身这个函数也是基于libsvm实现的（PS: libsvm中的二次规划问题的解决算法是SMO）。

SVC函数的训练时间是随训练样本平方级增长，所以不适合超过10000的样本。

对于多分类问题，SVC采用的是one-vs-one投票机制，需要两两类别建立分类器，训练时间可能比较长。

sklearn.svm.SVC( C=1.0 , kernel='rbf' , degree=3 , gamma='auto' , coef0=0.0 , shrinking=True , probability=False , tol=0.001 , cache_size=200 , class_weight=None , verbose=False , max_iter=-1 , decision_function_shape=None , random_state=None )

参数：

l  C：C-SVC的惩罚参数C?默认值是1.0

C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集 测试 时准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。

l kernel ：核函数，默认是rbf，可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’

0 – 线性：u'v

1 – 多项式：(gamma*u'*v + coef0)^degree

2 – RBF函数：exp(-gamma|u-v|^2)

3 –sigmoid：tanh(gamma*u'*v + coef0)

l degree ：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略。

l gamma ： ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’，则会选择1/n_features

l coef0 ：核函数的常数项。对于‘poly’和 ‘sigmoid’有用。

l probability： 是否采用概率估计？.默认为False

l shrinking ：是否采用shrinking heuristic方法，默认为true

l tol： 停止训练的误差值大小，默认为1e-3

l cache_size ：核函数cache缓存大小，默认为200

l class_weight ：类别的权重，字典形式传递。设置第几类的参数C为weight*C(C-SVC中的C)

l verbose ：允许冗余输出？

l max_iter ：最大迭代次数。-1为无限制。

l decision_function_shape ：‘ovo’, ‘ovr’ or None, default=None3

l random_state ：数据洗牌时的种子值，int值

主要调节的参数有：C、kernel、degree、gamma、coef0。

SVM如何处理多分类问题？

一般有两种做法：一种是直接法，直接在目标函数上修改，将多个分类面的参数求解合并到一个最优化问题里面。看似简单但是计算量却非常的大。

另外一种做法是间接法：对训练器进行组合。其中比较典型的有 一对一 ，和 一对多 。

一对多，就是对每个类都训练出一个分类器，由svm是二分类，所以将此而分类器的两类设定为目标类为一类，其余类为另外一类。这样针对k个类可以训练出k个分类器，当有一个新的样本来的时候，用这k个分类器来测试，那个分类器的概率高，那么这个样本就属于哪一类。这种方法效果不太好，bias比较高。

svm一对一法（one-vs-one），针对任意两个类训练出一个分类器，如果有k类，一共训练出C(2,k) 个分类器，这样当有一个新的样本要来的时候，用这C(2,k) 个分类器来测试，每当被判定属于某一类的时候，该类就加一，最后票数最多的类别被认定为该样本的类。

干货 | 详解支持向量机（附学习资源）

选自The Yhat 

机器之心编译

参与：Jane W、蒋思源

支持向量机（SVM）已经成为一种非常流行的算法。本文将尝试解释支持向量机的原理，并列举几个使用 Python Scikits 库的例子。本文的所有代码已经上传 Github。有关使用 Scikits 和 Sklearn 的细节，我将在另一篇文章中详细介绍。

什么是 支持向量机（SVM）？

SVM 是一种有监督的机器学习算法，可用于分类或回归问题。它使用一种称为核函数（kernel）的技术来变换数据，然后基于这种变换，算法找到预测可能的两种分类之间的最佳边界（optimal boundary）。简单地说，它做了一些非常复杂的数据变换，然后根据定义的标签找出区分数据的方法。

为什么这种算法很强大？

在上面我们说 SVM 能够做分类和回归。在这篇文章中，我将重点讲述如何使用 SVM 进行分类。特别的是，本文的例子使用了非线性 SVM 或非线性核函数的 SVM。非线性 SVM 意味着算法计算的边界不再是直线。它的优点是可以捕获数据之间更复杂的关系，而无需人为地进行困难的数据转换；缺点是训练时间长得多，因为它的计算量更大。

牛和狼的分类问题

什么是核函数技术？

核函数技术可以变换数据。它具备一些好用的分类器的特点，然后输出一些你无需再进行识别的数据。它的工作方式有点像解开一条 DNA 链。从传入数据向量开始，通过核函数，它解开并组合数据，直到形成更大且无法通过电子表格查看的数据集。该算法的神奇之处在于，在扩展数据集的过程中，能发现类与类之间更明显的边界，使得 SVM 算法能够计算更为优化的超平面。

现在假装你是一个农夫，那么你就有一个问题——需要建立一个篱笆，以保护你的牛不被狼攻击。但是在哪里筑篱笆合适呢？如果你真的是一个用数据说话的农夫，一种方法是基于牛和狼在你的牧场的位置，建立一个分类器。通过对下图中几种不同类型的分类器进行比较，我们看到 SVM 能很好地区分牛群和狼群。我认为这些图很好地说明了使用非线性分类器的好处，可以看到逻辑回归和决策树模型的分类边界都是直线。

重现分析过程

想自己绘出这些图吗？你可以在你的终端或你选择的 IDE 中运行代码，在这里我建议使用 Rodeo（Python 数据科学专用 IDE 项目）。它有弹出制图的功能，可以很方便地进行这种类型的分析。它也附带了针对 Windows 操作系统的 Python 内核。此外，感谢 TakenPilot（一位编程者 https://github.com/TakenPilot）的辛勤工作，使得 Rodeo 现在运行闪电般快速。

下载 Rodeo 之后，从我的 github 页面中下载 cows_and_wolves.txt 原始数据文件。并确保将你的工作目录设置为保存文件的位置。

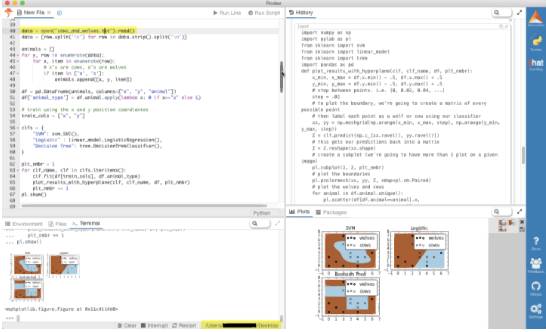
好了，现在只需将下面的代码复制并粘贴到 Rodeo 中，然后运行每行代码或整个脚本。不要忘了，你可以弹出绘图选项卡、移动或调整它们的大小。

# Data driven farmer goes to the Rodeoimport numpy as npimport pylab as plfrom sklearn import svmfrom sklearn import linear_modelfrom sklearn import treeimport pandas as pddef plot_results_with_hyperplane(clf, clf_name, df, plt_nmbr):    x_min, x_max = df.x.min() - .5, df.x.max() + .5    y_min, y_max = df.y.min() - .5, df.y.max() + .5    # step between points. i.e. [0, 0.02, 0.04, ...]    step = .02    # to plot the boundary, we're going to create a matrix of every possible point    # then label each point as a wolf or cow using our classifier    xx, yy = np.meshgrid(np.arange(x_min, x_max, step), np.arange(y_min, y_max, step))    Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])    # this gets our predictions back into a matrix    Z = Z.reshape(xx.shape)    # create a subplot (we're going to have more than 1 plot on a given image)    pl.subplot(2, 2, plt_nmbr)    # plot the boundaries    pl.pcolormesh(xx, yy, Z, cmap=pl.cm.Paired)    # plot the wolves and cows    for animal in df.animal.unique():        pl.scatter(df[df.animal==animal].x,                   df[df.animal==animal].y,                   marker=animal,                   label="cows" if animal=="x" else "wolves",                   color='black')    pl.title(clf_name)    pl.legend(loc="best")data = open("cows_and_wolves.txt").read()data = [row.split('\t') for row in data.strip().split('\n')]animals = []for y, row in enumerate(data):    for x, item in enumerate(row):        # x's are cows, o's are wolves        if item in ['o', 'x']:            animals.append([x, y, item])df = pd.DataFrame(animals, columns=["x", "y", "animal"])df['animal_type'] = df.animal.apply(lambda x: 0 if x=="x" else 1)# train using the x and y position coordiantestrain_cols = ["x", "y"]clfs = {    "SVM": svm.SVC(),    "Logistic" : linear_model.LogisticRegression(),    "Decision Tree": tree.DecisionTreeClassifier(),}plt_nmbr = 1for clf_name, clf in clfs.iteritems():    clf.fit(df[train_cols], df.animal_type)    plot_results_with_hyperplane(clf, clf_name, df, plt_nmbr)    plt_nmbr += 1pl.show()

SVM 解决难题

在因变量和自变量之间的关系是非线性的情况下，带有核函数的 SVM 算法会得到更精确的结果。在这里，转换变量（log(x),(x ^ 2)）就变得不那么重要了，因为算法内在地包含了转换变量的过程。如果你思考这个过程仍然有些不清楚，那么看看下面的例子能否让你更清楚地理解。

假设我们有一个由绿色和红色点组成的数据集。当根据它们的坐标绘制散点图时，点形成具有绿色轮廓的红色圆形（看起来很像孟加拉国的旗子）。

如果我们丢失了 1/3 的数据，那么会发生什么？如果无法恢复这些数据，我们需要找到一种方法来估计丢失的 1/3 数据。

那么，我们如何弄清缺失的 1/3 数据看起来像什么？一种方法是使用我们所拥有的 80％数据作为训练集来构建模型。但是使用什么模型呢？让我们试试下面的模型：

• 逻辑回归模型

• 决策树

• 支持向量机

对每个模型进行训练，然后用这些模型来预测丢失的 1/3 数据。下面是每个模型的预测结果：

模型算法比较的实现

下面是比较 logistic 模型、决策树和 SVM 的代码。

import numpy as npimport pylab as plimport pandas as pdfrom sklearn import svmfrom sklearn import linear_modelfrom sklearn import treefrom sklearn.metrics import confusion_matrix x_min, x_max = 0, 15y_min, y_max = 0, 10step = .1# to plot the boundary, we're going to create a matrix of every possible point# then label each point as a wolf or cow using our classifierxx, yy = np.meshgrid(np.arange(x_min, x_max, step), np.arange(y_min, y_max, step))df = pd.DataFrame(data={'x': xx.ravel(), 'y': yy.ravel()})df['color_gauge'] = (df.x-7.5)**2 + (df.y-5)**2df['color'] = df.color_gauge.apply(lambda x: "red" if x <= 15 else "green")df['color_as_int'] = df.color.apply(lambda x: 0 if x=="red" else 1)print "Points on flag:"print df.groupby('color').size()printfigure = 1# plot a figure for the entire datasetfor color in df.color.unique():    idx = df.color==color    pl.subplot(2, 2, figure)    pl.scatter(df[idx].x, df[idx].y, color=color)    pl.title('Actual')train_idx = df.x < 10train = df[train_idx]test = df[-train_idx]print "Training Set Size: %d" % len(train)print "Test Set Size: %d" % len(test)# train using the x and y position coordiantescols = ["x", "y"]clfs = {    "SVM": svm.SVC(degree=0.5),    "Logistic" : linear_model.LogisticRegression(),    "Decision Tree": tree.DecisionTreeClassifier()}# racehorse different classifiers and plot the resultsfor clf_name, clf in clfs.iteritems():    figure += 1    # train the classifier    clf.fit(train[cols], train.color_as_int)    # get the predicted values from the test set    test['predicted_color_as_int'] = clf.predict(test[cols])    test['pred_color'] = test.predicted_color_as_int.apply(lambda x: "red" if x==0 else "green")    # create a new subplot on the plot    pl.subplot(2, 2, figure)    # plot each predicted color    for color in test.pred_color.unique():        # plot only rows where pred_color is equal to color        idx = test.pred_color==color        pl.scatter(test[idx].x, test[idx].y, color=color)    # plot the training set as well    for color in train.color.unique():        idx = train.color==color        pl.scatter(train[idx].x, train[idx].y, color=color)    # add a dotted line to show the boundary between the training and test set    # (everything to the right of the line is in the test set)    #this plots a vertical line    train_line_y = np.linspace(y_min, y_max) #evenly spaced array from 0 to 10    train_line_x = np.repeat(10, len(train_line_y)) #repeat 10 (threshold for traininset) n times    # add a black, dotted line to the subplot    pl.plot(train_line_x, train_line_y, 'k--', color="black")    pl.title(clf_name)    print "Confusion Matrix for %s:" % clf_name    print confusion_matrix(test.color, test.pred_color)pl.show()

在 Rodeo 中复制和运行上面的代码。

结果

从这些图中可以清楚地看出 SVM 更好。为什么呢？如果观察决策树和 GLM（广义线性模型，这里指 logistic 回归）模型的预测形状，你会看到预测给出的直边界。因为它们的输入模型没有任何变换来解释 x、y 以及颜色之间的非线性关系。给定一组特定的变换，我们绝对可以使 GLM 和 DT（决策树）得出更好的结果，但寻找合适的变换将浪费大量时间。在没有复杂的变换或特征缩放的情况下，SVM 算法 5000 数据点只错误地分类了 117 点（98％的精度，而 DT 精确度为 51％，GLM 精确度为 12％）。由于所有错误分类的点是红色，所以预测的结果形状有轻微的凸起。

不适用的场合

那为什么不是所有问题都使用 SVM？很遗憾，SVM 的魅力也是它最大的缺点。复杂数据变换以及得到的决策边界平面是很难解释的。这就是为什么它通常被称为「黑箱」的原因。GLM 和决策树恰恰相反，它们的算法实现过程及怎样减少成本函数得到优良结果都很容易理解。

更多学习资源

想了解更多关于 SVM 的知识？以下是我收藏的一些好资源：

初级——SVM 教程：基础教程，作者是 MIT 的 Zoya Gavrilov

初级——SVM 算法原理：Youtube 视频，作者是 Thales SehnKörting

中级——支持向量机在生物医学中的简要介绍：纽约大学 & 范德堡大学提供的课件

高级——模式识别下的支持向量机教程：作者是贝尔实验室（Bell Labs）的 Christopher Burges

原文链接：http://blog.yhat.com/posts/why-support-vector-machine.html

✄------------------------------------------------

加入机器之心（全职记者/实习生）：[e-mail]

投稿或寻求报道：[e-mail]

广告&商务合作：[e-mail]