《Python神经网络》3——神经网络矩阵乘法

Posted 2023-04-20

参考技术A 按照以下图示，最终的神经网络调参，以最简单的3层神经网络为例，公式如下：

        怎么求这个函数的最优解？

如果不试图耍聪明，那么我们可以只是简单地尝试随机组合权重，直到找到好的权重组合。

当陷入一个困难的问题而焦头烂额时，这不算是一个疯狂的想法。这种方法一般称为暴力方法。

暴力方法的不好之处：

假设每个权重在-1和+1之间有1000种可能的值。那么对于3层、每层3个节点的神经网络，可以得到18个权重，因此有18000种可能性需要测试。如果一个相对经典的神经网络，每层有500个节点，那么需要测试5亿种权重的可能性。如果每组组合需要花费1秒钟计算，那么对于一个训练样本，就需要花费16年更新权重！对于1000种训练样本，要花费16000年！       这就是暴力方法不切实际之处。

数学家多年来也未解决这个难题，直到20世纪60年代到70年代，这个难题才有了切实可行的求解办法。

如何解决这样一个明显的难题呢？——我们必须做的第一件事是，拥抱悲观主义。

Python实现矩阵乘法

​

问题

矩阵相信大家都知道，是线性代数中的知识，就是一系列数集。顾名思义，数字组成的矩形，例如：

[1 2 3 4

5 67 8

9 1011 ]

现在，我们需要用python编程来实现矩阵的乘法。

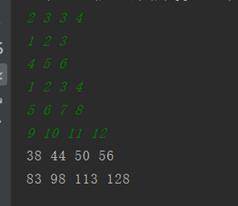
输入示例：

2 3 3 4

1 2 3

4 5 6

1 2 3 4

5 6 7 8

9 10 11 12

输出示例：

38 44 50 56

83 98 113 128

注意：输入的第一行分别为两个矩阵的行列数（表示为：N1，M1，N2，M2）。

方法

矩阵乘法原理

要做矩阵的乘法，首先得搞清楚几点关于矩阵乘法的知识。

只有一个矩阵的列数等于另一个矩阵的行数时，这两个矩阵才能相乘。

矩阵乘法的原理是，一个矩阵的每一行分别与另一个矩阵的每一列的每一个数一一对应相乘再相加，得到的数字就是结果矩阵的中的一个数。

结果矩阵的形状是一个矩阵的行数和另一个矩阵的列数。如A23 * B34 =C2*4.总结出来就是：‘中间相等，取两头’。

Python实现矩阵乘法

知道了矩阵乘法的原理后，再一起来看看如何用python编写出程序吧。如何输入输出矩阵就不说了，直接看中间的算法。有以下几个步骤：

“定循环”。先根据乘法的原理，得出结果矩阵的形状，比如：A23 * B34 =C24，结果矩阵为2行4列，所以就一共有24个数字，也就是说程序需要循环24次。则循环可定为N1M2.

“定因数”。每一次相乘时，两个因数都会改变，所以需要在循环开始出设置变量，这样每一次的变量都会更新。

“定结果”。在每一次循环时，需要算出一个结果，为了计算简便，可使用匿名函数lambda，其用法为lambdax:function,iterable.其中x为iterable的遍历。分别执行function。

代码示例

lis1,lis2 = [],[]

N1,M1,N2,M2 = map(int,input().split())

for i in range(N1):

     nums = list(map(int,input().split()))

     lis1.append(nums)

for i in range(N2):

     nums = list(map(int,input().split()))

     lis2.append(nums)

res = []

for a in range(N1):

     res.append([])

     for b in range(M2):

         lis4 = []

         lis3 = lis1[a]

         for c in range(N2):

            lis4.append(lis2[c][b])

         res_num = sum(map(lambda x,y:x*y,lis3,lis4))

         res[a].append(res_num)

for i in res:

     for o in i:

         print(o,end=' ')

     print()

运行效果

结语

Python中很多东西常常与数学有关，要想做正确，还得究其原理。对于矩阵乘法，可以是说得非常详细了，甚至会显得有点啰嗦，但是，所体现的是对于一个问题的解题思路。关键在于解题的方法，是需要一步一步来看的。这才是本文所要告诉大家的。

​