python进阶-- numpy基本功能

Posted 2023-02-18 文仙草

Numpy是用于科学计算的python包。

一、创建numpy数组(array)

A numpy array or ND array 与python数据结构中的列表(list)非常相似，不过numpy array一般大小固定，且其中每个元素的类型相同，比如都是整数型、都是浮点型。

创建numpy array时，需要先import numpy。numpy array的数据类型是numpy.ndarray.（不是list哦！）

（一）创建一维数组(array)

import numpy as np
a = np.array([0,1,2,3,4])
type(a)
#numpy.ndarray
a.dtype
#dtype('int32')

如果array里有一个元素是文字，则所有元素都会变成文字类型

一些常用的查询array属性的方法：

• a.dtype： 返回array的数据类型
• a.size：返回array中元素的个数
• a.shape：返回每个维度下的元素个数，元组(tuple)形式
• a.ndim：返回array的维度，一维数组为1，二维数组为2， n维数组为n

a = np.array([0,1,2,3,4])
a.dtype  # dtype('int32')
a.size   # 5
a.shape  # (5,)
a.ndim   # 1

（二）创建多维数组(array)

#二维数组
a = [[1,2,3],[4,5,6],[7,8,9]]
A = np.array(a)
# A =  ｜1,2,3｜
#      ｜4,5,6｜
#      ｜7,8,9｜
#A是一个二维数组。
A.ndim
# 2 
# 可以认为A.ndim表示有多少层括号
A.shape
#(3,3)
#A.shape反应了每层括号里所包含的元素个数，即每个维度下的元素个数。
#比如A有3行（第一层括号有3个元素）和3列（每个第二层括号里都有3个元素）
A.size
# 9
# A.size返回整个数组的元素个数，比如A中一共有3*3=9个元素。

二、index and slice

（一）一维数组index和slicing

1. Index和修改数据

2. Slicing和修改数据

利用切片一次性修改多个数据的时候，新数据赋值时不用加方括号！

3. 用列表list选择和修改array中元素的值

下图中列表select给出了从array选择的元素的index，c是被选择的array, d是选择后的array

（二）二维数组（矩阵）index和slicing

1. Index

矩阵名[行数，列数] 或者 矩阵名[行数][列数]

#获取下图矩阵A的第二行、第三列数据
#注意行、列均从0开始编号
A[1,2]
#结果: 23
A[1][2]
#结果：23

#获取下图矩阵A的第一行、第一列数据
#注意行、列均从0开始编号
A[0][0]
#结果: 11

2. Slicing

矩阵名[行数范围，列数范围] 或者 矩阵名[行数范围][列数范围]
返回值是array结构

#获取矩阵A的第1行、第1-2列的数据
A[0][0:2]
#结果
#array([11, 12])

#获取矩阵A的第1-2行、第3列的数据
A[0:2][2]
#结果
#array([13, 23])

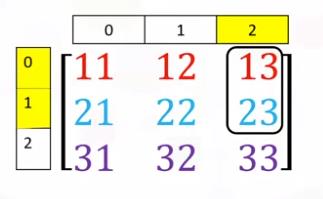
注意：A[0:2][0:2] 与A[0:2,0:2]获取的数据区别

A[0:2,0:2]
#结果
#array([[11, 12],
#       [21, 22]])
#获取矩阵A的第1-2行、第1-2列的数据

A[0:2][0:2]
#结果
#array([[11, 12, 13],
#       [21, 22, 23]])
#相当于先获取矩阵A的第1-2行数据（矩阵A_1），再获取A'的第1-2行数据，即
#A_1 = A[0:2]
#A[0:2][0:2] = A_1[0:2]

如果想获取矩阵A第1-2列数据的第2-3行数据：

#最直接
A[1:3,0:2]
#结果
#array([[21, 22],
#       [31, 32]])


#如果想行列拆开写，先获取第2-3行全部数据，然后从中获取第1-2列的数据
A[1:3][:,0:2]
#结果
#array([[21, 22],
#       [31, 32]])


#或者，先获取第1-2列全部数据，然后从中获取第2-3行的数据
A[:,0:2][1:3]
#结果
#array([[21, 22],
#       [31, 32]])

三、基础算法 - 一维数组（向量）

(一）向量(vector)加减

不使用numpy的时候，需要用loop将每对元素相加

#将两个向量u和v相加，不使用numpy
u = [0,1]
v = [1,3]
z = []
for n, m in zip(u,v):
    z.append(n+m)
#【结果】
# z = [1,4]

如果使用numpy，计算速度会更快

#将两个向量u和v相加，使用numpy
import numpy as np
u = np.array([0,1])
v = np.array([1,3])
z = u+v
#【结果】
# z = [1,4]

也可以进行向量减法、向量与常数相乘、向量与常数相加

z = u-v
#【结果】
# z = [-1,-2]

z1 = z*2
#【结果】
# z = [-2,-4]

z2 = z + 2
#【结果】
# z = [1,0]

还可以进行向量乘法（结果为一个向量）、向量点积（结果为一个数值）

u = [1,2]
v = [3,4]
z = u*v
#【结果】
# z = [1*3+1*4,2*3+2*4] = [7,14]

z1 = np.dot(u,v)
#【结果】
# z1 = 1*3+2*4 = 11

需要注意，向量乘法不满足交换律，即u * v != v * u

z2 = v*u
#【结果】
# z2 = [3*1+3*2,4*1+4*2] = [9,12]

四、通用功能 - 一维数组

• 最小值、最大值、标准差、平均值等，min(), max(), std(), mean()

a = np.array([1,-2,3,4])
#求平均
mean_a = a.mean()
# mean_a = (1-2+3+4)/4 = 1.5
#找最大值
max_a = a.max()
#max_a = 4
min_a = a.min()
#min_a = -2
std_a = a.std()
#std_a = 2.29128784747792

• np.pi & .sin()

# np.pi是圆周率，求sin()
x = np.array([0, np.pi/2, np.pi])
y = np.sin(x)
#y = [sin(0), sin(np.pi/2), sin(np.pi)] = [0, 1, 0]

• np.linespace(start point, end point, 元素个数)：创建均匀分布的数列

x = np.linespace(-2, 2, num = 5)
#x = [-2, -1, 0, 1, 2]

y = np.linespace(-2, 2, num = 9)
#y = [-2, -1.5, -1, -0.5, 0, 0.5, 1, 1.5, 2]

五、基础算法–二维数组（矩阵）

1. 矩阵加法、与常量相乘、Hadamard乘积（按元素相乘）

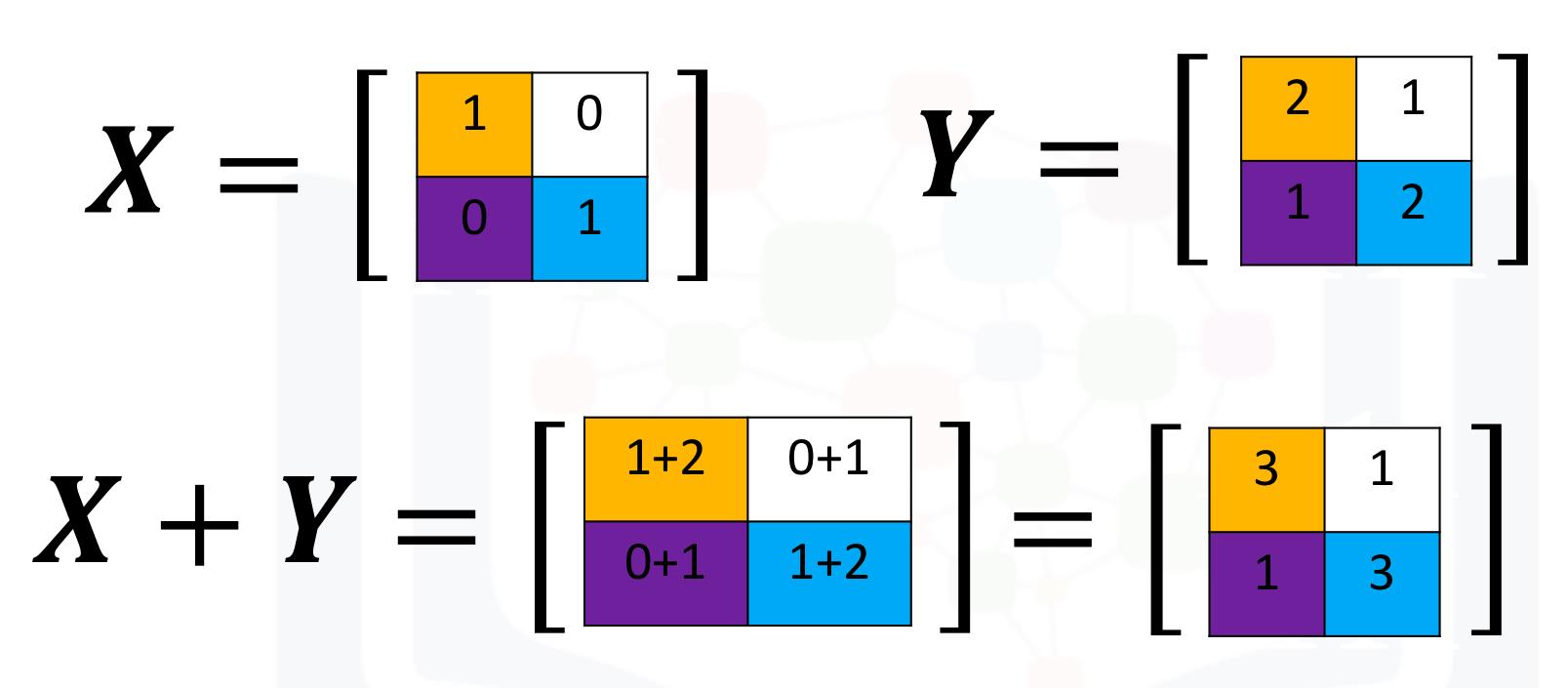
• 矩阵加法

x = np.array([[1,0],[0,1]])
y = np.array([[2,1],[1,2]])

z = x+y
# z: array([[3,1],[1,3]])

• 矩阵与常数相乘

z1 = 2*y
# z1: array([[4,2],[2,4]])

• 矩阵Hadamard乘积（即矩阵各元素相乘）

z2 = x*y
#z2: array([[1*2,0*1],[0*1,1*2]]) = array([[2,0],[0,2]])

2. 矩阵乘法

x = np.array([[0,1,1],[1,0,1]])
y = np.array([[1,1],[1,1],[-1,1]])
#矩阵乘法的时候，需要保证前面矩阵的行数与后面矩阵的列数相等。
z = np.dot(x,y)
# z: array([[0*1+1*1+1*-1,0*1+1*1+1*1],[1*1+0*1+1*-1,1*1+0*1+1*1]]) ---> array([[0,2],[0,2]])

3. 矩阵转置

C = np.array([[1,1],[2,2],[3,3]])
C
#array([[1, 1],
#       [2, 2],
#       [3, 3]])
C.T
#array([[1, 2, 3],
#       [1, 2, 3]])

4. 其他

• np.sin() : 对矩阵中各个元素分别求sin值

Z = np.array([[0,2],[0,2]])
np.sin(Z)

#结果
#array([[0.        , 0.90929743],
#       [0.        , 0.90929743]])