用改进的欧拉公式求初值问题！如能解答，万分感谢！

Posted 2023-04-17

参考技术A

Author：Wacs5

Date：20090106(YYYY-MM-DD)

Function：欧拉方法与改进的欧拉方法求常微分方程

Describe

用欧拉方法与改进的欧拉方法求初值问题dy/dx=(2x)/(3y^2)

y(0)=1 ，在区间[0，1]上取步长h=0.1的数值解。

要求：显示各x值下(0、0.1、0.2… 0.9、1)两种方法计算的y值。

扩展资料：

可以将区间[a,b]分成n段，那么方程在第xi点有y'(xi)=f(xi,y(xi))，再用向前差商近似代替导数则为：(y(xi+1)-y(xi))/h= f(xi,y(xi))，在这里，h是步长，即相邻两个结点间的距离。因此可以根据xi点和yi点的数值计算出yi+1来：

yi+1= yi+h*f(xi ,yi)，i=0,1,2,L

这就是欧拉公式，若初值yi+1是已知的，则可依据上式逐步算出数值解y1,y2,L。

参考资料来源：百度百科-改进欧拉法

euler公式

参考技术A

欧拉公式（英语：Euler's formula，又称尤拉公式）是复分析领域的公式，它将三角函数与复指数函数关联起来，因其提出者莱昂哈德·欧拉而得名。

复变函数中，e^(ix)=(cos x+isin x)称为欧拉公式，e是自然对数的底，i是虚数单位。

拓扑学中，在任何一个规则球面地图上，用 R记区域个 数 ，V记顶点个数 ，E记边界个数 ，则 R+ V- E= 2，这就是欧拉定理 ，它于 1640年由 Descartes首先给出证明。

后来 Euler(欧拉 )于 1752年又独立地给出证明 ，我们称其为欧拉定理 ，在国外也有人称其 为 Descartes定理。

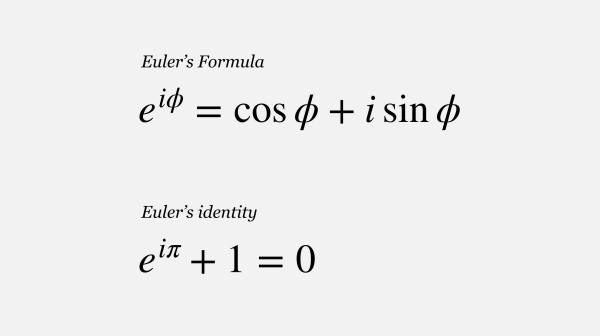
复数幂的定义

指数函数Ë X为的实际值X可以在几个不同的等效的方式来定义（见指数函数的表征）。

这些中的一些方法可以直接延伸到给的定义Ë ž为复数值ž简单地通过取代ž代替X和使用复杂的代数运算。

特别是我们可以使用以下三个定义中的任何一个，它们是等效的。