12. 批标准化（Batch Normalization ）

Posted 2023-04-15

参考技术A

Batch Normalization算法自从15年提出，到现在已经成为深度学习中经常使用的技术，可以说是十分powerful。

我们先从Feature Scaling或者Feature Normalization说起，不管你是不是做深度学习的方法，其实你都会想要做Feature Scaling。原因是：

在没有进行Feature Scaling之前，如果两个输入数据 的distribution很不均匀的话，导致 对计算结果的影响比较大（图左），所以训练的时候，横纵方向上需要给与一个不同的training rate，在 方向需要一个更大的learning rate， 方向给与一个较小的learning rate，不过这样做的办法却不见得很简单。所以对不同Feature做了normalization之后，使得error surface看起来比较接近正圆的话（图右），就可以使训练容易得多。

不管你是不是deep learning的方法，你都会用到Feature Scaling技术。通常 经典的Feature Scaling 的方法是怎么做的？

现在给你一大堆的数据，你的训练数据总共有大 笔data。而接下来你就对每一个dimension去计算dimension的 mean 跟dimension的 standard deviation ，假设你这个input是39维，所以就算出39个mean跟39个standard deviation；然后对每一维中的数值，假设你取第 维中的数值出来，你就把它 减掉第 维的mean，除以第 维的standard deviation，作为一个Normalization ，你就会让第 维的feature的分布 mean=0，variance=1 ，一般来说，如果你今天做了Feature Scaling这件事情往往会让你的training变得比较快速。

刚才都是还没有讲到deep learning了，现在我们进入deep learning的部分，我们知道说在deep learning里面它的卖点就是有很多个layer，你有个 进来通过一个layer得到 ，把 放入layer 2得到输出 ，我们当然会对network输入的 做Feature Scaling。但是你仔细想想从layer 2的角度来看，其实它的input的feature是 ，我们可以把network前几个layer想成是一个feature的提取，我们知道说network的前几个layer的工作其实就是在抽比较好的feature，后面几个layer当做classify可以做得更好，所以对layer 2来说，他吃到的feature就是layer 1的output ，如果我们觉得说Feature Scaling是有帮助的，我们也应该对layer 2 的feature，也就是layer 1的output 做Feature Scaling，同理layer 2的输出 他是下一个Layer 3的输入，它是下一个layer的feature，我们应该要做一下Normalization，这样接下来layer可以learn的更好。

其实对每一个layer做Normalization这件事情，在deep learning上面是很有帮助的，因为它解决了一个叫做 Internal Covariate Shift 的这个问题，可以令这个问题比较轻微一点。

Internal Covariate Shift 这个问题是什么意思？
如上图所示：你就想成说现在每一个人代表1个layer，然后他们中间是用话筒连在一起，而今天当一个人手上的两边的话筒被接在一起的时候，整个network的传输才会顺利，才会得到好的performance。

现在我们看一下中间那个小人，他左手边的话筒比较高，他的右手边的话筒比较低。在训练的时候为了将两个话筒拉到同一个水平高度，它会将左手边的话筒放低一点，同时右手的话筒放高一点，因为是同时两边都变，所以就可能出现了下面的图，最后还是没对上。

在过去的解决方法是调小learning rate，因为没对上就是因为学习率太大导致的，虽然体调小learning rate可以很好地解决这个问题，但是又会导致训练速度变得很慢。

你不想要学习率设小一点，所以怎么办？

所以今天我们要讲batch Normalization，也就是对每一个layer做Feature Scaling这件事情，就可以来处理Internal Covariate Shift问题。
为什么？因为如果我们今天把每一个layer的feature都做Normalization，我们把每一个layer的feature的output都做Normalization，让他们永远都是比如说 ，对下一个layer来看，前个layer的statistics就会是固定的，他的training可能就会更容易一点。

首先我们把刚才的话筒转化为deep learning中就是说，训练过程参数在调整的时候前一个层是后一个层的输入，当前一个层的参数改变之后也会改变后一层的参数。当后面的参数按照前面的参数学好了之后前面的layer就变了，因为前面的layer也是不断在变的。其实输入数据很好normalization，因为输入数据是固定下来的，但是后面层的参数在不断变化根本就不能那么容易算出mean和variance，所以需要一个新的技术叫Batch normalization。

Batch的数据其实是平行计算的，如下图。实际上gpu在运作的时候，它会把 拼在一起，排在一起变成一个matrix，把这个matrix乘上 得到 ，因为今天是matrix对matrix，你如果把matrix对matrix作平行运算，可以比matrix对三个data分开来进行运算速度还要快，这个就是gpu加速batch运算的原理。

接下来我们要做 Batch Normalization 。怎么做？我们现在想要做的事情是对第一个隐藏层的output， ，做Normalization。

我们可以先做Normalization，再通过激活函数，或者先通过激活函数再做Normalization。我们偏向于先做Normalization，再通过激活函数，这样做有什么好处呢？
因为你的激活函数，如果你用tanh或者是sigmoid，函数图像的两端，相对于 的变化， 的变化都很小。也就是说，容易出现梯度衰减的问题。因此你比较喜欢你的input是落在变化比较大的地方，也就是你的前后 零 的附近，如果先做Normalization你就能够确保说在进入激活函数之前，你的值是落在你的附近。

我们现在来做Normalization：你想要先算出一个 ， ，先算出这些 的均值。接下来算一下 ， 。好，接下来这边有件事情要跟大家强调一下，就是 是是由 决定的。 是由 和 决定的。等一下会用上。

这边有一件事情要注意:在做Normalization的话，在选的 跟 的时候我们其实希望它代表的是 整个training set全体的statistics 。但是因为实做上统计整个training set全体的statistics是非常耗费时间的，而且不要忘了 的数值是不断的在改变的，你不能说我把整个training set的data导出来算个 ，然后 的数值改变以后，再把整个导出来的再算一次 ，这个是不切实际的做法;
所以现在我们在算 跟 的时候，只会在batch里面算，这意味着什么？ 这意味着说你的batch size一定要够大 ，如果太小的话Batch Normalization的性能就会很差，因为你没有办法从一个batch里面估测整个data的 跟 ，举例来说，你可以想象极端case，如果今天batch size=1，你根本不能够apply这套想法。

接下来，有了 跟 以后，我们可以算出： ，这里面的除法代表element wise的除法。好，我们做完Normalization以后就得到了 ，经过Normalization以后 的 每一个dimension它的 ，你高兴的话就把它通过sigmoid得到A，然后再丢到下一个layer，Batch Normalization通常会每一个layer都做好，所以每一个layer的 ，在进入每一个激活函数之前，你都会做这一件事情。

它这边有一个其实大家可能比较不知道的事情是： 有batch Normalization的时候怎么作training？ 很多同学想法也许是跟原来没有做背Normalization没有什么不同。其实不是这样，真正在train这个batch Normalization的时候， 会把整个batch里面所有的data一起考虑 。我不知道大家听不听得懂我的意思，你train这个batch Normalization的时候，你要想成你有一个非常巨大的network，然后它的input就是 ，然后得到 ,中间它还会算两个东西 跟 ，它会产生 ， ，你一路backout回来的时候，他是会通过 ,通过 ，然后去update z的。

为什么这样？因为假设你不这么做，你把 跟 视为是一个常数。当你实际在train你的network的时候，你Backpropagation的时候，你改的这个 的值，你会改动这个 的值，改动这个 的值，其实你就等同于改动了 跟 的值。但是如果你在training的时候没有把这件事情考虑进去会是有问题的。所以其实在做batch Normalization的时候， 对 的影响是会被在training的时候考虑进去的。所以今天你要想成是你有一个非常巨大的network，input就是一整个batch，在Backpropagation的时候，它error signal也会从这个path（上图粗箭头的反向路径）回来，所以 对 跟 的影响是会在training的时候被考虑进去的，这样讲大家有问题吗？ 如果有问题，就忽略吧……

接下来继续，我们已经把 Normalize ；

但是有时候你会遇到的状况是，你可能不希望你的激活函数的input是 ，也许有些特别的激活函数，但我一下想不到是什么，他的mean和variance是别的值，performance更好。你可以再加上 跟 ，把你现在的distribution的mean和variance再做一下改动，你可以把你的 乘上这个 ，然后再加上 得到 ，然后再把 通过sigmoid函数，当做下一个layer的input，这个 跟 你就把它当做是network的参数，它也是可以跟着network一起被learn出来的。

这边有人可能会有问题是如果我今天的 正好等于 ， 正好等于 ，Normalization不就是有做跟没做一样吗？就是把 Normalize成 ，再把 Normalize成 ，但是如果今天 正好等于 ， 正好等于 的话就等于没有做事，确实是如此。但是加 和 跟 和 还是有不一样的地方，因为 和 它是受到data所影响。但是今天你的 和 是独立的，他是跟input的data是没有关系的，它是network自己加上去的，他是不会受到input的feature所影响的，所以它们还是有一些不一样的地方。

好，我们看一下在testing的时候怎么做，假设我们知道training什么时候怎么做，我们就train出一个network，其实它在train的时候它是考虑整个batch的，所以他其实要吃一整个batch才work。好，他得到一个 ，他会用 减掉 除以 ， 跟 是从一整个batch的data来的，然后他会得到 ，它会乘上 ，再加上 ， 和 是network参数一部分，得到的 。training的时候没有问题，testing的时候你就有问题了，因为你不知道怎么算 跟 ， 对不对？因为training的时候，你input一整个batch，算出一整个batch的 跟 。但是testing的时候你就有点问题，因为你只有一笔data进来，所以你估不出 跟 。

有一个ideal的solution是说：既然 跟 代表的是整个data set的feature的 均值和标准差 ，而且现在的training的process已经结束了，所以整个network的参数已经固定下来了，我们train好network以后再把它apply到整个training set上面，然后你就可以估测现在 的 跟 ，之前没有办法直接一次估出来，是因为我们network参数不断的在变，在你的training结束以后，把training里的参数已经确定好，你就可以算 的distribution，就可以估出 的 跟 。

这是一个理想的做法，在实做上有时候你没有办法这么做，一个理由是有时候你的training set太大，可能你把整个training set的data都倒出来再重新算一次 跟 ，也许你都不太想做，而另外一个可能是你的training的data是一笔一笔进来的，你并没有把data省下来，你data一个batch进来，你要备参数以后，那个batch就丢掉，你的训练资料量非常大，所以要训练是不省下来的，你每次只进来一个batch，所以也许你的training set根本就没有留下来，所以你也没有办法估测training set的 跟 ;

所以可行的solution是怎么做呢？这个critical 的solution是说把过去在update的过程中的 跟 都算出来，随着这个training的过程正确率会缓缓地上升，如上图红色框中图示：假设第一次取一个batch算出来是 ，第100次取一个batch算出来是 ……你可以说我把过去所有的 连起来当作是整个data的statistic，我这样做也不见得太好，为什么？因为今天在训练过程中参数是不断的变化，所以第一次地方算出来的 跟第100次算出来的 显然是差很多的，对不对？因为真正最后训练完的参数会比较接近100次得到的参数，第一次得到参数跟你训练时候得到参数差很多，所以这个地方的 跟你实际上你训练好的network以后，他会算出来的 的 是差很多的，所以在实做上你会给靠近training结束的这些 比较大的 weight ，然后给前面这些比较少的 weight 。

[转] 深入理解Batch Normalization批标准化

转自：https://www.cnblogs.com/guoyaohua/p/8724433.html

　　

郭耀华‘s Blog

欲穷千里目，更上一层楼
项目主页：https://github.com/guoyaohua/

• 博客园
• 首页
• 新随笔
• 联系
• 订阅
• 管理

欲穷千里目，更上一层楼
项目主页：https://github.com/guoyaohua/

• 博客园
• 首页
• 新随笔
• 联系
• 订阅
• 管理

【深度学习】深入理解Batch Normalization批标准化

 

这几天面试经常被问到BN层的原理，虽然回答上来了，但还是感觉答得不是很好，今天仔细研究了一下Batch Normalization的原理，以下为参考网上几篇文章总结得出。

　　Batch Normalization作为最近一年来DL的重要成果，已经广泛被证明其有效性和重要性。虽然有些细节处理还解释不清其理论原因，但是实践证明好用才是真的好，别忘了DL从Hinton对深层网络做Pre-Train开始就是一个经验领先于理论分析的偏经验的一门学问。本文是对论文《Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift》的导读。

　　机器学习领域有个很重要的假设：IID独立同分布假设，就是假设训练数据和测试数据是满足相同分布的，这是通过训练数据获得的模型能够在测试集获得好的效果的一个基本保障。那BatchNorm的作用是什么呢？BatchNorm就是在深度神经网络训练过程中使得每一层神经网络的输入保持相同分布的。

　　接下来一步一步的理解什么是BN。

　　为什么深度神经网络随着网络深度加深，训练起来越困难，收敛越来越慢？这是个在DL领域很接近本质的好问题。很多论文都是解决这个问题的，比如ReLU激活函数，再比如Residual Network，BN本质上也是解释并从某个不同的角度来解决这个问题的。

一、“Internal Covariate Shift”问题

　　从论文名字可以看出，BN是用来解决“Internal Covariate Shift”问题的，那么首先得理解什么是“Internal Covariate Shift”？

　　论文首先说明Mini-Batch SGD相对于One Example SGD的两个优势：梯度更新方向更准确；并行计算速度快；（为什么要说这些？因为BatchNorm是基于Mini-Batch SGD的，所以先夸下Mini-Batch SGD，当然也是大实话）；然后吐槽下SGD训练的缺点：超参数调起来很麻烦。（作者隐含意思是用BN就能解决很多SGD的缺点）

　　接着引入covariate shift的概念：如果ML系统实例集合<X,Y>中的输入值X的分布老是变，这不符合IID假设，网络模型很难稳定的学规律，这不得引入迁移学习才能搞定吗，我们的ML系统还得去学习怎么迎合这种分布变化啊。对于深度学习这种包含很多隐层的网络结构，在训练过程中，因为各层参数不停在变化，所以每个隐层都会面临covariate shift的问题，也就是在训练过程中，隐层的输入分布老是变来变去，这就是所谓的“Internal Covariate Shift”，Internal指的是深层网络的隐层，是发生在网络内部的事情，而不是covariate shift问题只发生在输入层。

　　然后提出了BatchNorm的基本思想：能不能让每个隐层节点的激活输入分布固定下来呢？这样就避免了“Internal Covariate Shift”问题了。

　　BN不是凭空拍脑袋拍出来的好点子，它是有启发来源的：之前的研究表明如果在图像处理中对输入图像进行白化（Whiten）操作的话——所谓白化，就是对输入数据分布变换到0均值，单位方差的正态分布——那么神经网络会较快收敛，那么BN作者就开始推论了：图像是深度神经网络的输入层，做白化能加快收敛，那么其实对于深度网络来说，其中某个隐层的神经元是下一层的输入，意思是其实深度神经网络的每一个隐层都是输入层，不过是相对下一层来说而已，那么能不能对每个隐层都做白化呢？这就是启发BN产生的原初想法，而BN也确实就是这么做的，可以理解为对深层神经网络每个隐层神经元的激活值做简化版本的白化操作。

二、BatchNorm的本质思想

　　BN的基本思想其实相当直观：因为深层神经网络在做非线性变换前的激活输入值（就是那个x=WU+B，U是输入）随着网络深度加深或者在训练过程中，其分布逐渐发生偏移或者变动，之所以训练收敛慢，一般是整体分布逐渐往非线性函数的取值区间的上下限两端靠近（对于Sigmoid函数来说，意味着激活输入值WU+B是大的负值或正值），所以这导致反向传播时低层神经网络的梯度消失，这是训练深层神经网络收敛越来越慢的本质原因，而BN就是通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布，其实就是把越来越偏的分布强制拉回比较标准的分布，这样使得激活输入值落在非线性函数对输入比较敏感的区域，这样输入的小变化就会导致损失函数较大的变化，意思是这样让梯度变大，避免梯度消失问题产生，而且梯度变大意味着学习收敛速度快，能大大加快训练速度。

　　THAT’S IT。其实一句话就是：对于每个隐层神经元，把逐渐向非线性函数映射后向取值区间极限饱和区靠拢的输入分布强制拉回到均值为0方差为1的比较标准的正态分布，使得非线性变换函数的输入值落入对输入比较敏感的区域，以此避免梯度消失问题。因为梯度一直都能保持比较大的状态，所以很明显对神经网络的参数调整效率比较高，就是变动大，就是说向损失函数最优值迈动的步子大，也就是说收敛地快。BN说到底就是这么个机制，方法很简单，道理很深刻。

　　上面说得还是显得抽象，下面更形象地表达下这种调整到底代表什么含义。

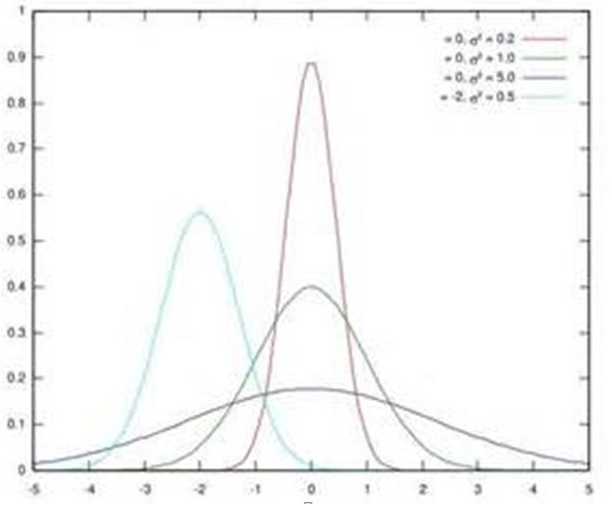
  图1  几个正态分布

　　假设某个隐层神经元原先的激活输入x取值符合正态分布，正态分布均值是-2，方差是0.5，对应上图中最左端的浅蓝色曲线，通过BN后转换为均值为0，方差是1的正态分布（对应上图中的深蓝色图形），意味着什么，意味着输入x的取值正态分布整体右移2（均值的变化），图形曲线更平缓了（方差增大的变化）。这个图的意思是，BN其实就是把每个隐层神经元的激活输入分布从偏离均值为0方差为1的正态分布通过平移均值压缩或者扩大曲线尖锐程度，调整为均值为0方差为1的正态分布。

　　那么把激活输入x调整到这个正态分布有什么用？首先我们看下均值为0，方差为1的标准正态分布代表什么含义：

 

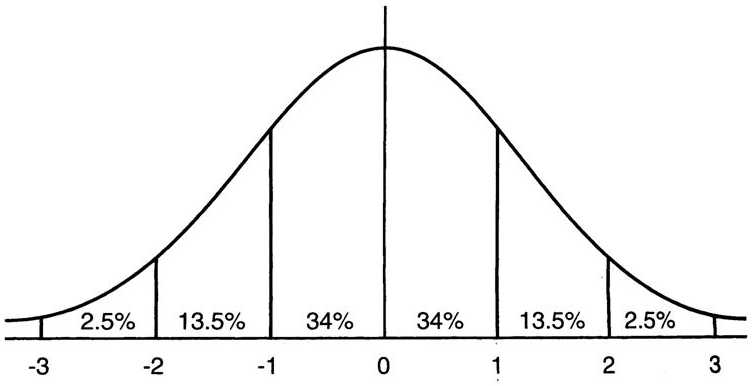
图2  均值为0方差为1的标准正态分布图

 

　　这意味着在一个标准差范围内，也就是说64%的概率x其值落在[-1,1]的范围内，在两个标准差范围内，也就是说95%的概率x其值落在了[-2,2]的范围内。那么这又意味着什么？我们知道，激活值x=WU+B,U是真正的输入，x是某个神经元的激活值，假设非线性函数是sigmoid，那么看下sigmoid(x)其图形：

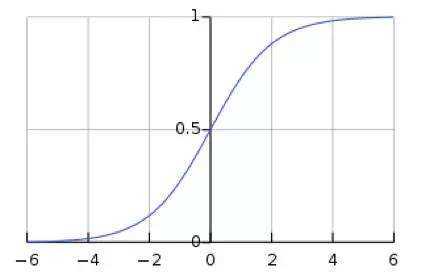
图3. Sigmoid(x)

及sigmoid(x)的导数为：G’=f(x)*(1-f(x))，因为f(x)=sigmoid(x)在0到1之间，所以G’在0到0.25之间，其对应的图如下：

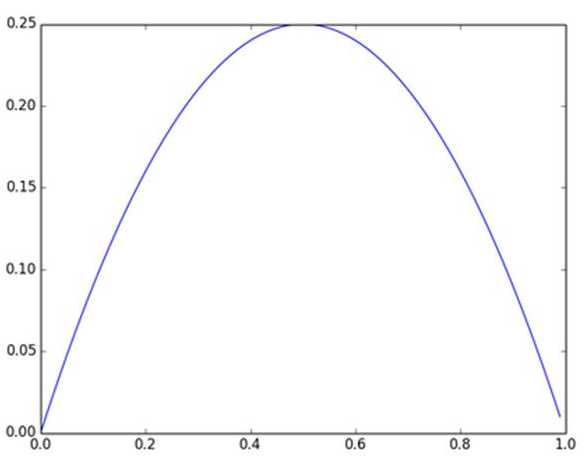
图4  Sigmoid(x)导数图

　　假设没有经过BN调整前x的原先正态分布均值是-6，方差是1，那么意味着95%的值落在了[-8,-4]之间，那么对应的Sigmoid（x）函数的值明显接近于0，这是典型的梯度饱和区，在这个区域里梯度变化很慢，为什么是梯度饱和区？请看下sigmoid(x)如果取值接近0或者接近于1的时候对应导数函数取值，接近于0，意味着梯度变化很小甚至消失。而假设经过BN后，均值是0，方差是1，那么意味着95%的x值落在了[-2,2]区间内，很明显这一段是sigmoid(x)函数接近于线性变换的区域，意味着x的小变化会导致非线性函数值较大的变化，也即是梯度变化较大，对应导数函数图中明显大于0的区域，就是梯度非饱和区。

　　从上面几个图应该看出来BN在干什么了吧？其实就是把隐层神经元激活输入x=WU+B从变化不拘一格的正态分布通过BN操作拉回到了均值为0，方差为1的正态分布，即原始正态分布中心左移或者右移到以0为均值，拉伸或者缩减形态形成以1为方差的图形。什么意思？就是说经过BN后，目前大部分Activation的值落入非线性函数的线性区内，其对应的导数远离导数饱和区，这样来加速训练收敛过程。

　　但是很明显，看到这里，稍微了解神经网络的读者一般会提出一个疑问：如果都通过BN，那么不就跟把非线性函数替换成线性函数效果相同了？这意味着什么？我们知道，如果是多层的线性函数变换其实这个深层是没有意义的，因为多层线性网络跟一层线性网络是等价的。这意味着网络的表达能力下降了，这也意味着深度的意义就没有了。所以BN为了保证非线性的获得，对变换后的满足均值为0方差为1的x又进行了scale加上shift操作(y=scale*x+shift)，每个神经元增加了两个参数scale和shift参数，这两个参数是通过训练学习到的，意思是通过scale和shift把这个值从标准正态分布左移或者右移一点并长胖一点或者变瘦一点，每个实例挪动的程度不一样，这样等价于非线性函数的值从正中心周围的线性区往非线性区动了动。核心思想应该是想找到一个线性和非线性的较好平衡点，既能享受非线性的较强表达能力的好处，又避免太靠非线性区两头使得网络收敛速度太慢。当然，这是我的理解，论文作者并未明确这样说。但是很明显这里的scale和shift操作是会有争议的，因为按照论文作者论文里写的理想状态，就会又通过scale和shift操作把变换后的x调整回未变换的状态，那不是饶了一圈又绕回去原始的“Internal Covariate Shift”问题里去了吗，感觉论文作者并未能够清楚地解释scale和shift操作的理论原因。

三、训练阶段如何做BatchNorm

　　上面是对BN的抽象分析和解释，具体在Mini-Batch SGD下做BN怎么做？其实论文里面这块写得很清楚也容易理解。为了保证这篇文章完整性，这里简单说明下。

　　假设对于一个深层神经网络来说，其中两层结构如下：

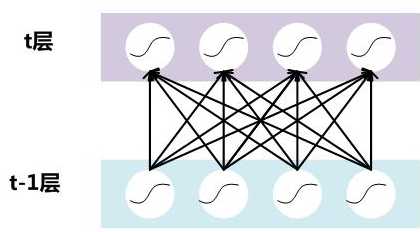
  图5  DNN其中两层

　　要对每个隐层神经元的激活值做BN，可以想象成每个隐层又加上了一层BN操作层，它位于X=WU+B激活值获得之后，非线性函数变换之前，其图示如下：

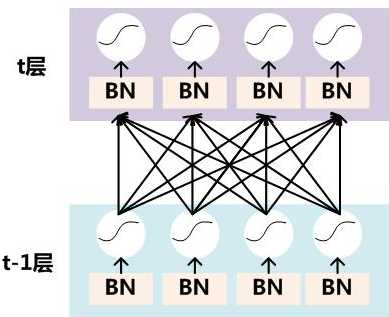
  图6. BN操作

　　对于Mini-Batch SGD来说，一次训练过程里面包含m个训练实例，其具体BN操作就是对于隐层内每个神经元的激活值来说，进行如下变换：

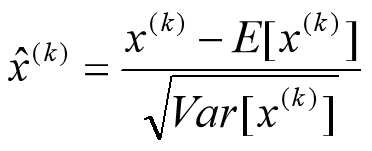
　　要注意，这里t层某个神经元的x(k)不是指原始输入，就是说不是t-1层每个神经元的输出，而是t层这个神经元的线性激活x=WU+B，这里的U才是t-1层神经元的输出。变换的意思是：某个神经元对应的原始的激活x通过减去mini-Batch内m个实例获得的m个激活x求得的均值E(x)并除以求得的方差Var(x)来进行转换。

　　上文说过经过这个变换后某个神经元的激活x形成了均值为0，方差为1的正态分布，目的是把值往后续要进行的非线性变换的线性区拉动，增大导数值，增强反向传播信息流动性，加快训练收敛速度。但是这样会导致网络表达能力下降，为了防止这一点，每个神经元增加两个调节参数（scale和shift），这两个参数是通过训练来学习到的，用来对变换后的激活反变换，使得网络表达能力增强，即对变换后的激活进行如下的scale和shift操作，这其实是变换的反操作：

　　BN其具体操作流程，如论文中描述的一样：

 

　　过程非常清楚，就是上述公式的流程化描述，这里不解释了，直接应该能看懂。

四、BatchNorm的推理(Inference)过程

　　BN在训练的时候可以根据Mini-Batch里的若干训练实例进行激活数值调整，但是在推理（inference）的过程中，很明显输入就只有一个实例，看不到Mini-Batch其它实例，那么这时候怎么对输入做BN呢？因为很明显一个实例是没法算实例集合求出的均值和方差的。这可如何是好？

　　既然没有从Mini-Batch数据里可以得到的统计量，那就想其它办法来获得这个统计量，就是均值和方差。可以用从所有训练实例中获得的统计量来代替Mini-Batch里面m个训练实例获得的均值和方差统计量，因为本来就打算用全局的统计量，只是因为计算量等太大所以才会用Mini-Batch这种简化方式的，那么在推理的时候直接用全局统计量即可。

　　决定了获得统计量的数据范围，那么接下来的问题是如何获得均值和方差的问题。很简单，因为每次做Mini-Batch训练时，都会有那个Mini-Batch里m个训练实例获得的均值和方差，现在要全局统计量，只要把每个Mini-Batch的均值和方差统计量记住，然后对这些均值和方差求其对应的数学期望即可得出全局统计量，即：

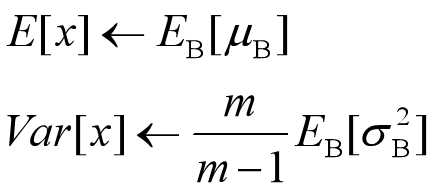
　　有了均值和方差，每个隐层神经元也已经有对应训练好的Scaling参数和Shift参数，就可以在推导的时候对每个神经元的激活数据计算NB进行变换了，在推理过程中进行BN采取如下方式：

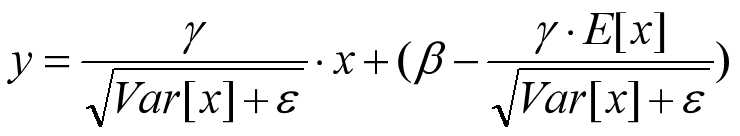
　　这个公式其实和训练时

　　是等价的，通过简单的合并计算推导就可以得出这个结论。那么为啥要写成这个变换形式呢？我猜作者这么写的意思是：在实际运行的时候，按照这种变体形式可以减少计算量，为啥呢？因为对于每个隐层节点来说：

　　　　　　　　　　

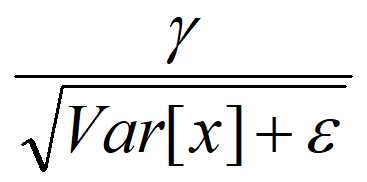
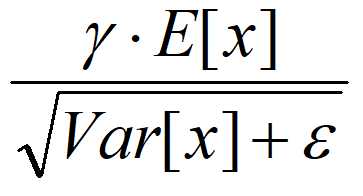
　　都是固定值，这样这两个值可以事先算好存起来，在推理的时候直接用就行了，这样比原始的公式每一步骤都现算少了除法的运算过程，乍一看也没少多少计算量，但是如果隐层节点个数多的话节省的计算量就比较多了。

五、BatchNorm的好处

　　BatchNorm为什么NB呢，关键还是效果好。①不仅仅极大提升了训练速度，收敛过程大大加快；②还能增加分类效果，一种解释是这是类似于Dropout的一种防止过拟合的正则化表达方式，所以不用Dropout也能达到相当的效果；③另外调参过程也简单多了，对于初始化要求没那么高，而且可以使用大的学习率等。总而言之，经过这么简单的变换，带来的好处多得很，这也是为何现在BN这么快流行起来的原因。