求这个c语言题目的解题思路和解法?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了求这个c语言题目的解题思路和解法?相关的知识,希望对你有一定的参考价值。
2003年突发的非典型肺炎(SARS)是一种病源还不完全了解的新型传染病,需要隔离所有疑似病例。在N大学,有许多学生团体,一个学生可以加入多个团体,同一个学生团体内部成员被认为是经常接触的。N大学为了应付SARS,规定若一个学生被认为是疑似病例,则他所在团体的所有学生都被认为是疑似病例。现在需要你编写一个程序,在发现一个学生是疑似病例后,找到所有与之直接或间接接触过的疑似病例。可以设每一名学生用数字0到n-1编号,输入有学生总数n,学生团体数k,每个学生团体的人数和成员的编号,可能是SARS疑似病例的学生编号,输出所有找到的疑似病例学生编号。例如,
输入数据如下:
1004 //100名学生,4个学生团体;
2 1 2 //第一个学生团体有2人,是编号1和2的两位学生,以下三个团体类似;
5 10 13 11 12 14
2 0 1
2 99 2
0 //现在发现编号0的学生是疑似病例。
这时应输出如下:
4,0,1,2,99表示发现有4位疑似病例,是编号是0,1,2,99的
尽量多注释每个步骤,我是个菜鸟。
求解整个算法
1.采用二维数组(int型)存放所有学生编号,一行为一个团体。
2.用一个一维数组存放所有疑似病的学生编号
3.按编号查询所有团体的学生,
4.查找到后,即将该行所有编号存入2.中的数组
5.输出2.中的数组即可。
编写程序时,第4.和5.采用递归调用。
程序如下(该程序已经在WIN-TC上通过)
#include<stdio.h>
#include<stdlib.h>
#define N 100 /*学生总人数的最高限制数额*/
#define M 10 /*团体的个数的最高限制数额*/
#define S 10 /*团体的人数的最高限额*/
int num[S+1]; /*存放疑似病历的学生编号*/
int count; /*累计有疑似病历学生的数量*/
void findnumber(int k,int groupn,int a[][S+1])/*查找并保存所有关联学生编号*/
int i,j,flag;
int da[S],tem,n;
for(i=0;i<groupn;i++) /*对每个团体做如下操作*/
if(a[i][1]<0)continue;/*表示对已经确定的团体不再重复操作*/
tem=a[i][0];
flag=0;
for(j=1;j<=tem;j++) /*搜索团体的每一个编号,看是否与欲查编号k是否相符*/
if(a[i][j]==k)
flag=1; /*如果相符则记flag为1,以作为下面操作的条件*/
break;
if(flag) /*flag不为零则表示该团体包含疑似病的学生编号,进行如下的操作:*/
for(j=1;j<=tem;j++) /*将该团体的所有编号保存*/
da[j-1]=a[i][j];
for(n=0;n<count;n++) /*这一循环是为了保证已经记录过的编号不再重复录入*/
if(num[n]==a[i][j])
n=-1;break;
if(n>=0)num[count++]=a[i][j];
a[i][j]=-1; /*对已经确定的团体在保存后赋负值,以便后面不再重复*/
for(j=0;j<tem;j++)
findnumber(da[j],groupn,a); /*对该团体的其他编号再一次递归调用*/
main()
int students[N],number[M],data[M][S+1];
int studentsum,groupsum,i,j,k;
char str[10];
/*输入学生总人数和团体的个数*/
scanf("%d %d",&studentsum,&groupsum);
/*输入每个团体的学生的编号*/
for(i=0;i<groupsum;i++)
printf("NO.%d:(输入y或Y结束)\n",i+1);/*提示以下对第i个团体进行录入*/
scanf("%d",&data[i][0]); /*输入团体包含的人数*/
for(j=1;j<=S;j++) /*录入一个团体的每个学生的编号*/
scanf("%s",str);
if(stricmp(str,"y")==0)break; /*检查是否输入了y 或Y,如是则表示本团体录入完成*/
data[i][j]=atoi(str);
/*输入第一个疑似病的学生编号*/
printf("numbering=");
scanf("%d",&k);
/*以下开始查找*/
count=0; /*记数器初始化清零*/
findnumber(k,groupsum,data);/*采用递归函数找所有相关联的团体的学生编号*/
/*将查找结果输出*/
printf("\n%d ",count); /*先输出所有有关联的学生的总数*/
for(i=0;i<count;i++) /*在总数后面罗列所有编号*/
printf("%d ",num[i]);
getch(); /*显示结束后,等待按任意键后程序*/
return 0;
参考技术A
你只要思路?可以使用图结构,邻接表存储方式。把数据处理好以后,一旦输出某个编号,然后找到对应编号,对图进行深度搜索。可以使用深度优先,广度优先也可以。
不知道你这是用于什么的,要说出具体来源才好针对性根据要求写代码或提供更多思路。
----------------------------------------------------------------------------------------------------------------------------------
************************二次回答***********************************************
楼主也不追问一下,你追问了,回答的才知道是否还有回答的必要。
下面的程序大致能实现,但是还是不清楚你程序的用途,比如是什么自测平台的话还得看输入输出格式,其它的话还得增加对错误的判断,比如内存申请失败,内存是否多余等等。
程序见附件。
C语言课程设计——25道蓝桥杯练习题
文章目录
- 一、基础练习
- 二、算法提高
- 三、历届试题
一、基础练习
1.fib数列
题目
题目链接
Fibonacci数列的递推公式为:Fn=Fn-1+Fn-2,其中F1=F2=1。当n比较大时,Fn也非常大,现在我们想知道,Fn除以10007的余数是多少。
数据规模与约定
1 <= n <= 1,000,000。
解题思路
很明显,数据规模并不大,O(n)时间复杂度便可解决。
但如果数据规模非常庞大,我们可以利用到下面这张图的矩阵递推公式再根据矩阵快速幂解决:
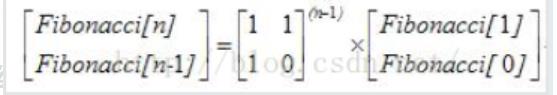
解题代码
解法一(简单递推):时间复杂度O(n)
适用于数据量少于10^8的情况
#include <stdio.h>
const int MOD = 10007;
int main()
int n;
scanf("%d", &n);
int a=1,b=1;
if(n<=2)printf("1");
else
int tmp;
int i;
for(i=3;i<=n;i++)
tmp = b;
b = (a+b)%MOD;
a = tmp;
printf("%d",b);
return 0;
解法二(矩阵快速幂):时间复杂度O(logn)
适用于数据量大于10^8的情况
//
// Created by Alone on 2021/11/19.
//
#include <bits/stdc++.h>
using namespace std;
typedef long long ll ;
//TODO To design a matrix class to solve this problem
class Matrix
ll** date;
int m;
int n;
public: static const int MOD;
public:
Matrix(ll** rec,int n,int m):date(rec),n(n),m(m)//C format to init
Matrix():date(NULL),m(0),n(0) //aefault
Matrix(Matrix& b):n(b.n),m(b.m)//copy struct
assert(b.date!=NULL && b.n>0 && b.m>0);
date = new ll*[n];
copy(b.date,b.date+n,date);
for(int i=0;i<n;i++)
date[i] = new ll[m];
copy(b.date[i],b.date[i]+m,date[i]);
~Matrix()//destruct
assert(date!=NULL && n>0 && m>0);
for (int i = n-1; i >=0 ; --i)
delete [] date[i];
delete[] date;
Matrix& operator*(Matrix& b)//TODO operator* to overload
assert(b.date!=NULL && date!=NULL && m==b.n);
ll tmp[n][b.m];
for(int i=0;i<n;i++)
for(int j=0;j<b.m;j++)
ll sum = 0;
for(int k=0;k<m;k++)
sum = (sum + date[i][k]*b.date[k][j])%MOD;
tmp[i][j] = sum;
this->m = b.m;
for(int i=0;i<n;i++)
for (int j = 0; j < m; ++j)
date[i][j] = tmp[i][j];
return *this;
void init()//TODO initialized to unit matrix
assert(date!=NULL && n>0 && m>0);
for (int i = 0; i < n; ++i)
for (int j = 0; j < m; ++j)
if(i==j)date[i][j] = 1;
else date[i][j] = 0;
void quickPow(ll c)//TODO quick pow for matrix
if(c==1||c<0)return;
if(c==0)
init();
return;
Matrix tmp(*this);
init();
while (c)
if(c&1)
*this = *this * tmp;
c >>= 1;
tmp = tmp*tmp;
void print()//TODO to print this matrix
for(int i=0;i<n;i++)
for(int j=0;j<m;j++)
cout<<date[i][j]<<' ';
cout<<endl;
int get(int x,int y)//TODO provide access to the outside
assert(date!=NULL && x<n && y<m);
return date[x][y];
;
const int Matrix::MOD = 1007;//TODO set the factor for mod operation
int main()
ll c;
cin>>c;
ll** matrix = new ll*[2];
matrix[0] = new ll[2]1,1;
matrix[1] = new ll[2]1,0;
Matrix mat(matrix,2,2);
mat.quickPow(c-1);
ll** res = new ll*[2];
res[0] = new ll[1]1;
res[1] = new ll[1]1;
Matrix fib(res,2,1);
Matrix ret(mat*fib);
cout<<ret.get(1,0);
return 0;
2.闰年判断
题目
解题思路
只要挑选处闰年即可,闰年有个判断方式将其判断:
关于闰年的解释:
- 普通年份能被4整除,且不能被100整除的,是闰年。( 如2004年就是闰年)
- 世纪年份能被400整除的是闰年。( 如2000年是闰年,1900年不是闰年)
如果年份是闰年,那么它的二月份就会比平常多1天。
解题代码
#include<stdio.h>
int main()
int n;
const char* res[]= "no","yes";
scanf("%d",&n);
int index = 0;
if(n%400==0||(n%4==0&&n%100!=0))
index = 1;
fputs(res[index],stdout);
return 0;
3. 数列特征
题目
解题思路
求一个数组的最大值和最小值以及所有数字的和。。
解题代码
#include<iostream>
#include<algorithm>
#include<limits>
using namespace std;
int main()
int n;
cin>>n;
int nums[n];
int mx=INT_MIN,mn=INT_MAX,sum = 0;
for(int i=0;i<n;i++)
cin>>nums[i];
mx = max(mx,nums[i]);
mn = min(mn,nums[i]);
sum += nums[i];
printf("%d\\n%d\\n%d",mx,mn,sum);
return 0;
4.查找整数
题目
解题思路
按照题目意思来就行,直接查找第一次出现的位置即可。
解题代码
解法一:C风格
#include <iostream>
using namespace std;
int main()
int n,target;
int res = -1;
cin>>n;
int nums[n];
for(int i=0;i<n;i++)
cin>>nums[i];
cin>>target;
for (int i = 0; i < n; ++i)
if(nums[i]==target)
res = i+1;
break;
cout<<res;
return 0;
解法二:C++风格
由于C++98不支持lamda表达式,所以需要把传入的函数单独写出来了。
#include <bits/stdc++.h>
using namespace std;
void input(int& a)cin>>a;
int main()
int n,target,res;
cin>>n;
int nums[n];
for_each(nums,nums+n,input);
cin>>target;
res = find(nums,nums+n,target)-nums+1;
if(res>n)
res = -1;
cout<<res;
return 0;
C++11风格
#include <bits/stdc++.h>
using namespace std;
int main()
int n,target;
int res;
cin>>n;
int nums[n];
for_each(nums,nums+n,[](int& a)cin>>a;);
cin>>target;
res = find(nums,nums+n,target)-nums+1;
if(res>n)
res = -1;
cout<<res;
return 0;
5.杨辉三角形
题目

解题思路
根据杨辉三角的性质来做,对于杨辉三角第 i 行、第 j 列的元素,我们用 dp[i][j] 来进行表示,那么有以下关系:
d
p
[
i
]
[
j
]
=
d
p
[
i
−
1
]
[
j
]
+
d
p
[
i
−
1
]
[
j
−
1
]
(
0
<
j
<
m
)
1
(
j
=
0
,
j
=
m
)
dp[i][j] = \\left\\ \\beginarrayl dp[i-1][j]+dp[i-1][j-1](0<j<m) \\\\ 1\\quad\\quad\\quad\\quad\\quad\\quad\\quad\\quad\\quad\\quad\\quad(j=0,j=m) \\endarray \\right.
dp[i][j]=dp[i−1][j]+dp[i−1][j−1](0<j<m)1(j=0,j=m)
解题代码