第十四届蓝桥杯大赛软件赛省赛JavaB组解析
Posted 小羊不会飞
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了第十四届蓝桥杯大赛软件赛省赛JavaB组解析相关的知识,希望对你有一定的参考价值。
目录
说在前面
比赛结束啦,可能这是本科生涯的最后一次蓝桥杯啦!赛前也刷了一部分的题,不管最后能不能相约北京,还是要感谢我执梗举办的三十天打卡活动,辛苦啦!
我把这段时间刷的题也也整理成了一个小专栏:《23年蓝桥杯刷题30天打卡》
关于这次蓝桥杯,比赛的时候没有看D题,G和H花了好长时间,呜呜....,等比赛结束的时候边走边看题才知道是送分题,考后相当于是补题了,好遗憾,痛失10分,也许人生就是这样,十之八九是遗憾,但这又有何妨呢,前方康庄大道,还有很多美好的事情等着我呢!!!
下面就把这次我看过的并且感觉能做的题目写一下吧,如有错误,欢迎评论区指正!!
试题 A: 阶乘求和
【问题描述】 令 S = 1! + 2! + 3! + ... + 202320232023! ,求 S 的末尾 9 位数字。 提示:答案首位不为 0 。 【答案提交】 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
代码:
/**
* @author yx
* @date 2023-04-08 9:11
*/
public class t1
public static void main(String[] args)
// 420940313
long ans=0;
long temp=1000000000;
long temp1=1;
for (long i = 1; i <= 202320232023L ; i++)
temp1=((temp1%temp)*(i%temp))%temp;
ans=(ans%temp+temp1%temp)%temp;
System.out.println("temp1是:"+temp1+" ans是:"+ans+" i是:"+i);
// System.out.println("答案是:"+ans);
题目分析:
答案是:420940313
- 这道题目最后给的是202320232023的阶乘,这玩意要是用电脑暴力解,估计要很长时间(我一开始也是无脑暴力,但是感觉要好久)
- 这题完全不需要开到202320232023,因为从39!开始,后面阶乘和的末尾9位数字就不发生改变了
试题 B: 幸运数字
试题 B: 幸运数字 本题总分: 5 分 【问题描述】 哈沙德数是指在某个固定的进位制当中,可以被各位数字之和整除的正整 数。例如 126 是十进制下的一个哈沙德数,因为 (126) 10 mod (1+2+6) = 0 ; 126 也是八进制下的哈沙德数,因为 (126) 10 = (176) 8 , (126) 10 mod (1 + 7 + 6) = 0 ; 同时 126 也是 16 进制下的哈沙德数,因为 (126) 10 = (7 e ) 16 , (126) 10 mod (7 + e ) = 0 。小蓝认为,如果一个整数在二进制、八进制、十进制、十六进制下均为 哈沙德数,那么这个数字就是幸运数字,第 1 至第 10 个幸运数字的十进制表示 为: 1 , 2 , 4 , 6 , 8 , 40 , 48 , 72 , 120 , 126 . . . 。现在他想知道第 2023 个幸运数 字是多少?你只需要告诉小蓝这个整数的十进制表示即可。 【答案提交】 这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一 个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
代码:
import java.awt.*;
/**
* @author yx
* @date 2023-04-08 9:13
*/
public class t2
public static void main(String[] args)
int ans=0;
int i=0;
while (true)
i++;
if(isCheck(i))
ans++;
System.out.println(i+"为第"+ans+"个");
if(ans==2023)
break;
System.out.println("答案是:"+i);
static boolean isCheck(int n)
String temp1=Integer.toString(n,2);
String temp2=Integer.toString(n,8);
String temp3=n+"";
String temp4=Integer.toString(n,16);
int temp_1=0;
int temp_2=0;
int temp_3=0;
int temp_4=0;
for (int i = 0; i < temp1.length(); i++)
temp_1+=Integer.parseInt(temp1.substring(i,i+1));
if(n%temp_1!=0)
return false;
for (int i = 0; i < temp2.length() ;i++)
temp_2+=Integer.parseInt(temp2.substring(i,i+1));
if(n%temp_2!=0)
return false;
for (int i = 0; i < temp3.length(); i++)
temp_3+=Integer.parseInt(temp3.substring(i,i+1));
if(n%temp_3!=0)
return false;
for (int i = 0; i < temp4.length(); i++)
if((temp4.substring(i,i+1)).toCharArray()[0]>='a')
temp_4 += (temp4.substring(i,i+1)).toCharArray()[0]-'a'+10;
else
temp_4 += Integer.parseInt(temp4.substring(i, i + 1));
if(n%temp_4!=0)
return false;
return true;
题目分析:
答案是:215040
- 直接把数先进制转换,然后求数位和,判读能否整除数位和就好了
- 这题本质考一个进制转换,如果会用Java的API就很简单,前两天我在算法组会分享的时候刚好讲过,还写了题解,还上了热榜,哈哈哈,下面链接的第五题
试题 D: 矩形总面积
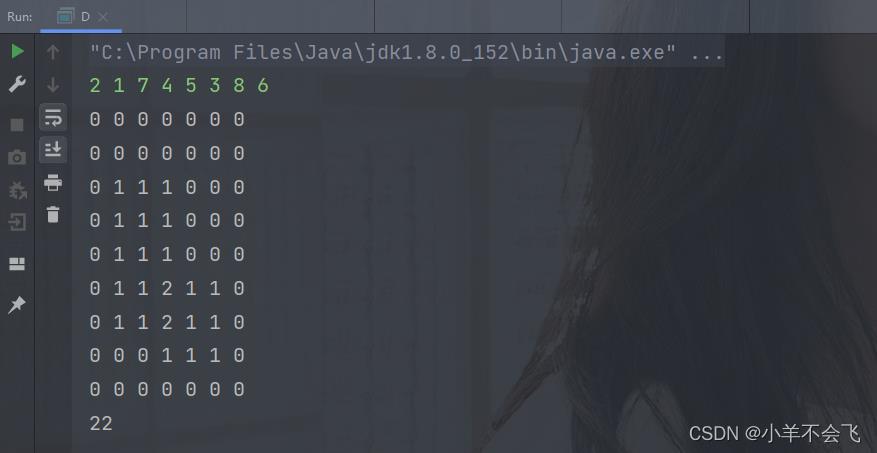
【问题描述】 平面上有个两个矩形 R 1 和 R 2 ,它们各边都与坐标轴平行。设 ( x 1 , y 1 ) 和 ( x 2 , y 2 ) 依次是 R 1 的左下角和右上角坐标, ( x 3 , y 3 ) 和 ( x 4 , y 4 ) 依次是 R 2 的左下 角和右上角坐标,请你计算 R 1 和 R 2 的总面积是多少? 注意:如果 R 1 和 R 2 有重叠区域,重叠区域的面积只计算一次。 【输入格式】 输入只有一行,包含 8 个整数,依次是: x 1 , y 1 , x 2 , y 2 , x 3 , y 3 , x 4 和 y 4 。 【输出格式】 一个整数,代表答案。 【样例输入】 2 1 7 4 5 3 8 6 【样例输出】 22 【样例说明】 样例中的两个矩形如图所示:【评测用例规模与约定】 对于 20 % 的数据, R 1 和 R 2 没有重叠区域。 对于 20 % 的数据,其中一个矩形完全在另一个矩形内部。 对于 50 % 的数据,所有坐标的取值范围是 [0 , 10 ^3 ] 。 对于 100 % 的数据,所有坐标的取值范围是 [0 , 10^ 5 ] 。
代码:
import java.io.*;
/**
* @author yx
* @date 2023-04-08 13:57
*/
public class D
static PrintWriter out =new PrintWriter(System.out);
static BufferedReader ins=new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer in=new StreamTokenizer(ins);
public static void main(String[] args) throws IOException
String[] sp=ins.readLine().split(" ");
int x1=Integer.parseInt(sp[0]);
int y1=Integer.parseInt(sp[1]);
int x2=Integer.parseInt(sp[2]);
int y2=Integer.parseInt(sp[3]);
int x3=Integer.parseInt(sp[4]);
int y3=Integer.parseInt(sp[5]);
int x4=Integer.parseInt(sp[6]);
int y4=Integer.parseInt(sp[7]);
long ans=0;
int max_X=Math.max(Math.max(x1,x2),Math.max(x3,x4));
int max_Y=Math.max(Math.max(y1,y2),Math.max(y3,y4));
int max=Math.max(max_X,max_Y);
int[][] Map=new int[max+1][max+1];
for (int i = y1; i <= y2-1 ; i++)
for (int j = x1; j <= x2-1 ; j++)
Map[i][j]+=1;
for (int i = y3; i <= y4-1 ; i++)
for (int j = x3; j <= x4-1 ; j++)
Map[i][j]+=1;
for (int i = 0; i <= max_X ; i++)
for (int j = 0; j <= max_Y ; j++)
// System.out.print(Map[j][i]+" ");
if(Map[j][i]>=1)
ans++;
// System.out.println();
System.out.println(ans);
题目分析:
- 这题就是直接暴力模拟(比赛的时候看了一眼题目就直接跳过了,哭死),赛后十分钟解决
- 先定义一个int[][]Map,然后遍历两块矩阵,把它们的覆盖的区域全部+1,属于矩阵区域但是不重合的地方Map值为1,重合的地方加了两次其Map值会变成2,不属于矩阵区间的范围当然为0
- 最后遍历二维数组Map,统计Map值>=1的个数就是答案
试题 G: 买二赠一
【问题描述】 某商场有 N 件商品,其中第 i 件的价格是 A i 。现在该商场正在进行 “ 买二 赠一 ” 的优惠活动,具体规则是: 每购买 2 件商品,假设其中较便宜的价格是 P (如果两件商品价格一样, 则 P 等于其中一件商品的价格),就可以从剩余商品中任选一件价格不超过 P 2 的商品,免费获得这一件商品。可以通过反复购买 2 件商品来获得多件免费商 品,但是每件商品只能被购买或免费获得一次。 小明想知道如果要拿下所有商品(包含购买和免费获得),至少要花费多少 钱? 【输入格式】 第一行包含一个整数 N 。 第二行包含 N 个整数,代表 A 1 , A 2 , A 3 , . . . , A N 。 【输出格式】 输出一个整数,代表答案。 【样例输入】 7 1 4 2 8 5 7 1 【样例输出】 25 试题 G: 买二赠一 13 第十四届蓝桥杯大赛软件赛省赛 Java 大学 B 组 【样例说明】 小明可以先购买价格 4 和 8 的商品,免费获得一件价格为 1 的商品;再后 买价格为 5 和 7 的商品,免费获得价格为 2 的商品;最后单独购买剩下的一件 价格为 1 的商品。总计花费 4 + 8 + 5 + 7 + 1 = 25 。不存在花费更低的方案。 【评测用例规模与约定】 对于 30 % 的数据, 1 ≤ N ≤ 20 。 对于 100 % 的数据, 1 ≤ N ≤ 5 × 10 5 , 1 ≤ A i ≤ 10 9 。
代码:
import java.io.*;
import java.util.ArrayList;
import java.util.Collections;
/**
* @author yx
* @date 2023-04-08 11:31
*/
public class G3
static PrintWriter out = new PrintWriter(System.out);
static BufferedReader ins = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer in = new StreamTokenizer(ins);
public static void main(String[] args) throws IOException
String s = ins.readLine();
int N = Integer.parseInt(s);
String[] sp = ins.readLine().split(" ");
ArrayList<Integer> list = new ArrayList<>();
long ans = 0;
for (int i = 0; i < N; i++)
list.add(Integer.parseInt(sp[i]));
Collections.sort(list);
for (int i = 0; list.size()>0 ; i++)
int a1 = 0;
int a2 = 0;
a1 = list.get(list.size() - 1);
list.remove(list.size() - 1);
if(list.size() - 1>=0)
a2 = list.get(list.size() - 1);
list.remove(list.size() - 1);
int mid = a2 / 2;
int length=list.size();
for (int j = length-1; j >= 0; j--)
if (list.get(j) <= mid)
list.remove(j);
break;
ans += (a1 + a2);
out.println(ans);
out.flush();
题目分析:
用队列的思想,不过我用的是ArrayList实现
- 首先用链表接收数据,对其进行排序,从大的开始买,才能让P/2尽可能大,然后才能让自己收益尽可能大
- 从最大的元素的开始遍历,取最大的两个元素A1、A2(A1>A2)计入总花费,然后把这两个元素出队,找队列中小于等于A2/2的最大元素,它可以白嫖,然后把它出队
- 找A2/2元素可以用二分优化,不过我当时神经有点紧绷,二分报错,所以直接从A2开始往后遍历了,复杂度会高一点
试题 H: 合并石子
【问题描述】 在桌面从左至右横向摆放着 N 堆石子。每一堆石子都有着相同的颜色,颜 色可能是颜色 0 ,颜色 1 或者颜色 2 中的其中一种。 现在要对石子进行合并,规定每次只能选择位置相邻并且颜色相同的两堆 石子进行合并。合并后新堆的相对位置保持不变,新堆的石子数目为所选择的 两堆石子数目之和,并且新堆石子的颜色也会发生循环式的变化。具体来说: 两堆颜色 0 的石子合并后的石子堆为颜色 1 ,两堆颜色 1 的石子合并后的石子 堆为颜色 2 ,两堆颜色 2 的石子合并后的石子堆为颜色 0 。本次合并的花费为所 选择的两堆石子的数目之和。 给出 N 堆石子以及他们的初始颜色,请问最少可以将它们合并为多少堆石 子?如果有多种答案,选择其中合并总花费最小的一种,合并总花费指的是在 所有的合并操作中产生的合并花费的总和。 【输入格式】 第一行一个正整数 N 表示石子堆数。 第二行包含 N 个用空格分隔的正整数,表示从左至右每一堆石子的数目。 第三行包含 N 个值为 0 或 1 或 2 的整数表示每堆石头的颜色。 【输出格式】 一行包含两个整数,用空格分隔。其中第一个整数表示合并后数目最少的 石头堆数,第二个整数表示对应的最小花费。 【样例输入】 5 5 10 1 8 6 1 1 0 2 2 试题 H: 合并石子 15 第十四届蓝桥杯大赛软件赛省赛 Java 大学 B 组 【样例输出】 2 44 【样例说明】上图显示了两种不同的合并方式。其中节点中标明了每一堆的石子数目, 在方括号中标注了当前堆石子的颜色属性。左图的这种合并方式最终剩下了两 堆石子,所产生的合并总花费为 15 + 14 + 15 = 44 ;右图的这种合并方式最终 也剩下了两堆石子,但产生的合并总花费为 14 + 15 + 25 = 54 。综上所述,我 们选择合并花费为 44 的这种方式作为答案。 【评测用例规模与约定】 对于 30 % 的评测用例, 1 ≤ N ≤ 10 。 对于 50 % 的评测用例, 1 ≤ N ≤ 50 。 对于 100 % 的评测用例, 1 ≤ N ≤ 300 , 1 ≤ 每堆石子的数目 ≤ 1000 。
代码:
import java.io.*;
import java.util.ArrayList;
import java.util.Collections;
import java.util.LinkedList;
import java.util.Queue;
/**
* @author yx
* @date 2023-04-08 12:04
*/
public class H1
static class Node implements Comparable<Node>
int count;
int color;
Node(int count, int color)
this.count = count;
this.color = color;
@Override
public int compareTo(Node o)
if(this.color==o.color)
return this.count-o.count;
else
return 0;
static PrintWriter out = new PrintWriter(System.out);
static BufferedReader ins = new BufferedReader(new InputStreamReader(System.in));
static StreamTokenizer in = new StreamTokenizer(ins);
public static void main(String[] args) throws IOException
String s = ins.readLine();
int n = Integer.parseInt(s);
String[] strings1 = ins.readLine().split(" ");
String[] strings2 = ins.readLine().split(" ");
Node[] nodes = new Node[n];
int count = 0;
int color = 0;
long ans=0;
ArrayList<Node>list=new ArrayList<>();
for (int i = 0; i < n; i++)
count = Integer.parseInt(strings1[i]);
color = Integer.parseInt(strings2[i]);
Node node = new Node(count, color);
list.add(node);
Collections.sort(list);
// for (int i = 0; i < n; i++)
// System.out.println(list.get(i).count);
//
// System.out.println(list.size());
int length=list.size();
for (int j = 0; j < length; j++)
for (int i = 1; i < list.size(); i++)
if (list.get(i).color == list.get(i - 1).color)
Node node1 = list.get(i);
Node node2 = list.get(i - 1);
Node node3 = new Node(0, 0);
if (node1.color == 0)
node3 = new Node(node1.count + node2.count, 1);
else if (node1.color == 1)
node3 = new Node(node1.count + node2.count, 2);
else
node3 = new Node(node1.count + node2.count, 0);
list.get(i-1).count = node3.count;
list.get(i-1).color = node3.color;
ans += node3.count;
list.remove(i);
// i--;
out.println(list.size()+" "+ans);
out.flush();
题目思路:
- 分堆问题,前两天刚做过,简单的分堆问题可以用优先队列,前天写的题解第四题合并果子但是很显然这题是加强版分堆问题,具体体现如下:
- 只有同一类的堆才能合并
- 堆合并之后会进化(堆号为0合并后--->堆号变为1........)
- 这题我用局部优先队列的思想,用ArrayList实现,自定义一个Node,然后重写排序,局部堆号相同的按堆数count递增排序(count小的先合,并保证count数大的堆重复合并次数最少)
- 从头节点开始往下遍历,判断下一个堆是否能合并,如果能合并,更新当前节点,删除下一个节点,ans+=当前节点的count+下一个节点的count
- 最后list的节点个数就是最小堆数
说在最后
趁着刚比完赛,思路还是比价清晰的,终于写完了题解,相比去年我感觉自己面对算法变得更加从容了一些(虽然还是算法小菜鸡),这段时间因为要备战考研,所以每天也就只能在上课的时候练算法题,考研之余写写算法有时会放松心情有时会增加焦虑,不管怎样,这一个月都坚持下来了,接下来就是安心备战考研啦,可能会很长一段时间不更文,各位uu尽情谅解⏲️
最后希望正在看这篇文章的uu,蓝桥都能取得好成绩!!!
蓝桥杯,咱们有缘江湖再见呀!

第十三届蓝桥杯大赛软件赛省赛 C/C++ 大学 B 组思考+总结
第十三届蓝桥杯大赛软件赛省赛 C/C++ 大学 B 组思考+总结
公告
第十三届蓝桥杯大赛软件赛省赛 C/C++ 大学 B 组
C题
刷题统计
D题
修剪灌木
E题
X进制减法
F题
统计子矩阵
G题
积木画
H题
扫雷
I题
李白打酒加强版
J题
砍竹子
注意事项:1. 对于编程题目,要求选手给出的解答完全符合 GNU C/C++ 标准,不能使用诸如绘图、Win32API、中断调用、硬件操作或与操作系统相关的 API。2. 代码中允许使用 STL 类库。3. main 函数结束必须返回 0。4. 所有依赖的函数必须明确地在源文件中 #include 5. 提交时,注意选择使用C或C++语言。
试题A: 九进制转十进制
本题总分:5分
【问题描述】
九进制正整数 (2022), 转换成十进制等于多少?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
题解:进制转换
2 * 9^0 + 2 * 9^1 + 0 + 2 * 9^3 = 1478
试题B: 顺子日期
本题总分:5分
【问题描述】
小明特别喜欢顺子。顺子指的就是连续的三个数字:123、456等。顺子日期指的就是在日期的 yyyymmdd 表示法中,存在任意连续的三位数是一个顺子的日期。例如20220123就是一个顺子日期,因为它出现了一个顺子: 123; 而20221023则不是一个顺子日期,它一个顺子也没有。小明想知道在整个2022年份中,一共有多少个顺子日期。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
题解:日历
很多人在讨论 012 算不算顺子,因为题目里说 0123 中的顺子是 123,我是算了的,不算的话答案应该是 4
年份 2022 是不变的,而且不可能搭上顺子,所以只考虑后四位即可
可能搭上顺子的月份有:
1月:0120 ~ 0129 共 10 个,顺子是 012 (其中 0123 可以认为顺子是 123)
10月:1012,顺子是 012
11月:1123,顺子是 123
12月:1230,1231,顺子是 123
一共 14 个
蓝桥杯2022年第十三届省赛真题-刷题统计
时间限制: 1s 内存限制: 256MB 提交: 8920 解决: 1735
题目描述
小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做 a 道题目,周六和周日每天做 b 道题目。请你帮小明计算,按照计划他将在第几天实现做题数大于等于 n 题?
输入格式
输入一行包含三个整数 a, b 和 n.
输出格式
输出一个整数代表天数。
样例输入
复制
10 20 99
样例输出
复制
8
提示
对于 50% 的评测用例,1 ≤ a, b, n ≤ 106 . 对于 100% 的评测用例,1 ≤ a, b, n ≤ 1018 .
80分解法:
#include<stdio.h>
long long int f(long long int n,long long int a,long long int b) //n代表总题数,a代表星期一到星期五做的题的数量,b代表星期六和星期天做题的数量
int flag;
long long int sum=0; //flag用来记录最后是在1-5停的,还是在6-7停的
while(n!=0)
n-=5*a; //先算1-5
if(n<0)
flag=1;
break;
sum+=5;
n-=2*b; //再算6-7
if(n<0)
flag=2;
break;
sum+=2;
if(flag==1) //如果是在1-5停的话
n+=5*a; //加回来,然后算是在第几天的
while(n>a)
n-=a;
sum++;
sum++; //不满一天就加回去
else if(flag==2)
n+=2*b;
while(n>b)
n-=b;
sum++;
sum++;
return sum;
int main()
long long int a,b,n;
scanf("%lld%lld%lld",&a,&b,&n);
printf("%lld",f(n,a,b));
return 0;
AC代码:
解题思路:
先用ans表示有多少周,n/(5*a+b*2)
工作日有二天,周末有二天
sum表示天数
用n-(5*a+2*b)*ans=剩余的天数
剩余的天数一定会落在工作日,或者周末这两种情况;
再用(n-(5*a+2*b)*ans)/a表示能在工作日完成的a题,
如果(n-(5*a+2*b)*ans)%a 不等于0,说明有剩余,还要加一天
在周末这种情况也同理;
注意事项:对于 100% 的评测用例,1 ≤ a, b, n ≤ 1018,要用long long
参考代码:
#include<bits/stdc++.h>
using namespace std;
int main()
long long a,b,n;
long long ans=0,sum=0;
scanf("%lld%lld%lld",&a,&b,&n);
ans+=n/(5*a+b*2);
sum=ans*7;
if((n-(a*5+b*2)*ans)<=5*a)
sum+=(n-(5*a+2*b)*ans)/a;
if((n-(5*a+2*b)*ans)%a!=0)
sum++;
else
sum+=5;
sum+=((n-(5*a+2*b)*ans)-5*a)/b;
if(((n-(5*a+2*b)*ans)-5*a)%b!=0)
sum++;
printf("%lld",sum);
题目 2657: 蓝桥杯2022年第十三届省赛真题-修剪灌木
时间限制: 1s 内存限制: 256MB 提交: 2361 解决: 1502
题目描述
爱丽丝要完成一项修剪灌木的工作。有 N 棵灌木整齐的从左到右排成一排。爱丽丝在每天傍晚会修剪一棵灌木,让灌木的高度变为 0 厘米。爱丽丝修剪灌木的顺序是从最左侧的灌木开始,每天向右修剪一棵灌木。当修剪了最右侧的灌木后,她会调转方向,下一天开始向左修剪灌木。直到修剪了最左的灌木后再次调转方向。然后如此循环往复。灌木每天从早上到傍晚会长高 1 厘米,而其余时间不会长高。在第一天的早晨,所有灌木的高度都是 0 厘米。爱丽丝想知道每棵灌木最高长到多高。
输入格式
一个正整数 N ,含义如题面所述。
输出格式
输出 N 行,每行一个整数,第i行表示从左到右第 i 棵树最高能长到多高。
样例输入
3
样例输出
4
2
4
提示
对于 30% 的数据,N ≤ 10. 对于 100% 的数据,1 < N ≤ 10000.
#include<stdio.h>
int main()
int n;
int a[10005];
scanf("%d",&n);
if(n%2==0)//n为偶数的时候
for(int i=1;i<=n/2;i++)
a[i]=2*(n-i);
printf("%d\\n",a[i]);
for(int j=n/2+1;j<=n;j++)
a[j]=a[n+1-j];
printf("%d\\n",a[j]);
if(n%2!=0)//n为奇数的时候
for(int i=1;i<=n/2;i++)
a[i]=2*(n-i);
printf("%d\\n",a[i]);
printf("%d\\n",n-1);
for(int j=n/2+2;j<=n;j++)
a[j]=a[n+1-j];
printf("%d\\n",a[j]);
return 0;
题目 2658: 蓝桥杯2022年第十三届省赛真题-X进制减法
时间限制: 1s 内存限制: 256MB 提交: 2258 解决: 651
题目描述
进制规定了数字在数位上逢几进一。
X 进制是一种很神奇的进制,因为其每一数位的进制并不固定!例如说某种 X 进制数,最低数位为二进制,第二数位为十进制,第三数位为八进制,则 X 进制数 321 转换为十进制数为 65。
现在有两个 X 进制表示的整数 A 和 B,但是其具体每一数位的进制还不确定,只知道 A 和 B 是同一进制规则,且每一数位最高为 N 进制,最低为二进制。请你算出 A − B 的结果最小可能是多少。
请注意,你需要保证 A 和 B 在 X 进制下都是合法的,即每一数位上的数字要小于其进制。
输入格式
第一行一个正整数 N,含义如题面所述。
第二行一个正整数 Ma,表示 X 进制数 A 的位数。
第三行 Ma 个用空格分开的整数,表示 X 进制数 A 按从高位到低位顺序各个数位上的数字在十进制下的表示。
第四行一个正整数 Mb,表示 X 进制数 B 的位数。
第五行 Mb 个用空格分开的整数,表示 X 进制数 B 按从高位到低位顺序各个数位上的数字在十进制下的表示。
请注意,输入中的所有数字都是十进制的。
输出格式
输出一行一个整数,表示 X 进制数 A − B 的结果的最小可能值转换为十进制后再模 1000000007 的结果。
样例输入
11
3
10 4 0
3
1 2 0
样例输出
94
提示
当进制为:最低位 2 进制,第二数位 5 进制,第三数位 11 进制时,减法得到的差最小。此时 A 在十进制下是 108,B 在十进制下是 14,差值是 94。
对于 30% 的数据,N ≤ 10; Ma, Mb ≤ 8. 对于 100% 的数据,2 ≤ N ≤ 1000; 1 ≤ Ma, Mb ≤ 100000; A ≥ B.
解题背景
1:理解进制的转化算法
2:理解如何达到最小值
注意:
1:如何是使得差值最小呢,我们可以利用dp的思想,要使得整体最小,那么组成他的各个部分也是最小,那么问题就变成了,如何使得各个部分的值最小;
2:每个部分有对应位上的差值组成,那么,要使得这个差值乘的进制数尽可能小就可以了;
3:如何使得进制尽可能小呢,进制的区间在2~N之间,那么只需要在这个区间之内,选取能包含a[i]和b[i]两个值的最小进制值就ok了,至此,思路就出来了
代码
#include<stdio.h>
int a[100005]=0;
int b[100005]=0;
int mod= 1000000007;
int max(int x,int y)
return x>y?x:y;
int main()
//录入数据
int N,Ma,Mb;
scanf("%d%d",&N,&Ma);
for(int i=Ma;i>=1;i--)
scanf("%d",&a[i]);
scanf("%d",&Mb);
for(int i=Mb;i>=1;i--)
scanf("%d",&b[i]);
//处理获取进制数组
int jz[100005]=0;
for(int i=Ma;i>=1;i--)//A-B以A 的位数为标准
jz[i]=max(max(a[i]+1,b[i]+1),2);//找出对应位置上最小的进位,且进位不小于2
//printf("%d ",jz[i]);
//printf("\\n");
/* //处理得到对应为的乘数 (超时O(n^2),换一种搞法)
int cs[100005]=0;
for(int i=Ma;i>=1;i--)
cs[i]=1;
for(int j=i-1;j>=1;j--)//乘数不包括自身进位值
cs[i]*=jz[j];
//printf("%d ",cs[i]);
//printf("\\n");
//处理得到最小值的和
int sum=0;
for(int i=Ma;i>=1;i--)//从高位加起
sum+=(a[i]-b[i])*cs[i];
sum%=mod;
*/
long long sum=0;
for(int i=Ma;i>=2;i--)
sum=((sum+a[i]-b[i])*jz[i-1])%mod;
sum+=(a[1]-b[1]);
printf("%lld\\n",sum);
return 0;
试题F: 统计子矩阵
时间限制:1.0s 内存限制: 256.0MB 本题总分:15分
【问题描述】
给定一个N×M的矩阵A,请你统计有多少个子矩阵(最小1×1,最大NxM)满足子矩阵中所有数的和不超过给定的整数K?
【输入格式】
第一行包含三个整数N,M和K.
之后N行每行包含M个整数,代表矩阵A.
【输出格式】
一个整数代表答案。
【样例输入】
3 4 10
1 2 3 4
5 6 7 8
9 10 11 12
1
2
3
4
【样例输出】
19
1
【样例说明】
满足条件的子矩阵一共有19,包含:
大小为1×1的有10个。
大小为1×2的有3个。
大小为1×3的有2个。
大小为1×4的有1个。
大小为2×1的有3个。
【评测用例规模与约定】
对于30%的数据, N, M ≤ 20.
对于70%的数据,N, M ≤ 100.
对于100%的数据,1 ≤ N,M ≤ 500; 0 ≤ Aij ≤1000;1 ≤ K ≤ 250000000.
题解:二维前缀和+二分
一看题就想到前缀和了,不过暴力枚举的话肯定超时了,想了个半枚举+二分查找的歪点子,时间复杂度大概 是O(n^3 * log(n)),大概有 10^9 了,再加上一点剪枝,能不能过看运气了
假设 (i, j) 是子矩阵的起点坐标,(x, y) 是终点坐标,枚举 i, j, x,二分查找符合条件的最大 y,就是找起点为 (i, j) ,终点在第 x 行最多有多少个矩阵
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MOD = 1000000007;
const int N = 505;
ll m, n, k;
ll a[N][N];
ll ans = 0;
ll getsum(int i, int j, int x, int y)
return a[x][y] - a[i - 1][y] - a[x][j - 1] + a[i - 1][j - 1];
int main()
cin >> m >> n >> k;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
cin >> a[i][j];
a[i][j] += a[i - 1][j] - a[i - 1][j - 1] + a[i][j - 1];
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
if (getsum(i, j, i, j) > k) continue;
for (int x = i; x <= m; x++)
int l = j, r = n;
while (l < r)
int mid = (l + r + 1) >> 1;
if (getsum(i, j, x, mid) > k) r = mid - 1;
else l = mid;
if (getsum(i, j, x, l) > k) break;
ans += l - j + 1;
cout << ans << endl;
return 0;
真·题解:前缀和 + 连续子段个数
这题有解了,其实是个套路题
先确定子矩阵的两个列边界,然后做一次行遍历,就是求符合条件的连续子段个数(双指针滑动窗口),复杂度缩小到 O(n^3)
由于每次只需拿到某一行内的和,只做一维前缀和即可
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll MOD = 1000000007;
const int N = 505;
ll m, n, k;
ll a[N][N];
ll ans = 0;
int main()
cin >> m >> n >> k;
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
cin >> a[i][j];
a[i][j] += a[i][j - 1];
for (int i = 1; i <= n; i++)
for (int j = i; j <= n; j++)
int left = 1;
ll cur = 0;
for (int right = 1; right <= m; right++)
cur += a[right][j] - a[right][i - 1];
while (cur > k)
cur -= a[left][j] - a[left][i - 1];
left++;
ans += right - left + 1;
cout << ans << endl;
return 0;
试题G: 积木画
时间限制: 1.0s 内存限制:256.0MB 本题总分:20分
【问题描述】
小明最近迷上了积木画,有这么两种类型的积木,分别为Ⅰ型(大小为2个单位面积)和L型(大小为3个单位面积):
同时,小明有一块面积大小为2×N的画布,画布由2×N个1×1区域构成。小明需要用以上两种积木将画布拼满,他想知道总共有多少种不同的方式? 积木可以任意旋转,且画布的方向固定。
【输入格式】
输入一个整数N,表示画布大小。
【输出格式】
输出一个整数表示答案。由于答案可能很大,所以输出其对1000000007取模后的值
【样例输入】
3
【样例输出】
5
【样例说明】
五种情况如下图所示,颜色只是为了标识不同的积木;
【评测用例规模与约定】
对于所有测试用例,1 ≤ N ≤ 10000000.
题解:动态规划(错解)
要摆出 n 列方格,可以在 n - 1 列方格后加一个竖着的 I 形积木,也可以在 n - 2 方格后加两个横着的 I 形积木,也可以在 n - 3 列方格上后加 两个 L 形积木的两种摆法
用 dp[i] 表示 i 列方格的摆法
则有,当 i >= 3 时 dp[i] = dp[i - 1] + dp[i - 2] + dp[i - 3] * 2;
以上是关于第十四届蓝桥杯大赛软件赛省赛JavaB组解析的主要内容,如果未能解决你的问题,请参考以下文章

 https://blog.csdn.net/m0_55858611/article/details/129960460?spm=1001.2014.3001.5501
https://blog.csdn.net/m0_55858611/article/details/129960460?spm=1001.2014.3001.5501