代码随想录|day38|动态规划part01● 理论基础 ● 509. 斐波那契数 ● 70. 爬楼梯 ● 746. 使用最小花费爬楼梯

Posted 2023-04-07 isabelightL

PS：贪心算法整一个大章节跳过了，过后两天补上。今天先跟上动态规划的步伐。

总链接：第九章 动态规划part01

动态规划基础

 打家劫舍3道，股票问题7、8道。

关键点：

1、找dp数组，下标的表示含义，一定要清楚dp[i][j]中i,j,的含义。

2、递推公式

3、dp数组如何初始化

4、遍历顺序

5、当自己感到迷惑时，要打印dp数组。

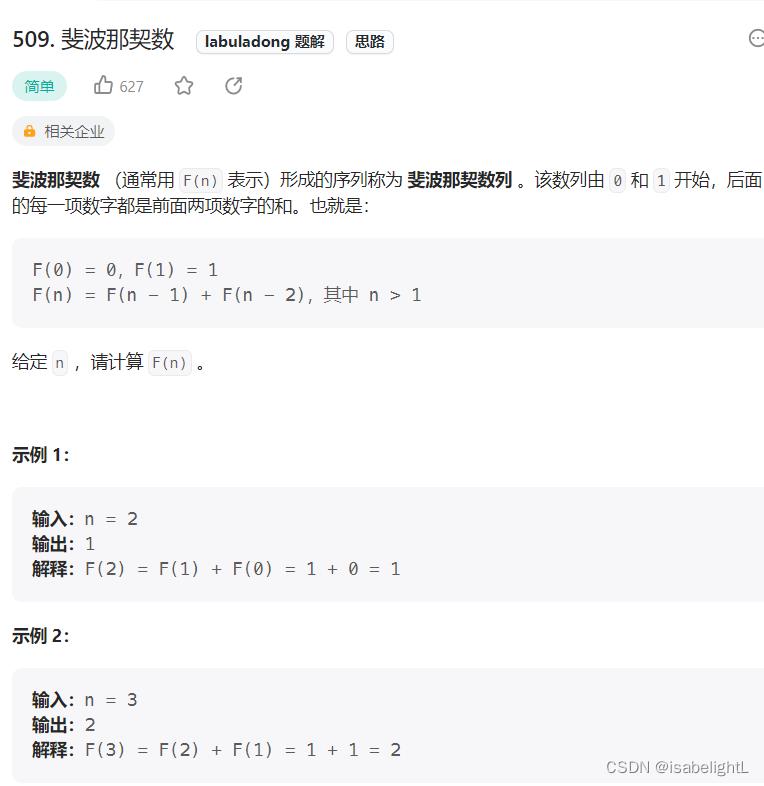
509. 斐波那契数

很简单的动规入门题，但简单题使用来掌握方法论的，还是要有动规五部曲来分析。

链接：代码随想录

自己的解法：

class Solution 
public:
    int fib(int n) 
        int a=0;
        int b=1;
        while(n>0)
        
            int temp=a;
            a=a+b;
            b=temp;
            n--;
        
        return a;

    
;

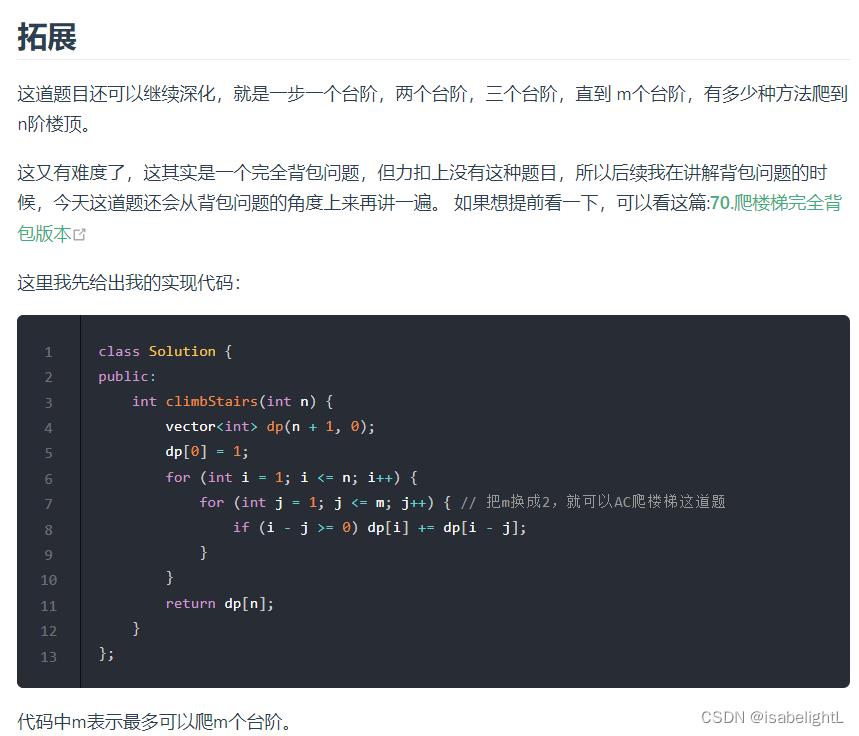
70. 爬楼梯

链接：代码随想录

 

class Solution 
public:
/*
    考虑最后一步
    dp[i] 代表到达第i节的爬法有dp[i]种，则：
    dp[i]=d[i-1]+dp[i-2]
 */
    int climbStairs(int n) 
        vector<int>dp(n+1,0);
        dp[0]=1;
        dp[1]=1;
        int i=2;
        while(i<=n)
        
            dp[i]=dp[i-1]+dp[i-2];
            i++;
        
        return dp[n];


    
;

 有拓展问题，但是没有看

 

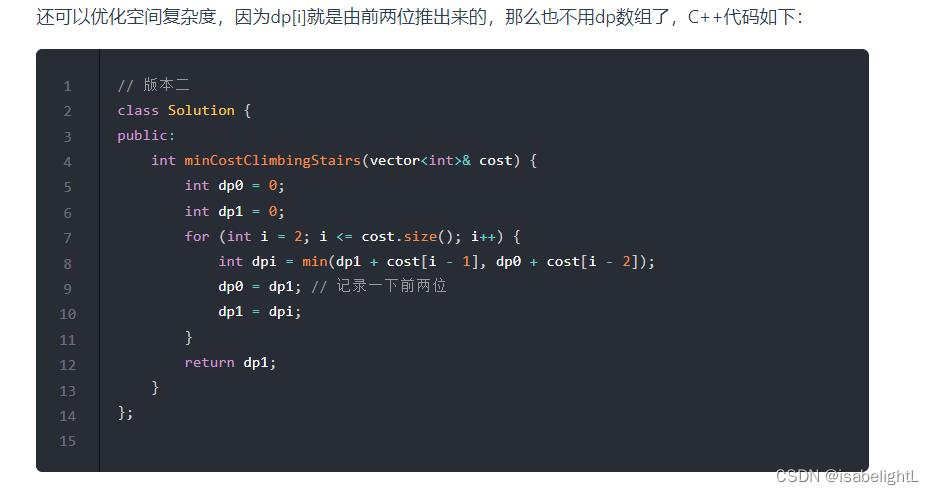
746. 使用最小花费爬楼梯

链接：代码随想录

 

 

class Solution 
/*
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
结合爬楼梯那道题来看，
*/
public:
    int minCostClimbingStairs(vector<int>& cost) 
        int n=cost.size();
        vector<int>dp(n+1,0);
        dp[0]=0;
        dp[1]=0;
        /*
        dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cos[i-2]);
        */
        for(int i=2;i<n+1;i++)
        
           dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]); 
        
        return dp[n];

        

    
;

 

 

LeetCode刷题笔记-动态规划-day7

文章目录

• LeetCode刷题笔记-动态规划-day7
• • 1014. 最佳观光组合
  • • 1.题目
    • 2.解题思路
    • 3.代码
  • 121. 买卖股票的最佳时机
  • • 1.题目
    • 2.解题思路
    • 3.代码
  • 122. 买卖股票的最佳时机 II
  • • 1.题目
    • 2.解题思路
    • 3.代码

LeetCode刷题笔记-动态规划-day7

1014. 最佳观光组合

1.题目

原题链接：1014. 最佳观光组合

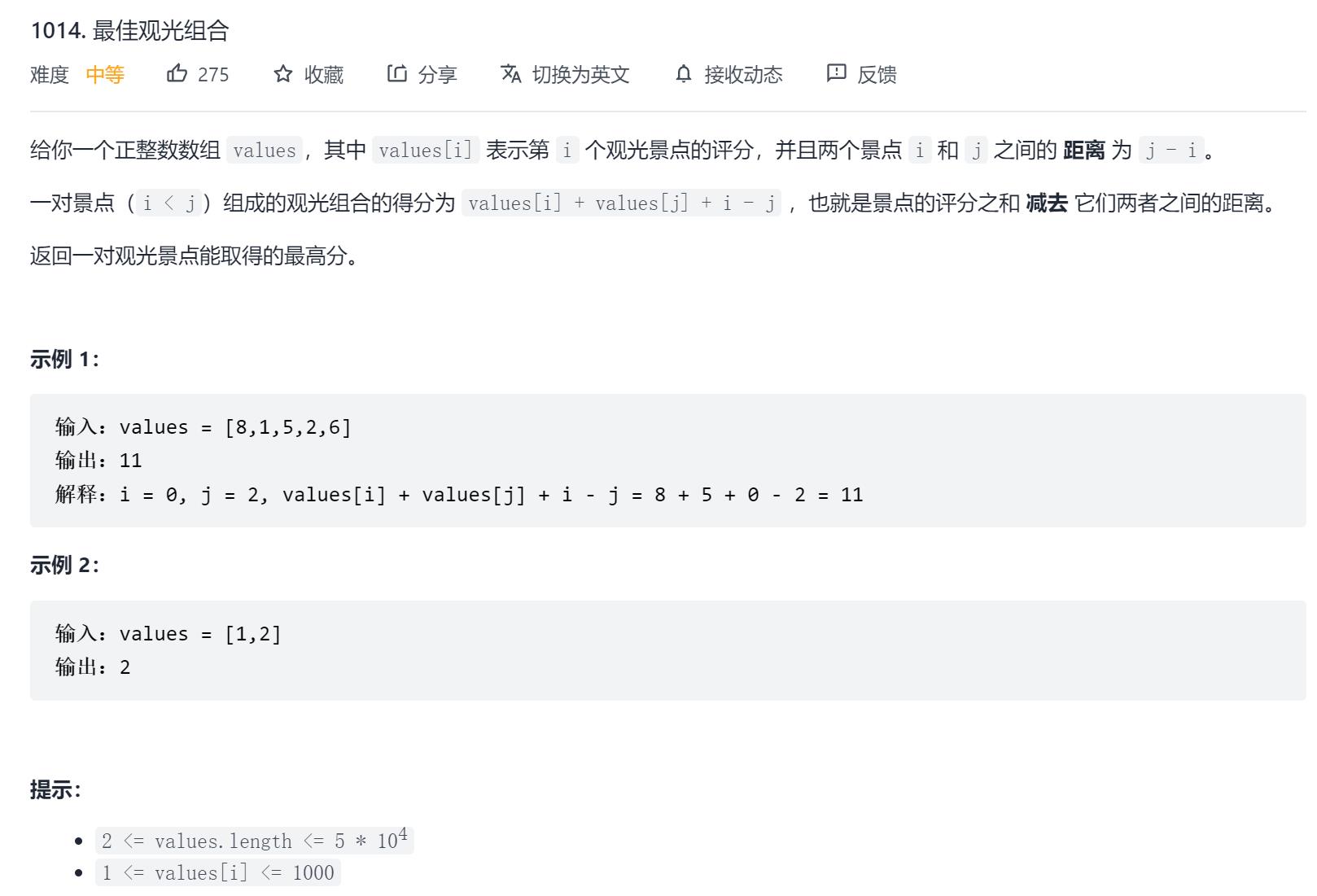
2.解题思路

1. 仔细观察a[i] + a[j] + i - j，可分解为：(a[j]-j)+(a[i]+i)
2. 又因为i<j，我们可以把j当做当前点，所以这道题我们只需要遍历一遍。用一个变量f维护j点之前的所有a[i]+i的最大值
3. res=max(res,f+a[j]-j);扫描一遍即可求出最大值

3.代码

class Solution 
public:
    int maxScoreSightseeingPair(vector<int>& a) 
        int f=a[0];
        int res=-1e9;
        for(int i=1;i<a.size();i++)
            res=max(res,f+a[i]-i);
            f=max(a[i]+i,f);
        
        return res;
    
;

121. 买卖股票的最佳时机

1.题目

原题链接：121. 买卖股票的最佳时机

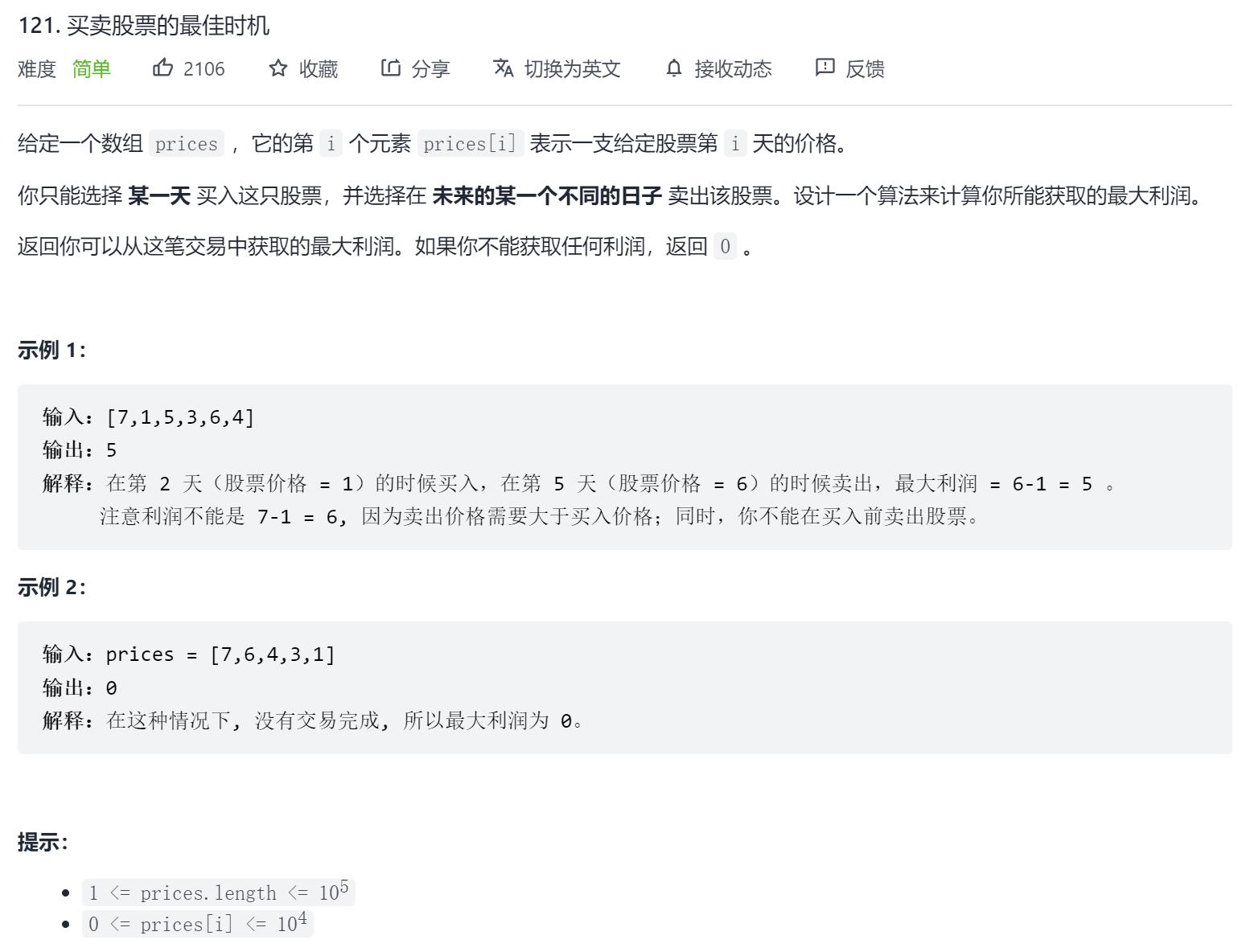
2.解题思路

1. 用一个变量minn维护[0,i-1]的最小价格
2. 枚举到i时，prices[i]-minn就表示当前点i卖出的最大收益
3. 遍历所有点，取最大值：res=max(res,prices[i]-minn);

3.代码

class Solution 
public:
    int maxProfit(vector<int>& prices) 
        int minn=1e9,res=0;
        for(int i=0;i<prices.size();i++)
            res=max(res,prices[i]-minn);
            minn=min(minn,prices[i]);
        
        return res;
    
;

122. 买卖股票的最佳时机 II

1.题目

原题链接：122. 买卖股票的最佳时机 II

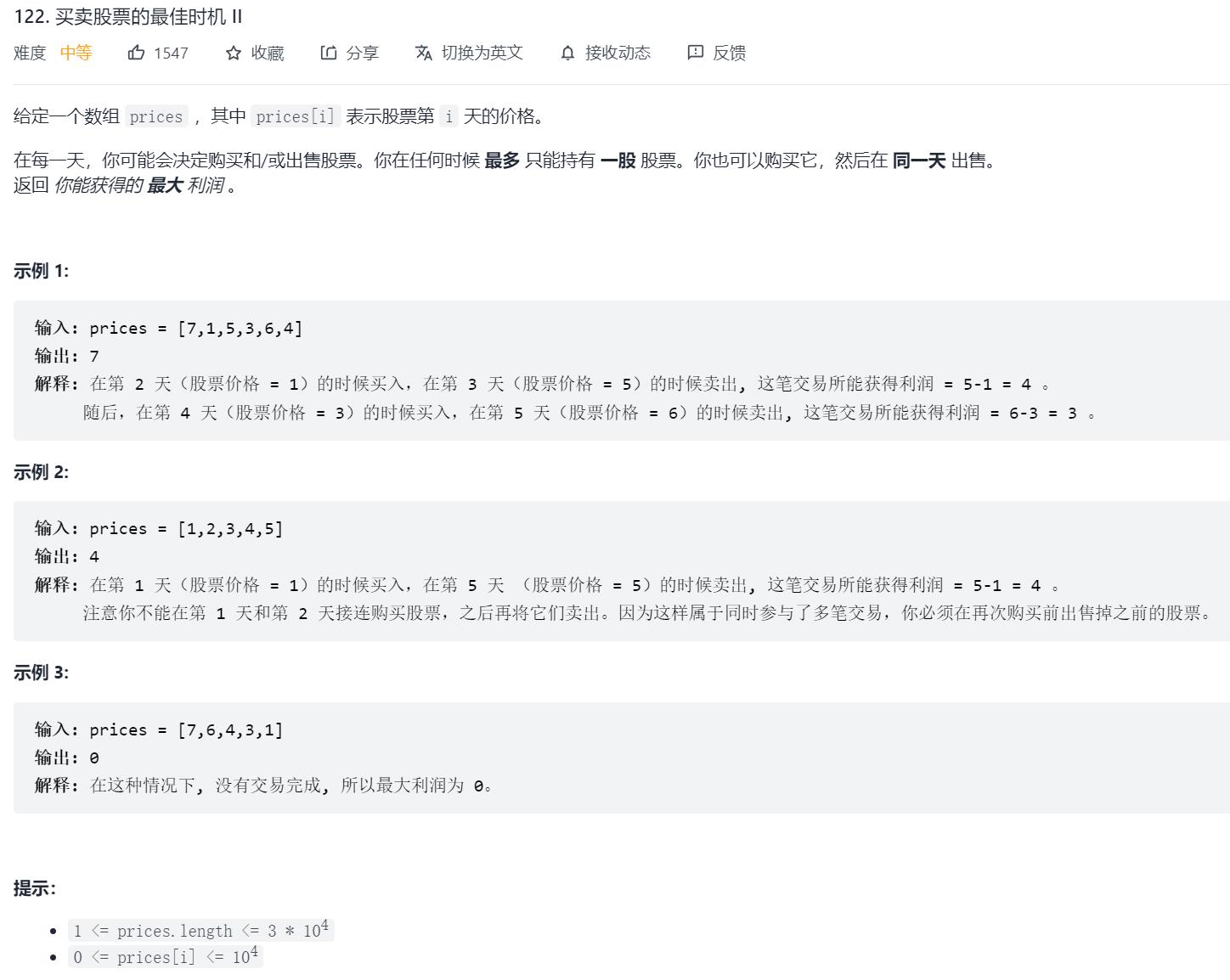
2.解题思路

算法：贪心

具体情况可以分为三类：

1. 单独交易日：设今天价格P1、明天价格P2，则今天买入、明天免除可赚取金额P2−P1(负值代表亏损)
2. 连续上涨交易日：设此上涨交易日股票价格分别为P1，P2，…，Pn 则第一天买最后一天卖收益最大，即Pn−P1；等价于每天都买卖，即Pn−P1=(P2−P1)+(P3−P2)+…+(Pn−Pn−1)
3. 连续下降交易日：则不买卖收益最大，即不会亏钱

总结可得到：由于不考虑交易次数。我们考虑相邻两天的股票价格，如果后一天的股票价格大于前一天的，那么在进行买入卖出操作后，即可获利。这样的贪心一定能获得最大的利润。

直接遍历整个数组。如果prices[i+1]-prices[i]大于0，则加入最终总利润。

3.代码

class Solution 
public:
    int maxProfit(vector<int>& prices) 
        int res=0;
        for(int i=0;i<prices.size()-1;i++)
            res+=max(0,prices[i+1]-prices[i]);
        
        return res;
    
;