Bezier Curve 贝塞尔曲线 - 在Unity中实现路径编辑

Posted 2023-04-06 CoderZ1010

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Bezier Curve 贝塞尔曲线 - 在Unity中实现路径编辑相关的知识，希望对你有一定的参考价值。

文章目录

简介
图形理解 Bezier Curve
应用

简介

贝塞尔曲线（Bezier Curve），又称贝兹曲线或贝济埃曲线，是计算机图形学中相当重要的参数曲线，在我们常用的软件如Photo Shop中就有贝塞尔曲线工具，本文简单介绍贝塞尔曲线在Unity中的实现与应用。

一阶贝塞尔曲线

给顶点P₀、P₁，只是一条两点之间的直线，公式如下：

B(t) = P₀ + (P₁ - P₀) t = (1 - t) P₀ + t P₁, t ∈ [0, 1]

等同于线性插值，代码实现如下：

/// <summary>
/// 一阶贝塞尔曲线
/// </summary>
/// <param name="p0">起点</param>
/// <param name="p1">终点</param>
/// <param name="t">[0,1]</param>
/// <returns></returns>
public static Vector3 Bezier1(Vector3 p0, Vector3 p1, float t)

    return (1 - t) * p0 + t * p1;

二阶贝塞尔曲线

路径由给定点P₀、P₁、P₂的函数计算，公式如下：

B(t) = (1 - t)² P₀ + 2t (1 - t) P₁ + t²P₂, t ∈[0, 1]

代码实现如下：

/// <summary>
/// 二阶贝塞尔曲线
/// </summary>
/// <param name="p0">起点</param>
/// <param name="p1">控制点</param>
/// <param name="p2">终点</param>
/// <param name="t">[0,1]</param>
/// <returns></returns>
public static Vector3 Bezier2(Vector3 p0, Vector3 p1, Vector3 p2, float t)

    Vector3 p0p1 = (1 - t) * p0 + t * p1;
    Vector3 p1p2 = (1 - t) * p1 + t * p2;
    return (1 - t) * p0p1 + t * p1p2;

三阶贝塞尔曲线

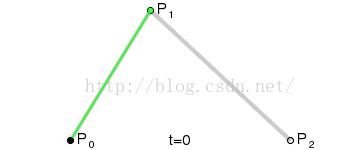
P₀、P₁、P₂、P₃四个点在平面或三维空间中定义了三次方贝塞尔曲线。曲线起始于P₀走向P₁，并从P₂的方向来到P₃，一般不会经过P₁、P₂，这两个点只是提供方向信息，可以将P₁、P₂理解为控制点。P₀和P₁之间的间距，决定了曲线在转而趋近P₃之前，走向P₂的长度有多长，公式如下：

B(t) = P₀(1 - t)³ + 3P₁t(1 - t)² + 3P₂t²(1 - t) + P₃t³, t ∈ [0, 1]

代码实现如下：

/// <summary>
/// 三阶贝塞尔曲线
/// </summary>
/// <param name="p0">起点</param>
/// <param name="p1">控制点1</param>
/// <param name="p2">控制点2</param>
/// <param name="p3">终点</param>
/// <param name="t">[0,1]</param>
/// <returns></returns>
public static Vector3 Bezier3(Vector3 p0, Vector3 p1, Vector3 p2, Vector3 p3, float t)

    Vector3 p0p1 = (1 - t) * p0 + t * p1;
    Vector3 p1p2 = (1 - t) * p1 + t * p2;
    Vector3 p2p3 = (1 - t) * p2 + t * p3;
    Vector3 p0p1p2 = (1 - t) * p0p1 + t * p1p2;
    Vector3 p1p2p3 = (1 - t) * p1p2 + t * p2p3;
    return (1 - t) * p0p1p2 + t * p1p2p3;

图形理解 Bezier Curve

使用Gizmos绘制Bezier Curve，通过图形理解贝塞尔曲线：

一阶贝塞尔曲线

P₀为起点，P₁为终点，t从0到1时，在贝塞尔曲线上对应的点为P_t，可以将t为理解为动画播放中的normalized time

一阶贝塞尔曲线

代码如下：

using UnityEngine;
using SK.Framework;

#if UNITY_EDITOR
using UnityEditor;
#endif

public class Example : MonoBehaviour

    private float t;

    private void Update()
    
        if (t < 1f)
        
            t += Time.deltaTime * .2f;
            t = Mathf.Clamp01(t);
        
    

#if UNITY_EDITOR
    private void OnDrawGizmos()
    
        Gizmos.color = Color.grey;
        Vector3 p0 = Vector3.left * 5f;
        Vector3 p1 = Vector3.right * 5f;
        Gizmos.DrawLine(p0, p1);
        Handles.Label(p0, "P0");
        Handles.Label(p1, "P1");
        Handles.SphereHandleCap(0, p0, Quaternion.identity, .1f, EventType.Repaint);
        Handles.SphereHandleCap(0, p1, Quaternion.identity, .1f, EventType.Repaint);
        Vector3 pt = BezierCurveUtility.Bezier1(p0, p1, t);
        Gizmos.color = Color.red;
        Gizmos.DrawLine(p0, pt);
        Handles.Label(pt, string.Format("Pt (t = 0)", t));
        Handles.SphereHandleCap(0, pt, Quaternion.identity, .1f, EventType.Repaint);
    
#endif

二阶贝塞尔曲线

P₀为起点，P₁为控制点，P₂为终点，t从0到1时，在贝塞尔曲线上对应的点为P_t

二阶贝塞尔曲线

代码如下：

using UnityEngine;
using SK.Framework;

#if UNITY_EDITOR
using UnityEditor;
#endif

public class Example : MonoBehaviour

    private float t;

    private void Update()
    
        if (t < 1f)
        
            t += Time.deltaTime * .2f;
            t = Mathf.Clamp01(t);
        
    

#if UNITY_EDITOR
    private void OnDrawGizmos()
    
        Gizmos.color = Color.grey;
        Vector3 p0 = Vector3.left * 5f;
        Vector3 p1 = Vector3.left * 2f + Vector3.forward * 2f;
        Vector3 p2 = Vector3.right * 5f;
        Gizmos.DrawLine(p0, p1);
        Gizmos.DrawLine(p2, p1);
        Handles.Label(p0, "P0");
        Handles.Label(p1, "P1");
        Handles.Label(p2, "P2");
        Handles.SphereHandleCap(0, p0, Quaternion.identity, .1f, EventType.Repaint);
        Handles.SphereHandleCap(0, p1, Quaternion.identity, .1f, EventType.Repaint);
        Handles.SphereHandleCap(0, p2, Quaternion.identity, .1f, EventType.Repaint);

        Gizmos.color = Color.green;
        for (int i = 0; i < 100; i++)
        
            Vector3 curr = BezierCurveUtility.Bezier2(p0, p1, p2, i / 100f);
            Vector3 next = BezierCurveUtility.Bezier2(p0, p1, p2, (i + 1) / 100f);
            Gizmos.color = t > (i / 100f) ? Color.red : Color.green;
            Gizmos.DrawLine(curr, next);
        
        Vector3 pt = BezierCurveUtility.Bezier2(p0, p1, p2, t);
        Handles.Label(pt, string.Format("Pt (t = 0)", t));
        Handles.SphereHandleCap(0, pt, Quaternion.identity, .1f, EventType.Repaint);
    
#endif

三阶贝塞尔曲线

P₀为起点，P₁为第一个控制点，P₂为第二个控制点，P₃为终点，t从0到1时，在贝塞尔曲线上对应的点为P_t

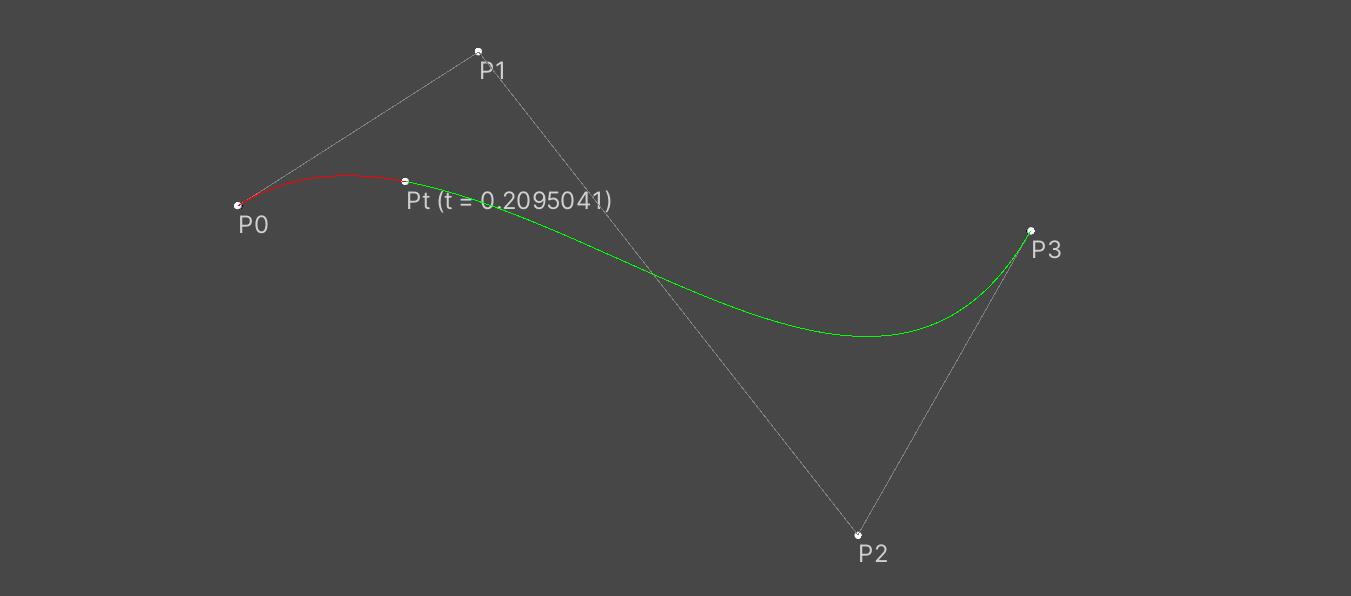
三阶贝塞尔曲线

代码如下：

using UnityEngine;
using SK.Framework;

#if UNITY_EDITOR
using UnityEditor;
#endif

public class Example : MonoBehaviour

    private float t;

    private void Update()
    
        if (t < 1f)
        
            t += Time.deltaTime * .2f;
            t = Mathf.Clamp01(t);
        
    

#if UNITY_EDITOR
    private void OnDrawGizmos()
    
        Gizmos.color = Color.grey;
        Vector3 p0 = Vector3.left * 5f;
        Vector3 p1 = Vector3.left * 2f + Vector3.forward * 2f;
        Vector3 p2 = Vector3.right * 3f + Vector3.back * 4f;
        Vector3 p3 = Vector3.right * 5f;
        Gizmos.DrawLine(p0, p1);
        Gizmos.DrawLine(p1, p2);
        Gizmos.DrawLine(p2, p3);
        Handles.Label(p0, "P0");
        Handles.Label(p1, "P1");
        Handles.Label(p2, "P2");
        Handles.Label(p3, "P3");
        Handles.SphereHandleCap(0, p0, Quaternion.identity, .1f, EventType.Repaint);
        Handles.SphereHandleCap(0, p1, Quaternion.identity, .1f, EventType.Repaint);
        Handles.SphereHandleCap(0, p2, Quaternion.identity, .1f, EventType.Repaint);
        Handles.SphereHandleCap(0, p3, Quaternion.identity, .1f, EventType.Repaint);

        Gizmos.color = Color.green;
        for (int i = 0; i < 100; i++)
        
            Vector3 curr = BezierCurveUtility.Bezier3(p0, p1, p2, p3, i / 100f);
            Vector3 next = BezierCurveUtility.Bezier3(p0, p1, p2, p3, (i + 1) / 100f);
            Gizmos.color = t > (i / 100f) ? Color.red : Color.green;
            Gizmos.DrawLine(curr, next);
        
        Vector3 pt = BezierCurveUtility.Bezier3(p0, p1, p2, p3, t);
        Handles.Label(pt, string.Format("Pt (t = 0)", t));
        Handles.SphereHandleCap(0, pt, Quaternion.identity, .1f, EventType.Repaint);
    
#endif

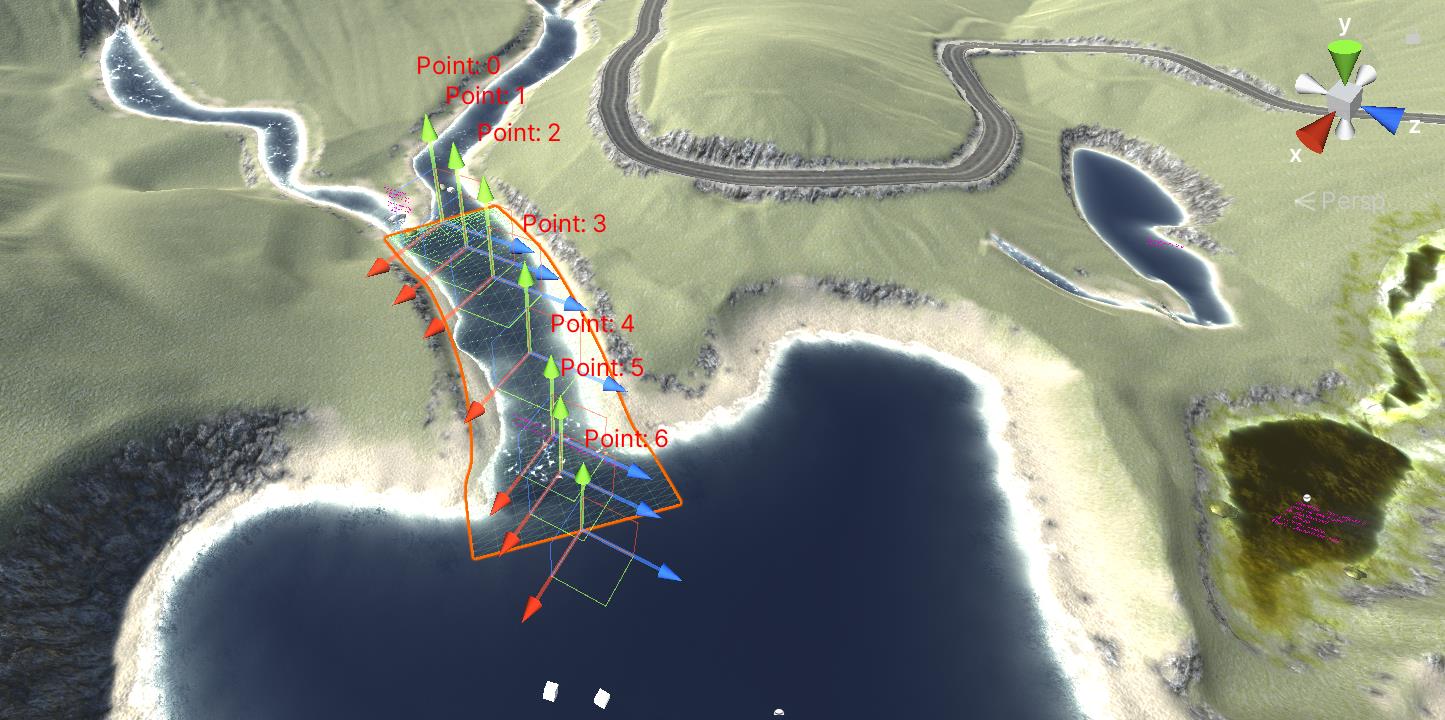
应用

常见的如道路编辑、河流编辑功能都可以通过贝塞尔曲线实现：

河流编辑

本文以一个简单的路径编辑为例，通过使用三阶贝塞尔曲线实现路径的编辑：

路径编辑

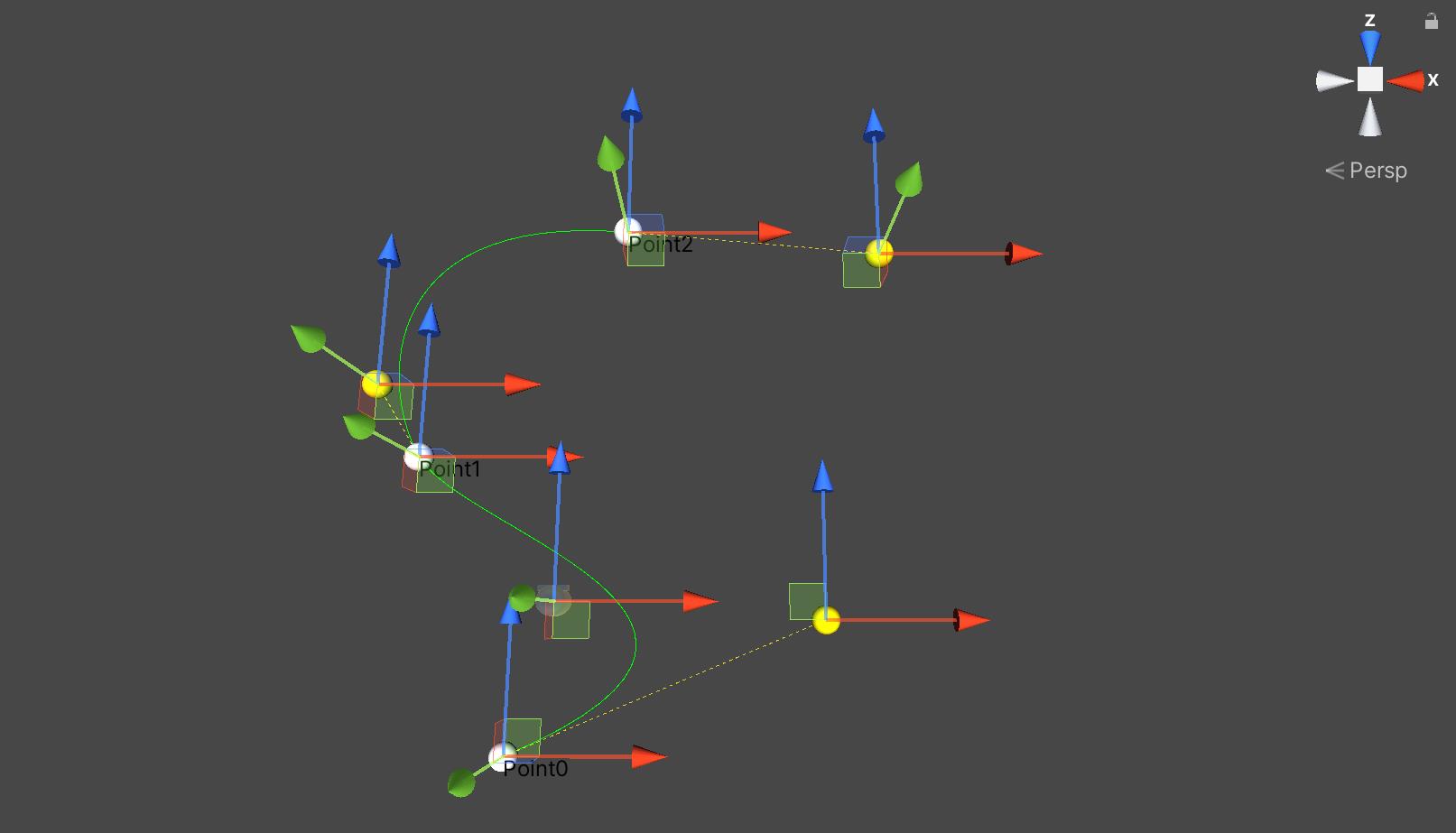
Bezier Curve

segments：贝塞尔曲线的段数，值越大曲线精度越高；
loop：是否循环（首尾相连）；
points ：点集合（结构体中包含坐标点和控制点）；

using System;
using UnityEngine;
using System.Collections.Generic;

namespace SK.Framework

    /// <summary>
    /// 贝塞尔曲线
    /// </summary>
    [Serializable]
    public class BezierCurve
    
        /// <summary>
        /// 段数
        /// </summary>
        [Range(1, 100)] public int segments = 10;

        /// <summary>
        /// 是否循环
        /// </summary>
        public bool loop;

        /// <summary>
        /// 点集合
        /// </summary>
        public List<BezierCurvePoint> points = new List<BezierCurvePoint>(2)
        
            new BezierCurvePoint()  position = Vector3.back * 5f, tangent = Vector3.back * 5f + Vector3.left * 3f ,
            new BezierCurvePoint()  position = Vector3.forward * 5f, tangent = Vector3.forward * 5f + Vector3.right * 3f 
        ;

        /// <summary>
        /// 根据归一化位置值获取对应的贝塞尔曲线上的点
        /// </summary>
        /// <param name="t">归一化位置值 [0,1]</param>
        /// <returns></returns>
        public Vector3 EvaluatePosition(float t)
        
            Vector3 retVal = Vector3.zero;
            if (points.Count > 0)
            
                float max = points.Count - 1 < 1 ? 0 : (loop ? points.Count : points.Count - 1);
                float standardized = (loop && max > 0) ? ((t %= max) + (t < 0 ? max : 0)) : Mathf.Clamp(t, 0, max);
                int rounded = Mathf.RoundToInt(standardized);
                int i1, i2;
                if (Mathf.Abs(standardized - rounded) < Mathf.Epsilon)
                    i1 = i2 = (rounded == points.Count) ? 0 : rounded;
                else
                
                    i1 = Mathf.FloorToInt(standardized);
                    if (i1 >= points.Count)
                    
                        standardized -= max;
                        i1 = 0;
                    
                    i2 = Mathf.CeilToInt(standardized);
                    i2 = i2 >= points.Count ? 0 : i2;
                
                retVal = i1 == i2 ? points[i1].position : BezierCurveUtility.Bezier3(points[i1].position,
                    points[i1].position + points[i1].tangent, points[i2].position
                    - points[i2].tangent, points[i2].position, standardized - i1);
            
            return retVal;

using System;
using UnityEngine;

namespace SK.Framework

    [Serializable]
    public struct BezierCurvePoint
    
        /// <summary>
        /// 坐标点
        /// </summary>
        public Vector3 position;

        /// <summary>
        /// 控制点 与坐标点形成切线
        /// </summary>
        public Vector3 tangent;

SimpleBezierCurvePath

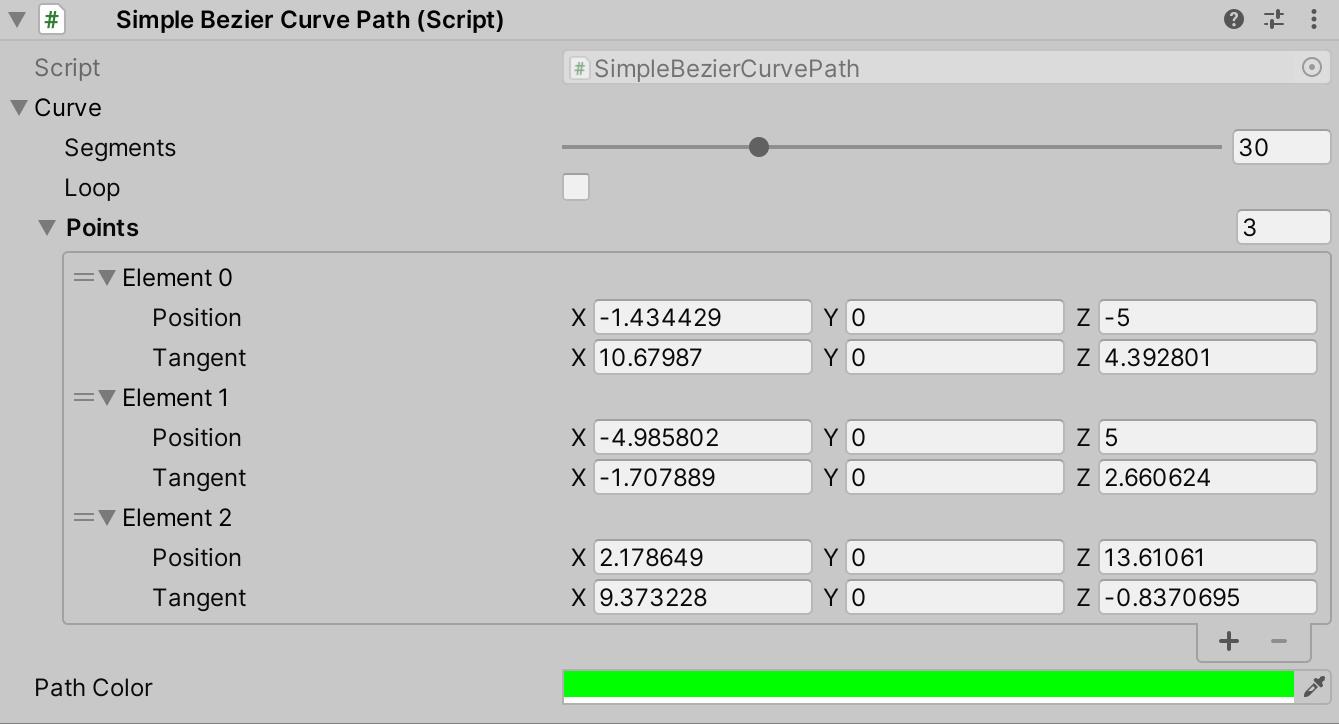
using UnityEngine;
using System.Collections.Generic;

#if UNITY_EDITOR
using UnityEditor;
#endif

namespace SK.Framework

    /// <summary>
    /// 贝塞尔曲线路径
    /// </summary>
    public class SimpleBezierCurvePath : MonoBehaviour
    
        [SerializeField] private BezierCurve curve;

        public bool Loop  get  return curve.loop;  

        public List<BezierCurvePoint> Points  get  return curve.points;  

        /// <summary>
        /// 根据归一化位置值获取对应的贝塞尔曲线上的点
        /// </summary>
        /// <param name="t">归一化位置值 [0,1]</param>
        /// <returns></returns>
        public Vector3 EvaluatePosition(float t)
        
            return curve.EvaluatePosition(t)Bezier曲线原理


贝塞尔曲线(Bézier curve)，又称贝兹曲线或贝济埃曲线，是应用于二维图形应用程序的数学曲线。一般的矢量图形软件通过它来精确画出曲线，贝兹曲线由线段与节点组成，节点是可拖动的支点，线段像可伸缩的皮筋，我们在绘图工具上看到的钢笔工具就是来做这种矢量曲线的。贝塞尔曲线是计算机图形学中相当重要的参数曲线，在一些比较成熟的位图软件中也有贝塞尔曲线工具，如PhotoShop等。在Flash4中还没有完整的曲线工具，而在Flash5里面已经提供出贝塞尔曲线工具。贝塞尔曲线于1962，由法国工程师皮埃尔·贝塞尔（Pierre
 Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau演算法开发，以稳定数值的方法求出贝兹曲线。
曲线作用
由于用计算机画图大部分时间是操作鼠标来掌握线条的路径，与手绘的感觉和效果有很大的差别。即使是一位精明的画师能轻松绘出各种图形，拿到鼠标想随心所欲的画图也不是一件容易的事。这一点是计算机万万不能代替手工的工作，所以到目前为止人们只能颇感无奈。使用贝塞尔工具画图很大程度上弥补了这一缺憾。贝塞尔曲线是计算机图形图像造型的基本工具，是图形造型运用得最多的基本线条之一。它通过控制曲线上的四个点（起始点、终止点以及两个相互分离的中间点）来创造、编辑图形。其中起重要作用的是位于曲线中央的控制线。这条线是虚拟的，中间与贝塞尔曲线交叉，两端是控制端点。移动两端的端点时贝塞尔曲线改变曲线的曲率（弯曲的程度）；移动中间点（也就是移动虚拟的控制线）时，贝塞尔曲线在起始点和终止点锁定的情况下做均匀移动。注意，贝塞尔曲线上的所有控制点、节点均可编辑。这种“智能化”的矢量线条为艺术家提供了一种理想的图形编辑与创造的工具。
公式

线性公式

给定点P0、P1，线性贝兹曲线只是一条两点之间的直线。且其等同于线性插值。这条线由下式给出：






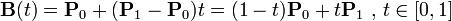
二次方公式


二次方贝兹曲线的路径由给定点P0、P1、P2的函数B（t）追踪：



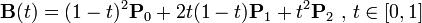
TrueType字型就运用了以贝兹样条组成的二次贝兹曲线。




三次方公式

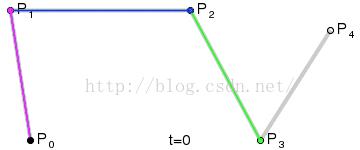
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝兹曲线。曲线起始于P0走向P1，并从P2的方向来到P3。一般不会经过P1或P2；这两个点只是在那里提供方向资讯。P0和P1之间的间距，决定了曲线在转而趋进P3之前，走向P2方向的“长度有多长”。


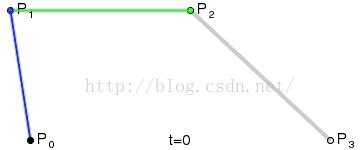
曲线的参数形式为：

 

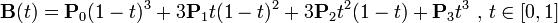
现代的成象系统，如PostScript、Asymptote和Metafont，运用了以贝兹样条组成的三次贝兹曲线，用来描绘曲线轮廓。




四次方图：






一般参数公式

阶贝兹曲线可如下推断。给定点P0、P1、…、Pn，其贝兹曲线即：





如上公式可如下递归表达： 用表示由点P0、P1、…、Pn所决定的贝兹曲线。

用平常话来说，阶的贝兹曲线，即双阶贝兹曲线之间的插值。




公式说明

1.开始于P0并结束于Pn的曲线，即所谓的端点插值法属性。

2.曲线是直线的充分必要条件是所有的控制点都位在曲线上。同样的，贝塞尔曲线是直线的充分必要条件是控制点共线。

3.曲线的起始点（结束点）相切于贝塞尔多边形的第一节（最后一节）。

4.一条曲线可在任意点切割成两条或任意多条子曲线，每一条子曲线仍是贝塞尔曲线。

5.一些看似简单的曲线（如圆）无法以贝塞尔曲线精确的描述，或分段成贝塞尔曲线（虽然当每个内部控制点对单位圆上的外部控制点水平或垂直的的距离为时，分成四段的贝兹曲线，可以小于千分之一的最大半径误差近似于圆）。

6.位于固定偏移量的曲线（来自给定的贝塞尔曲线），又称作偏移曲线（假平行于原来的曲线，如两条铁轨之间的偏移）无法以贝兹曲线精确的形成（某些琐屑实例除外）。无论如何，现存的启发法通常可为实际用途中给出近似值。










































以上是关于Bezier Curve 贝塞尔曲线 - 在Unity中实现路径编辑的主要内容，如果未能解决你的问题，请参考以下文章 
 贝塞尔曲线
 Bezier（贝塞尔）曲线简介
 bezier曲线的应用
 贝塞尔曲线实现的购物车添加商品动画效果
 Bezier曲线原理—动态解释
 cubic-bezier贝塞尔曲线css3动画工具