2022 第十三届蓝桥杯大赛软件赛省赛(第二场),C/C++ 大学B组题解
Posted 小哈里
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2022 第十三届蓝桥杯大赛软件赛省赛(第二场),C/C++ 大学B组题解相关的知识,希望对你有一定的参考价值。
2022 第十三届蓝桥杯大赛软件赛省赛(第二场),C/C++ 大学B组题解
文章目录
补题链接:地址
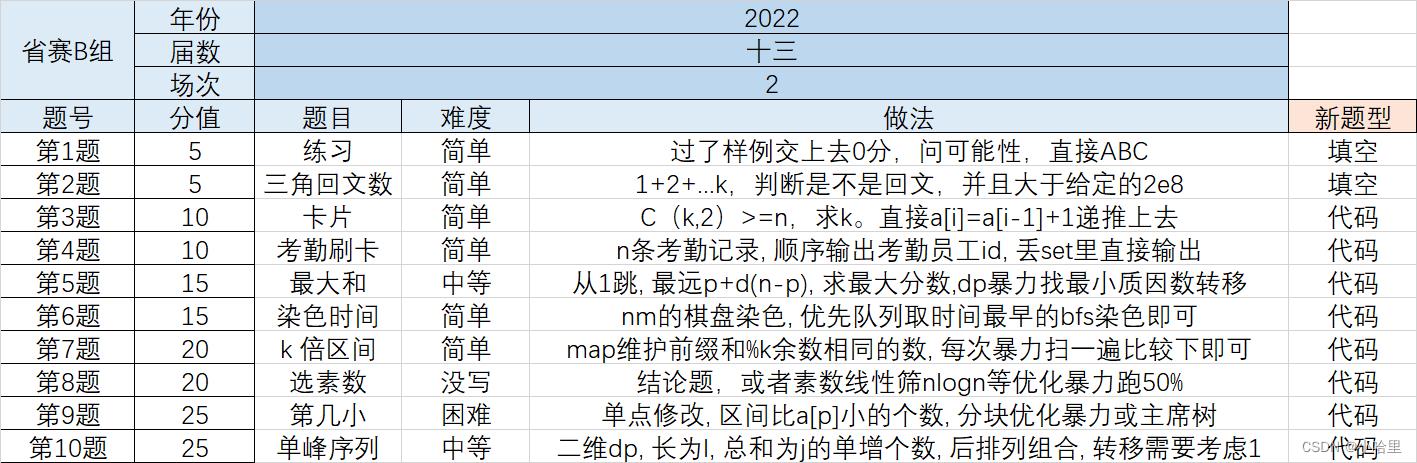
第1题 —— 练习 (5分)

- 题意:过了样例交上去0分,问可能是ABC的哪一种
- 显然都是,答案:ABC
#include <iostream>
using namespace std;
int main()
// 请在此输入您的代码
cout<<"ABC";
return 0;
第2题 —— 三角回文数 (5分)

-
题意:求第一个大于某2e8的数的回文数,且满足他可以等于1+2+…某个k。
-
一种是从2e8开始往上枚举,判断每个数是不是回文+三角,三角可以根号再乘附近的几个数特判一下。
另一种是枚举三角,1+2+…k,判断是不是回文和大于2e8,+k加到后面就是指数级了,上升也很快。 -
答案:35133153
#include<bits/stdc++.h>
using namespace std;
int main()
int x = 0;
for(int i = 1; ; i++)
x += i;
if(x <= 20220514)continue;
string s = to_string(x);
string t = s;
reverse(t.begin(),t.end());
if(s==t)break;
cout<<x<<"\\n";
return 0;
第3题 —— 卡片 (10分)

- 题意:n个人,给每个人随机发两张卡片(可以相同,没有顺序),求至少需要有多少种卡片,才能让n个人拿到的卡片组合都不同。
- 看一下样例,明显C(k,2)>=n,求k。(k-1)k/2>=n,可以跟上一题一样枚举,a[i]=a[i-1]+1递推上去即可。
#include<bits/stdc++.h>
using namespace std;
int main()
int n; cin>>n;
int i, x = 0;
for(i = 1; ; i++)
x += i;
if(x < n)continue;
break;
cout<<i<<"\\n";
return 0;
第4题 —— 考勤刷卡 (10分)


- 题意:n(1e4)条考勤记录,按顺序输出每个考勤了的员工的编号。
- 丢到set里输出就行,时间不用管。
#include<bits/stdc++.h>
using namespace std;
int main()
int n; cin>>n;
set<int>se;
for(int i = 1; i <= n; i++)
string t; int id; cin>>t>>id;
se.insert(id);
for(auto x : se)
cout<<x<<"\\n";
return 0;
第5题 —— 最大和 (15分)


- 题意:1-n共n个格子,每个格子有个分数(可能负数),开始站在1,下次可以跳到p+1到p+D(n-p)中的任意格子,D(x)为x的最小质因数,问能获得的最大分是多少。
- 数据范围n是1e4,感觉是个dp,状态到n为止能获得的最大分。 宝物绝对值不超过1e5,暴力转移的时候质因数分解logn(或者根号n直接暴力1e3最小质因数也可以的), nlogn刚好可以过。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1e5+10;
int a[maxn], f[maxn];
int isprime(int x) //判断素数
for(int i = 2; i*i <= x; i++)
if(x%i==0)return 0;
return 1;
int find(int x)//找最小质因数
if(x==0 || x==1)return x;
for(int i = 2; i*i <= x; i++)
if(x%i==0 && isprime(i))return i;
int main()
int n; cin>>n;
for(int i = 1; i <= n; i++)cin>>a[i];
memset(f, 0xc0, sizeof(f));
f[1] = a[1];
for(int i = 1; i <= n; i++)
int x = i+find(n-i); //最小质因数
for(int j = i+1; j <= x; j++)
f[j] = max(f[j], f[i]+a[j]);
cout<<f[n]<<"\\n";
return 0;
第6题 —— 染色时间 (15分)


- 题意:给出nm的棋盘,初始都是白色,每个格子被染色后等aij秒变色,变色后对四周的格子都染色,每个格子只能被染色一次。时刻0对a00染色,求多少时间染完棋盘。
- 感觉暴力bfs遍历就行,加个堆每次取出当前最早变色的格子出来给周围的染一下,然后维护下每个格子有没有都被染过就行。数据范围500可以说是随便怎么写都行了。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 510;
int a[maxn][maxn], vis[maxn][maxn];
struct nodeint x, y, time;; //完成变色的时间
bool operator < (node a, node b) return a.time > b.time;
priority_queue<node, vector<node>, less<node> >q;
int dx[] = 0,0,1,-1 ;
int dy[] = 1,-1,0,0 ;
int main()
int n, m; cin>>n>>m;
for(int i = 1; i <= n; i++)
for(int j = 1; j <= m; j++)
cin>>a[i][j];
int res = 0;
q.push((node)1, 1, a[1][1]);
vis[0][0] = 1;
while(q.size())
node t = q.top(); q.pop();
res = max(res, t.time);
for(int i = 0; i < 4; i++)
int nx = t.x+dx[i], ny = t.y+dy[i];
if(nx>=1&&nx<=n && ny>=1&&ny<=m && vis[nx][ny]==0)//没染过色
vis[nx][ny] = 1;
q.push((node)nx,ny, t.time+a[nx][ny]);
cout<<res<<"\\n";
return 0;
第7题 —— k 倍区间 (20分)

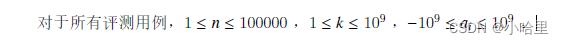
- 题意: 给出一个序列和一个k,求有多少个子区间的区间和是k的整数倍。
- 数据范围1e5,枚举所有区间是做不到了的, nlogn估计往数据结构去想,但是求子区间和无非也就是差分前缀和。
- 考虑前缀和求区间和,a[r]-a[l-1]是k的倍数,那么只要%k余数相同就好了,不难处理出过程中的前缀和值,然后前面有多少个跟当前%k余数相同的值,就是有多少个区间,扫一遍O(n)就行了(当然排序二分也是可以的,复杂度都一样,map查询logn,大家半斤八两)。
- 注意到一个坑点,不能是负整数倍,所以不能简单的累加,每次要遍历一遍%k余数的,要满足前面那个数比当前这个大才行。还有就是1e9的前缀和要开longlong。
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
map<int,vector<LL>>mp; //mp[x]: 维护余数为x的前缀和有哪些
LL s[4]; //前缀和, 滚动数组
int main()
int n, k; cin>>n>>k;
LL ans = 0;
mp[0].push_back(0); //别忘了
for(int i = 1; i <= n; i++)
int x; cin>>x;
s[i%2] = s[(i-1+2)%2]+x;
int r = (s[i%2]%k+k)%k; //%k余数
int len = mp[r].size();
for(int j = 0; j < len; j++)
if(mp[r][j] <= s[i%2])ans++;
// sort(mp[r].begin(), mp[r].end());
// ans += upper_bound(mp[r].begin(), mp[r].end(), s[i%2])-mp[r].begin();
mp[r].push_back(s[i%2]);
cout<<ans<<"\\n";
return 0;
第8题 —— 选素数 (20分)

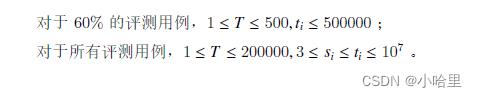
- 题意:给你两个数,s和t,每回合可以选一个小于s且不是s因数的素数p,然后找到p的倍数中刚好大于s的那个数y,并让s=y,进入下一回合。 求多少回合后s>t。
- 这题官网没有提交链接啊,代码补了对不对也不知道,我就不写了。。。(名正言顺的翘了摸鱼去了)
- 思路方向:
最大数据询问2e5,st 1e7,明显是个结论题, 可以找找规律。
20%的数据明显照着模拟就送。
50%数据500组,5e5,大概是优化下暴力,nlogn的复杂度,素数可以线性筛O(n)筛出来,个数大概是根号n,每次枚举每个素数,然后找倍数O1就够,如果满足条件就进入下一回合了,复杂度n根号n应该是可以拿到50%的。
或者,emmm,s-1,s-2这种很接近的数里应该有素数吧,并且肯定不是s的因数了,那么就O1过去了? 结论的话,盲猜跟gcd有点关系,不知道对不对,可以找找规律蛤。
第9题 —— 第几小 (25分)


- 题意:给一个数组,支持单点修改,以及求区间中比a[p]小的数的个数, a[p]在区间内。n是1e5,操作是2e5。
- 思路:首先,感觉暴力扫区间乱搞之类的可以拿40%。。1e5这种明显数据结构,区间操作就线段树。分块之类的应该也可以,一下子没想到线段树怎么维护,主席树第k小值应该可以做,感觉都有点长懒得写了,直接放一个可以过的分块代码
//分块可以AC 20个点的块长, sqrt(n)*5
#include<bits/stdc++.h>
using namespace std;
int main()
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n; cin>>n;
vector<int> a(n+1,0);
//分块
int len = sqrt(n)*5; //块长
int k = (n%len==0)?n/len:n/len+1;//块数
vector<int> block[k+1]; //本体
vector<int> belong(n+1,0);
int blockNum = 0;
for(int i=1;i<=n;i++) //分块
cin>>a[i];
blockNum=(i-1)/len+1;
belong[i]=blockNum;
block[blockNum].push_back(a[i]);
for(int i=1;i<=k;i++) //块排序
sort(block[i].begin(),block[i].end(),less<int>());
//输入操作
int m; cin>>m;
vector<vector<int>> op(m,vector<int>(4,0));
for(int i=0;i<m;i++)
cin>>op[i][0];
cin>>op[i][1]>>op[i][2];
if(op[i][0]==2)cin>>op[i][3];
//执行
vector<int> res;
for(int i = 0; i < m; i++)
int num1=op[i][1], num2=op[i][2], num3=op[i][3];
if(op[i][0]==1) //修改
auto it=lower_bound(block[belong[num1]].begin(),block[belong[num1]].end(),a[num1]);
block[belong[num1]].erase(it);
it=lower_bound(block[belong[num1]].begin(),block[belong[num1]].end(),num2);
if(it==block[belong[num1]].end())block[belong[num1]].push_back(num2);
else block[belong[num1]].insert(it,num2);
a[num1] = num2;
else //查询
int count = 0, mid = a[num3];
//先查左右两端分块中满足条件的元组数,因为num1和num2所在的块不一定一整块都参与比较
for(int j=num1;j<=min(num2,belong[num1]*len);j++)
if(a[j]<mid)count++;
if(belong[num1]!=belong[num2])
for(int j=(belong[num2]-1)*len+1;j<=num2;j++)
if(a[j]<mid)count++;
//区间查询,用二分法查询每个块中小于a[p]的元素个数
for(int j=belong[num1]+1;j<=belong[num2]-1;j++)
count+=lower_bound(block[j].begin(),block[j].end(),a[num3蓝桥杯 2022年省赛真题
C/C++ 大学B组
- 试题 A: 九进制转十进制
- 试题 B: 顺子日期
- 试题 C: 刷题统计
- 试题 D: 修剪灌木
- 试题 E: X 进制减法
- 试题 F: 统计子矩阵
- 试题 G: 积木画
- 试题 H: 扫雷
- 试题 I: 李白打酒加强版
- 试题 J: 砍竹子
虽然我的
J
a
v
a
\\mathrmJava
Java 组的,但怕被查重,等成绩公布了再做
J
a
v
a
\\mathrmJava
Java 的题解吧。
试题 A: 九进制转十进制
本题总分:
5
5
5 分
【问题描述】
九进制正整数
(
2022
)
9
(2022)_9
(2022)9 转换成十进制等于多少?
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
1478
#include <stdio.h>
int main()
int c, ans = 0;
while (c = getchar(), '0' <= c && c <= '9')
ans = ans * 9 + c - '0';
printf("%d", ans);
凭什么都是双非,
C
\\mathrm C
C 的签到难度这么低。
不公平不公平,重赛!重赛!
试题 B: 顺子日期
本题总分:
5
5
5 分
【问题描述】
小明特别喜欢顺子。顺子指的就是连续的三个数字
:
123
、
456
:123、456
:123、456 等。顺子日期指的就是在日期的
y
y
y
y
m
m
d
d
\\mathrmyyyymmdd
yyyymmdd 表示法中,存在任意连续的三位数是一个顺子的日期。例如
20220123
20220123
20220123 就是一个顺子日期,因为它出现了一个顺子:
123
123
123;而
20221023
20221023
20221023 则不是一个顺子日期,它一个顺子也没有。小明想知道在整个
2022
2022
2022 年份中,一共有多少个顺子日期。
【答案提交】
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
14
#include <stdio.h>
int year = 20220000, date, ans;
int days[13] = 0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31 , buff[8];
int main()
for (int month = 1; month <= 12; ++month)
for (int day = 1; day <= days[month]; ++day)
date = year + 100 * month + day;
for (int i = 0; i < 8; ++i)
buff[i] = date % 10, date /= 10;
for (int i = 1; i < 7; ++i)
if (buff[i] - buff[i + 1] == 1 &&
buff[i - 1] - buff[i] == 1)
++ans;
break;
printf("%d", ans);
虽然从题目描述中,无法直观的感受到所谓的顺子,是否包括如
321
321
321 这样递减的连续自然数列,但描述给出的样例
20221023
20221023
20221023 中包含了
210
210
210,基本上可以认为答案中不包含递减的连续自然数列的统计,但同时还有另一个问题,那就是顺子中能否包含
0
0
0。
总之,我认为是能包含
0
0
0 的,不愧是蓝桥,
题面做的真是有够失败的呢。
试题 C: 刷题统计
时间限制:
1.0
s
1.0\\mathrm s
1.0s 内存限制:
256.0
M
B
256.0\\mathrmMB
256.0MB 本题总分:
10
10
10 分
【问题描述】
小明决定从下周一开始努力刷题准备蓝桥杯竞赛。他计划周一至周五每天做
a
a
a 道题目,周六和周日每天做
b
b
b 道题目。请你帮小明计算,按照计划他将在第几天实现做题数大于等于
n
n
n 题?
【输入格式】
输入一行包含三个整数
a
,
b
a, b
a,b 和
n
n
n。
【输出格式】
输出一个整数代表天数。
【样例输入】
10 20 99
【样例输出】
8
【评测用例规模与约定】
对于
50
%
50\\%
50% 的评测用例,
1
≤
a
,
b
,
n
≤
1
0
6
1 ≤ a, b, n ≤ 10^6
1≤a,b,n≤106。
对于
100
%
100\\%
100% 的评测用例,
1
≤
a
,
b
,
n
≤
1
0
18
1 ≤ a, b, n ≤ 10^18
1≤a,b,n≤1018。
#include <stdio.h>
long long a, b, n, ans;
int main()
scanf("%lld %lld %lld", &a, &b, &n);
ans = n / (5 * a + 2 * b) * 7;
n %= 5 * a + 2 * b;
if (n > 5 * a)
ans += 5 + ((n - 5 * a) + b - 1) / b;
else
ans += (n + a - 1) / a;
printf("%lld", ans);
没啥好说的,
一个
a
/
b
a\\ /\\ b
a / b 向上取整的小技巧就是
(
a
+
b
−
1
)
/
b
(a + b - 1)\\ /\\ b
(a+b−1) / b 向下取整。
试题 D: 修剪灌木
时间限制:
1.0
s
1.0\\mathrm s
1.0s 内存限制:
256.0
M
B
256.0\\mathrmMB
256.0MB 本题总分:
10
10
10 分
【问题描述】
爱丽丝要完成一项修剪灌木的工作。
有
N
N
N 棵灌木整齐的从左到右排成一排。爱丽丝在每天傍晚会修剪一棵灌木,让灌木的高度变为
0
0
0 厘米。爱丽丝修剪灌木的顺序是从最左侧的灌木开始,每天向右修剪一棵灌木。当修剪了最右侧的灌木后,她会调转方向,下一天开始向左修剪灌木。直到修剪了最左的灌木后再次调转方向。然后如此循环往复。
灌木每天从早上到傍晚会长高 1 厘米,而其余时间不会长高。在第一天的早晨,所有灌木的高度都是
0
0
0 厘米。爱丽丝想知道每棵灌木最高长到多高。
【输入格式】
一个正整数
N
N
N ,含义如题面所述。
【输出格式】
输出
N
N
N 行,每行一个整数,第行表示从左到右第
i
i
i 棵树最高能长到多高。
【样例输入】
3
【样例输出】
4
2
4
【评测用例规模与约定】
对于
30
%
30\\%
30% 的数据,
N
≤
10
N ≤ 10
N≤10。
对于
100
%
100\\%
100% 的数据,
1
<
N
≤
10000
1 < N ≤ 10000
1<N≤10000。
#include <stdio.h>
int n;
int max(int a, int b) return a > b ? a : b;
int main()
scanf("%d", &n);
if (n == 1) putchar('1');
else for (int i = 1; i <= n; ++i)
printf("%d ", 2 * max(i - 1, n - i));
一颗灌木可以长到的最高高度,可能为:
1. 在它第一次被修剪之前
2. 它在某一次被修剪后,在此被修剪之前。
对于第二种情况,很容易分类出第
i
i
i 个灌木
t
i
t_i
ti 的最高高度为
max
2
×
(
i
−
1
)
,
2
×
(
n
−
i
)
\\max\\2 × (i - 1),2 × (n-i)\\
max2×(i−1),2×(n−i),即对应着爱丽丝从左端点折返和爱丽丝从右端点折返
t
i
t_i
ti 能达到的最高高度的取值。
同时
2
×
(
i
−
1
)
≤
i
2 × (i - 1) \\leq i
2×(i−1)≤i,仅在
i
≤
1
i \\leq 1
i≤1 成立,故对于第一种情况,无需额外的判断,直接取第二种情况的最大值即可。
试题 E: X 进制减法
时间限制:
1.0
s
1.0\\mathrm s
1.0s 内存限制:
256.0
M
B
256.0\\mathrmMB
256.0MB 本题总分:
15
15
15 分
【问题描述】
进制规定了数字在数位上逢几进一。
X
X
X 进制是一种很神奇的进制,因为其每一数位的进制并不固定!例如说某种
X
X
X 进制数,最低数位为二进制,第二数位为十进制,第三数位为八进制,则
X
X
X 进制数
321
321
321 转换为十进制数为
65
65
65。
现在有两个
X
X
X 进制表示的整数
A
A
A 和
B
B
B,但是其具体每一数位的进制还不确定,只知道
A
A
A 和
B
B
B 是同一进制规则,且每一数位最高为
N
N
N 进制,最低为二进制。请你算出
A
−
B
A − B
A−B 的结果最小可能是多少。
请注意,你需要保证
A
A
A 和
B
B
B 在
X
X
X 进制下都是合法的,即每一数位上的数字要小于其进制。
【输入格式】
第一行一个正整数
N
N
N,含义如题面所述。
第二行一个正整数
M
a
M_a
Ma,表示
X
X
X 进制数
A
A
A 的位数。
第三行
M
a
M_a
Ma 个用空格分开的整数,表示
X
X
X 进制数
A
A
A 按从高位到低位顺序各个数位上的数字在十进制下的表示。
第四行一个正整数