基于混合整数规划方法的微网电池储能容量优化配置

Posted 2023-04-06 程高兴

关键词：储能容量优化  储能配置  微网

相关参考资源：风电场风速两参数weibull(威布尔)分布的MATLAB小程序

风速威布尔分布和ARMA预测模型matlab程序

遗传算法优化神经网络，对光伏出力预测的优化设计，实现了部分功能

编程语言：matlab

主题：基于混合整数规划方法的微网电池储能容量优化配置

主要内容：

本代码目的为实现微电网内电池容量的优化配置，目标函数为配置过程中整体的运行成本最小或者经济效益最大化，约束条件则包括相应的运行约束以及能量平衡约束等等，最后将模型化简为一个混合整数线性规划问题，采用matlab对其进行高效求解。

部分结果截图：

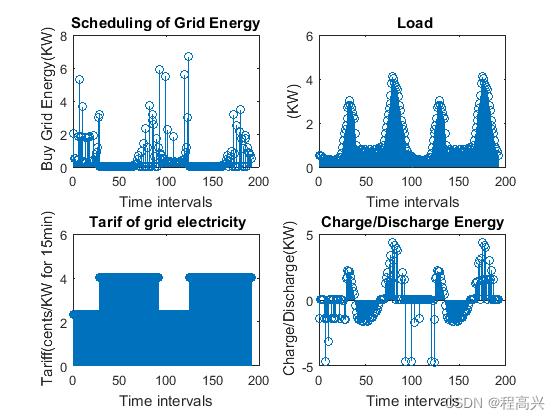
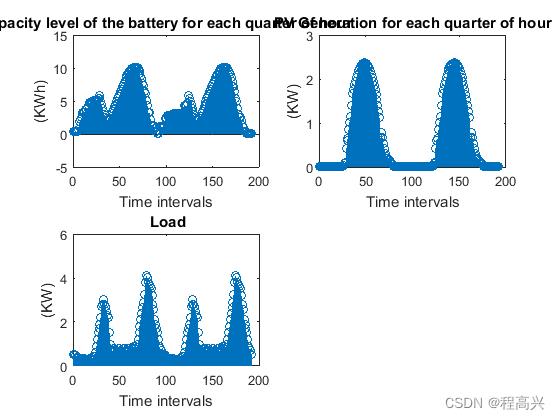
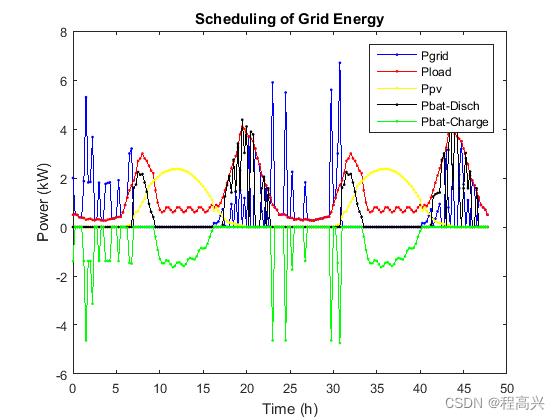
clear all;
clc;

%input data
% initial_capacity_battery=0; % KWh
% minimum_capacity_battery=0; %KWh
% maximum_capacity_battery=8; %KWh
% 
% max_batt_discharge=3;%KW
% max_batt_charge=3; %KW
% 
% battery_effic_disch=0.95; %it cant be 1. set 0.99
% battery_effic_charge=0.95; %it cant be 1. set 0.99

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%TESLA BATTERY
%input data
initial_capacity_battery=0; % KWh
minimum_capacity_battery=0; %KWh
maximum_capacity_battery=13.5; %KWh

max_batt_discharge=5;%KW
max_batt_charge=5; %KW

battery_effic_disch=0.95; %it cant be 1. set 0.99
battery_effic_charge=0.95; %it cant be 1. set 0.99

优化配置基于matlab两阶段鲁棒优化算法求解微网多电源容量配置优化问题含Matlab源码 2257期

⛄一、两阶段鲁棒优化算法求解微网多电源容量配置优化问题

1 微电网系统建模
图1所示为典型的微电网结构, 由可控分布式电源、可再生分布式电源、储能及本地负荷集成而成。此外, 考虑微电网内包含需求响应负荷的情况, 微电网可通过灵活调整需求响应负荷的用电计划, 降低运行成本。同时, 需求响应负荷也能通过提供该服务获取一定的收益。

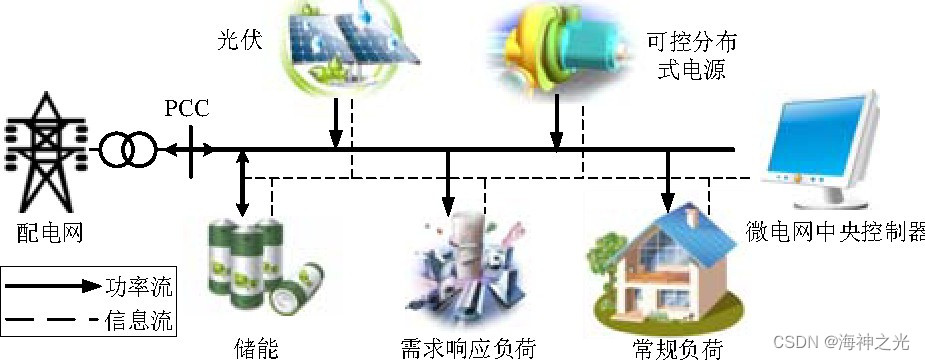
图1 微电网结构

在图1所示系统中, 微电网采用集中式控制结构, 由微电网中央控制器负责制定各单元第2日的运行计划, 所需的决策信息主要有:

1. 第2日可再生分布式电源出力和常规负荷功率的预测曲线;
2. 需求响应负荷的可调度范围、单位调度成本及期望用电计划;
3. 配电网日前交易电价及各时段与微电网交换功率的限值;
4. 储能单元和可控分布式电源的容量、调度功率限值及单位调度成本;
5. 储能单元的荷电状态限值及调度初始时刻的剩余容量。
   基于以上信息, 微电网中央控制器需综合考虑运行成本和风险, 得到经济性与可靠性兼顾的调度方案。

1.1 可控分布式电源
微电网中的可控分布式电源主要有微型燃气轮机、燃料电池等, 其发电成本可用线性函数表示。本文中考虑微电网内包含微型燃气轮机的情况, 其成本函数为

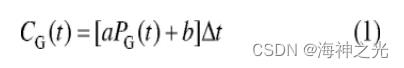
式中:CG (t) 表示微型燃气轮机在t时段的发电成本;a、b为成本系数;PG (t) 为t时段微型燃气轮机的输出功率;Δt为调度步长, 取值为1h。由于微型燃气轮机的功率响应速度相对于小时级调度而言较快, 因此不考虑其爬坡率约束, 仅考虑输出功率约束:

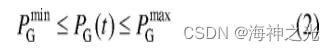
式中GPmax和GPmin表示微型燃气轮机的最大/最小输出功率, 分别受其额定功率和最小负载率的限制。

1.2 储能
储能的运行成本主要考虑其一次投资成本和运维成本[15], 在投资回收期内t时段的平均充放电成本CS (t) 可表示为

1.3 需求响应负荷
考虑微电网内包含可平移负荷的情况, 其在提供需求响应服务过程中的用电特性可用以下约束表示:

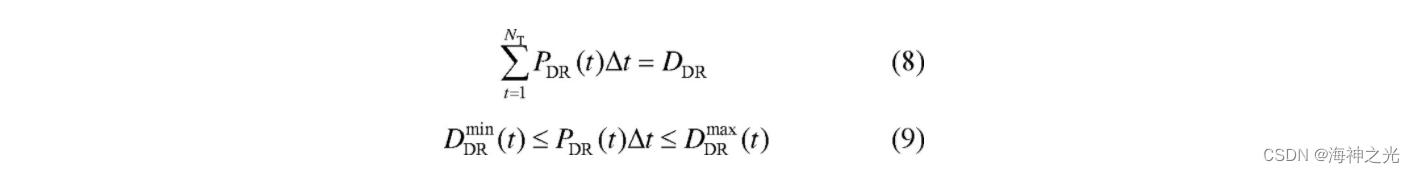
式中:PDR (t) 为t时段微电网对需求响应负荷的实际调度功率;DDR为需求响应负荷在调度周期内的总用电需求;DDRmax (t) 和DDRmin (t) 为需求响应负荷在t时段的最大/最小用电需求, 与用户对舒适度的要求有关。

在满足上述约束的基础上, 微电网可灵活调整需求响应负荷的用电计划。然而, 用电计划的改变势必影响用户的舒适度, 因此, 微电网需要给予适当的补偿, t时段所需付出的调度成本CDR (t) 可表示为

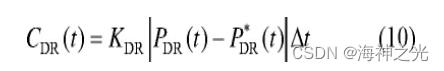
式中:KDR为需求响应负荷的单位调度成本;P*DR (t) 为t时段需求响应负荷的期望用电功率。式 (10) 中的绝对值项用于表示实际调度功率和期望用电功率之间的偏差, 通过引入辅助变量PDR1 (t) 、PDR2 (t) 及约束 (12) 、 (13) , 可将其化为式 (11) 所示的线性形式[17]:

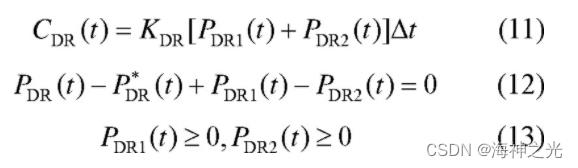
1.4 配电网交互功率
当微电网内各发电单元无法满足负荷需求时, 需要向配电网购电;反之, 微电网可将富余的电能出售给配电网, 获取收益。微电网和配电网之间的交互功率需满足如下平衡约束:

2 两阶段鲁棒优化模型
微电网的运行目标为日运行成本最小化, 如式 (18) 所示, 所需满足的约束条件包括式 (2) 、式 (4) — (9) 及式 (12) — (16) 。

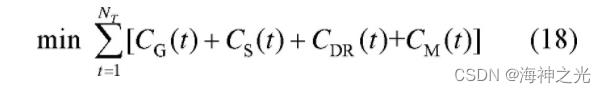
当不考虑光伏出力和负荷功率的不确定性时, 可得到上述微电网经济调度问题的确定性优化模型, 其紧凑形式可表述为

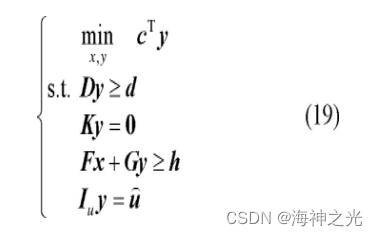
式中x、y为优化变量, 具体表达式为

上述模型为混合整数线性规划问题, 可采用常规的确定性优化方法进行求解[18], 得到的调度方案的最优性取决于预测的精度。然而, 微电网在实际运行中面临着诸多随机因素的影响, 预测精度难以保证。因此, 确定性优化模型得到的方案往往显得过于“冒险”, 需要在模型中计及不确定性的影响。考虑光伏出力和负荷功率的波动范围位于式 (22) 所构建的箱型不确定集U内:

本文搭建的两阶段鲁棒优化模型的目的在于找到不确定变量u在不确定集U内朝着最恶劣场景变化时经济性最优的调度方案, 具有如下形式:

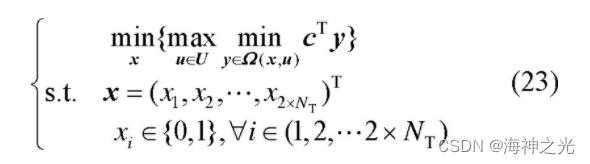
式中:外层的最小化为第一阶段问题, 优化变量为x;内层的最大最小化为第二阶段问题, 优化变量为u和y, 其中的最小化问题等同于式 (19) 的目标函数, 表示最小化运行成本;x和y的表达式如式 (20) 所示。Ω (x, u) 表示给定一组 (x, u) 时优化变量y的可行域, 具体表达式如下:

式中γ, λ, ν, π表示第二阶段的最小化问题中各约束对应的对偶变量。

对于每一组给定的不确定变量u, 式 (23) 都可以化简为式 (19) 所示的确定性优化模型, 而两阶段鲁棒模型第二阶段优化问题中max结构的目的就在于找到导致运行成本最大的最恶劣场景。

⛄二、部分源代码

clc
clear
close all
warning off
tic
%% 开始运行
%先运行一次，得到UB-LB
[yita,LB,ee_bat_int, p_wt_int,p_pv_int,p_g_int] = MP;
[p_wt,p_pv,p_load,x,UB] = SP(ee_bat_int,p_wt_int,p_pv_int,p_g_int,LB,yita);
UB1 = UB;
p(1)= UB - LB;
pub(1)=0;
plb(1)=0;
%开始迭代
for k=1:10
[yita,LB,ee_bat_int,p_wt_int,p_pv_int,p_g_int] = MP2(p_wt,p_pv,p_load);%MP迭代
[p_wt,p_pv,p_load,x,UB] = SP(ee_bat_int,p_wt_int,p_pv_int,p_g_int,LB,yita);%SP迭代
UB = min(UB1,UB);%取UB较小值
pub(k+1)=UB;
plb(k+1)=LB;
p(k+1) = UB-LB;
end
toc
%%绘图版块：主要绘制了各微网的日运行计划，容量配置结果，迭代过程等等
figure(1)
plot(x(1:24),‘-r*’)
xlim([1 24])
grid
hold on
plot(x(25:48),‘-b*’)
bar(x(49:72))
plot(x(73:96),‘-gd’)
plot(x(97:120),‘-md’)
title(‘典型日1场景下微网运行计划’)
legend(‘购电功率’,'售电功率 ',‘燃气轮机功率’,‘储能充电’,‘储能放电’)
xlabel(‘时间’)
ylabel(‘功率’)

figure(2)
plot(x(121:144),‘-r*’)
xlim([1 24])
grid
hold on
plot(x(145:168),‘-b*’)
bar(x(169:192))
plot(x(193:216),‘-g*’)
plot(x(217:240),‘-m*’)
title(‘典型日2场景下微网运行计划’)
legend(‘购电功率’,'售电功率 ',‘燃气轮机功率’,‘储能充电’,‘储能放电’)
xlabel(‘时间’)
ylabel(‘功率’)

figure(3)
plot(x(241:264),‘-r*’)
xlim([1 24])
grid
hold on
plot(x(265:288),‘-b*’)
bar(x(289:312))
plot(x(313:336),‘-g*’)
plot(x(337:360),‘-m*’)
title(‘典型日3场景下微网运行计划’)
legend(‘购电功率’,'售电功率 ',‘燃气轮机功率’,‘储能充电’,‘储能放电’)
xlabel(‘时间’)
ylabel(‘功率’)

figure(4)
plot(x(361:384),‘-r*’)
xlim([1 24])
grid
hold on
plot(x(385:408),‘-b*’)
bar(x(409:432))
plot(x(433:456),‘-g*’)
plot(x(457:480),‘-m*’)
title(‘典型日4场景下微网运行计划’)
legend(‘购电功率’,'售电功率 ',‘燃气轮机功率’,‘储能充电’,‘储能放电’)
xlabel(‘时间’)
ylabel(‘功率’)

% figure(1)
% bar(R_31);
% set(gca,‘XTickLabel’,‘A’,‘B’,‘C’);
% for i=1:3
% text(i,R_31(i)+0.03,num2str(R_31(i)),‘VerticalAlignment’,‘bottom’,‘HorizontalAlignment’,‘center’);%就是用test加数值，这个0.03看情况定，根据数值大小，再改就好了
% end
% ylim([0,1.2]);
% ylabel(‘R^2’);

figure(5)
bar([ee_bat_int,p_g_int,p_pv_int,p_wt_int],0.5);
set(gca,‘XTickLabel’,‘储能容量’,‘燃气轮机容量’,‘光伏容量’,‘风机容量’);
ylim([0,620]);
ylabel(‘配置结果’);

figure(6)
[ss,gg]=meshgrid(1:4,1:24 );
plot3(ss,gg,p_load,‘-’);
xlabel(‘微网编号’);
ylabel(‘时刻’);
zlabel(‘负荷值’);
title(‘负荷调度结果图’);
legend(‘负荷曲线1’,'负荷曲线2 ','负荷曲线3 ','负荷曲线4 ')

figure(7)
[ss,gg]=meshgrid(1:4,1:24 );
plot3(ss,gg,p_pv,‘-’);
xlabel(‘微网编号’);
ylabel(‘时刻’);
zlabel(‘光伏出力’);
title(‘光伏调度结果图’);
legend(‘光伏曲线1’,'光伏曲线2 ','光伏曲线3 ','光伏曲线4 ')

figure(8)
[ss,gg]=meshgrid(1:4,1:24 );
mesh(ss,gg,p_wt);
xlabel(‘微网编号’);
ylabel(‘时刻’);
zlabel(‘风机出力’);
title(‘风机调度结果图’);
legend(‘风机曲线1’,'风机曲线2 ','风机曲线3 ','风机曲线4 ')

figure(9)
plot(pub(1:10),‘-‘)
hold on
plot(plb(1:10),’-’)
xlabel(‘迭代次数’)
ylabel(‘数值’)
legend(‘上界限曲线’,'下界限曲线 ')
title(‘运行曲线’)

figure(10)
plot(p(1:10))
xlabel(‘迭代次数’)
ylabel(‘UB-LB’)
title(‘运行曲线’)

⛄三、运行结果

⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]刘一欣,郭力,王成山.微电网两阶段鲁棒优化经济调度方法[J].中国电机工程学报. 2018,38(14)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除