多微电网计及碳排放的基于交替方向乘子法（ADMM）的多微网电能交互分布式运行策略研究（Matlab代码实现）

Posted 2023-04-06 我爱Matlab编程

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

---

💥1 概述

随着全球能源与环境问题日渐严峻，风能、光能等可再生清洁能源的有效利用意义重大。微电

网作为新兴能源的主要载体，它的研究有助于人们应对能源与环境的双重危机。目前微电网技术

的主要研究课题是妥善管理微电网内分布式电源和储能装置的运行。通过建立微电网优化数学模

型，在满足系统负载需求和外部约束下，使用数学 方法或人工智能算法来求解得出最合理的调度方 案，进而达到充分利用可再生能源，实现微电网经济效益和环境效益最大化的目的［1］。目前，国内外对微电网优化调度方面的研究成果颇丰。文献［2］为了解决传统智能算法在求

解微电网多目标函数时易早熟、陷入局部最优、收敛速度和精度差等问题，建立以运行成本、环境污染处理费用为目标的优化模型，用改进的鸟群算法对该模型进行求解，验证了所建模型和改进算

法的有效性。文献［3］对含有光伏、风机、柴油发电机以及铅酸蓄电池组成的孤立微电网进行研

究，提出了一种经济与环保协调控制下的微电网优化调度模型。文献［4］在多目标遗传算法中引

入初始点引导技术和去重操作，并将其应用于微电网双目标优化模型，得到较均匀的 Pareto 前沿，证实了所提出的方法的有效性。文献［5］基于交替方向乘子法，用分散式优化方法来解决微电网的动态经济调度问题，解决了集中式优化调度所面临的种种难题。通过对几个系统进行计算，表明所提方法具有良好的收敛特性以及较快的收敛速度。文献[6］通过建立主从博弈模型来解决交

直流混合微网运行中光伏消纳率和综合网损率的问题。该模型满足综合网损率指标的同时，还最

小化运行成本，最大化光伏消纳率，保证了交直流混合微网的综合效益。

交替方向乘子法非常适用于大规模分布式计算系统[19-20] ，由于不需要将微电网信息进行集中计算，而是各微电网自行求解目标函数后，根据多微电网系统层面的约束条件进行乘子的更新与迭代，其在满足各微电网运行成本最小的同时也实现了整个系统的能量平衡；此外，在各微电网能量管理系统进行计算的方式也能充分保护微电网的隐私。在假定通信通道是理想可靠的前提下，本文对计及碳排放的基于交替方向乘子法（ADMM）的多微网电能交互分布式运行策略进行研究。

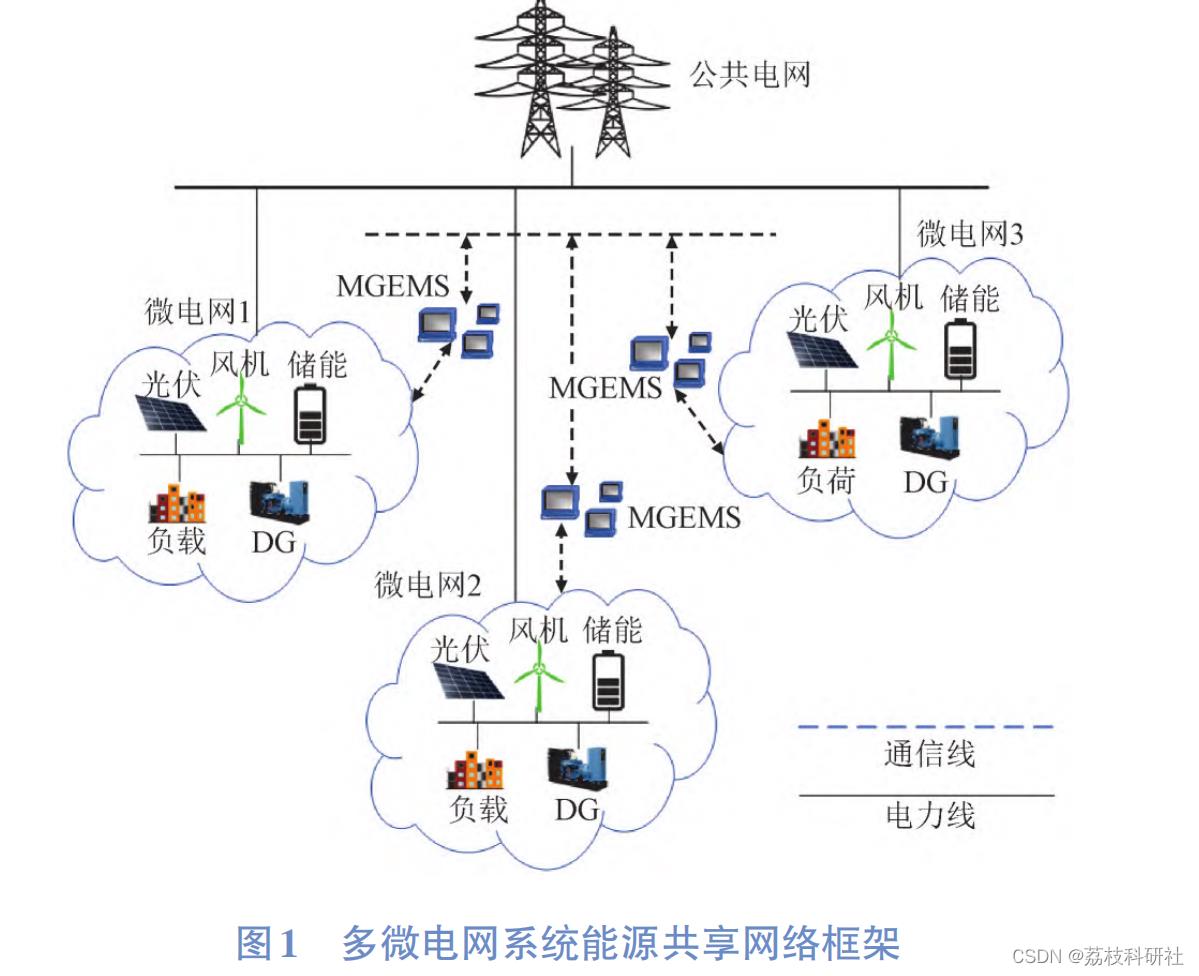
对于分布式优化问题,交替方向乘子法(ADMM)属于一种简单高效、鲁棒性强的算法,其具有良好收敛性的同时,不要求优化问题的目标函数为严格的凸函数。

ADMM 融合了对偶上升法的可分解性以及乘子法较好的收敛性，核心思想是将一个大的问题

分解成若干个小问题，交替迭代进行求解，使原目标与其对偶变量共同收敛。其 标 准 形 式 如

下:

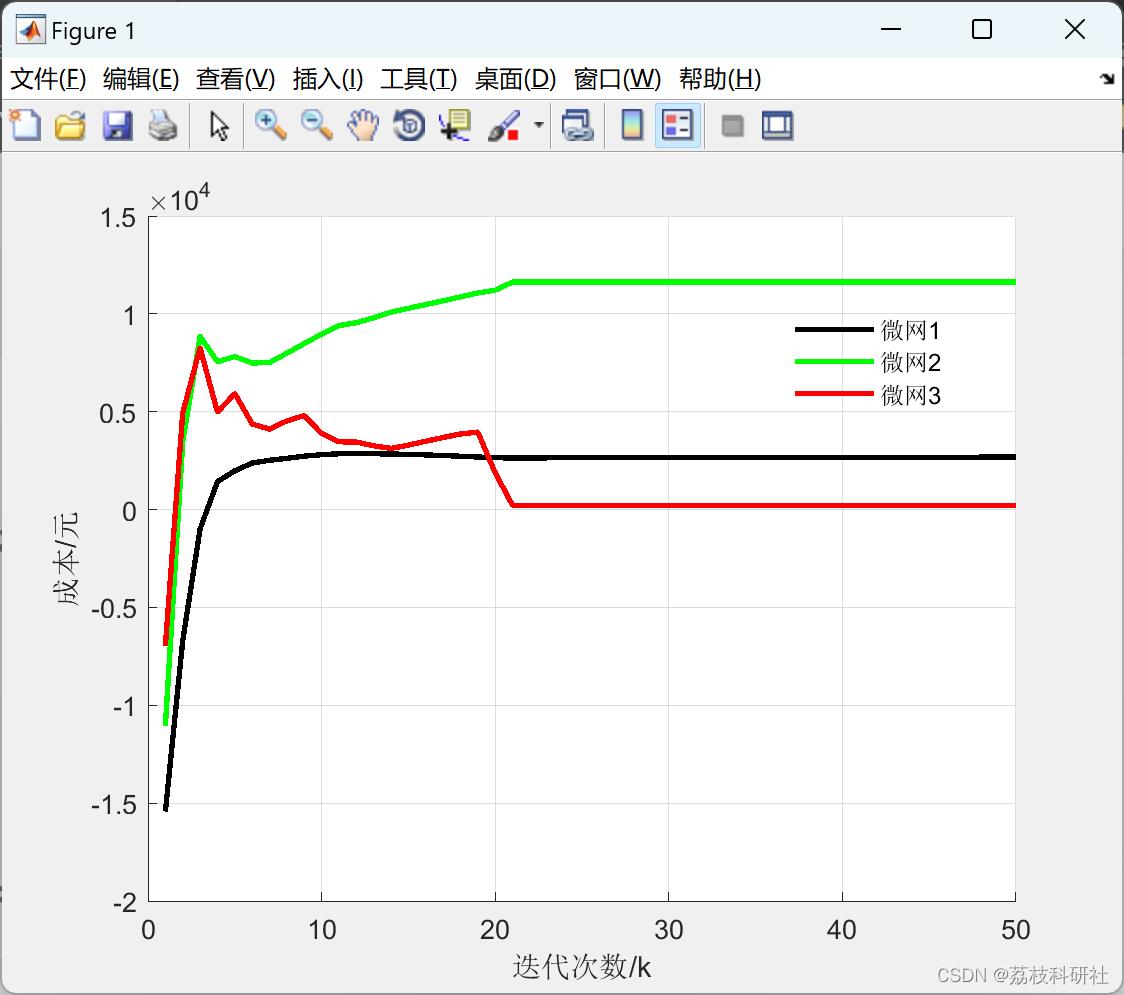
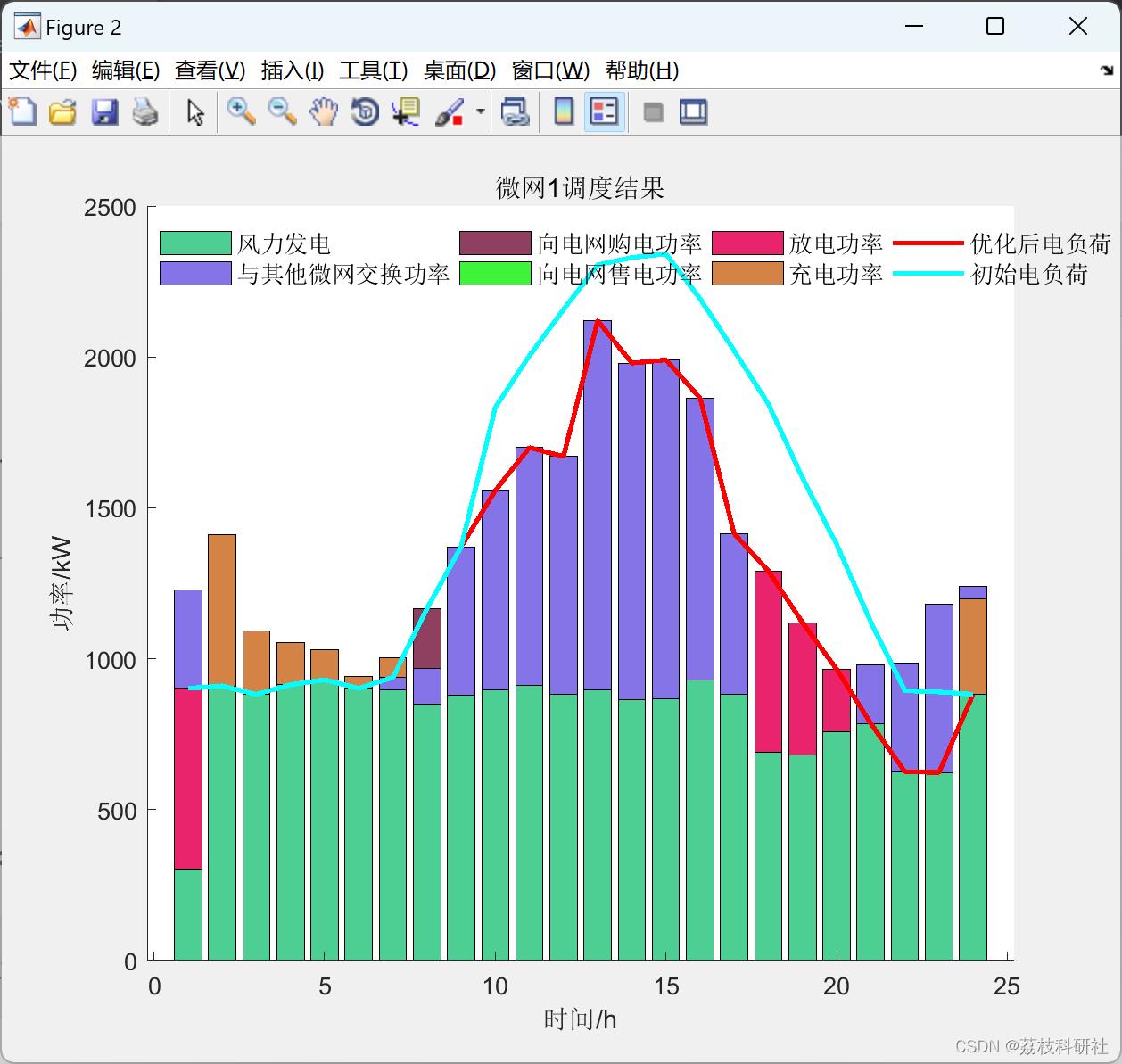
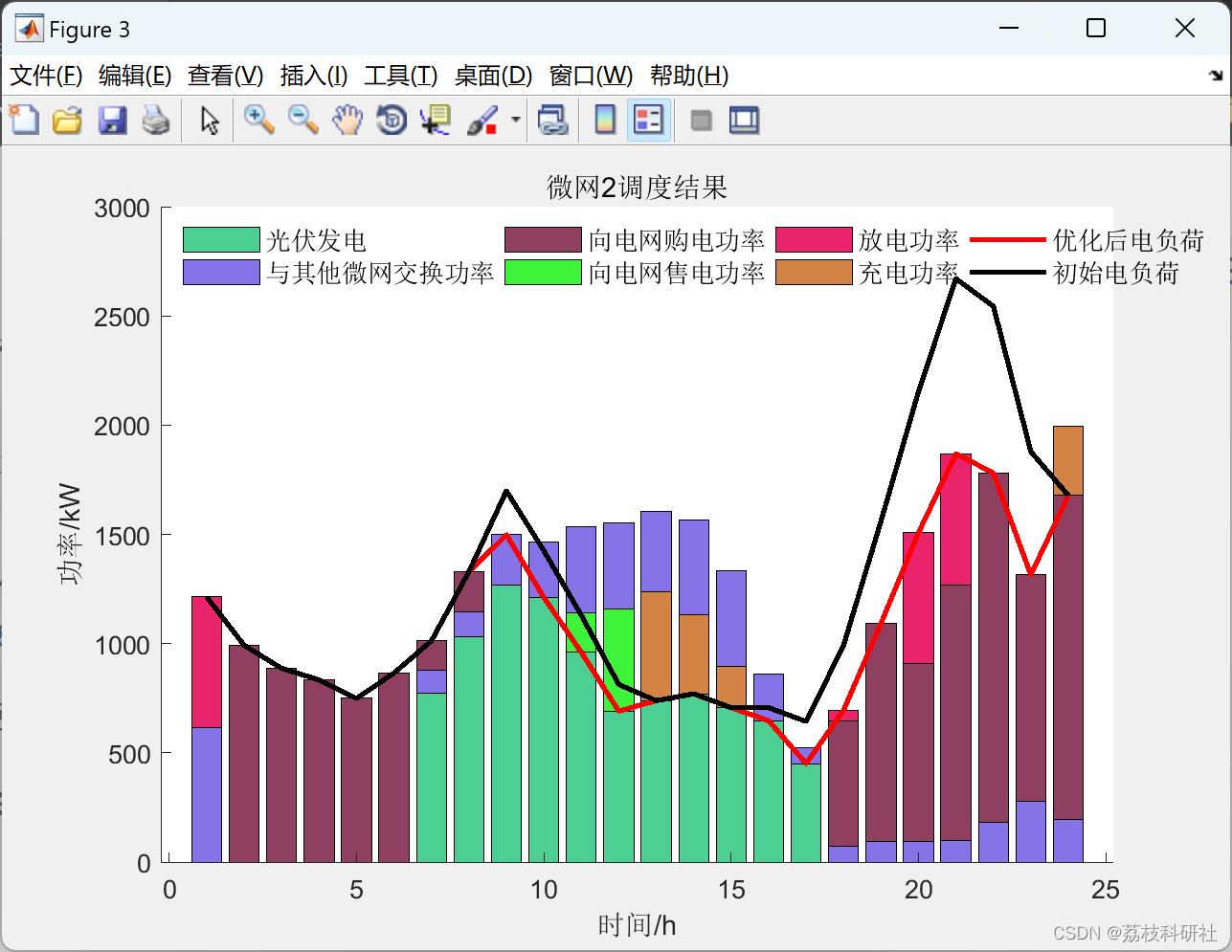
📚2 运行结果

 

 

 

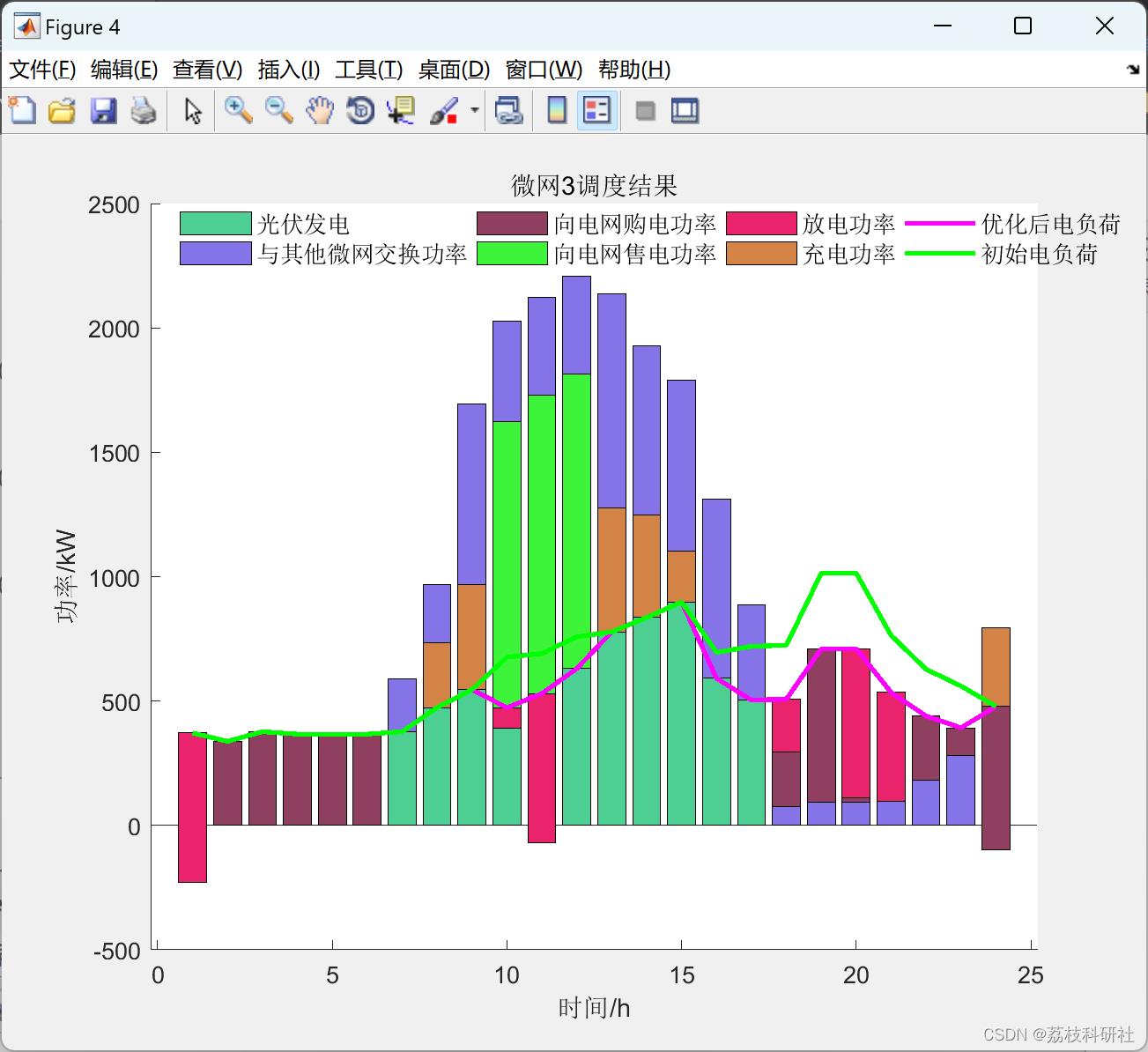
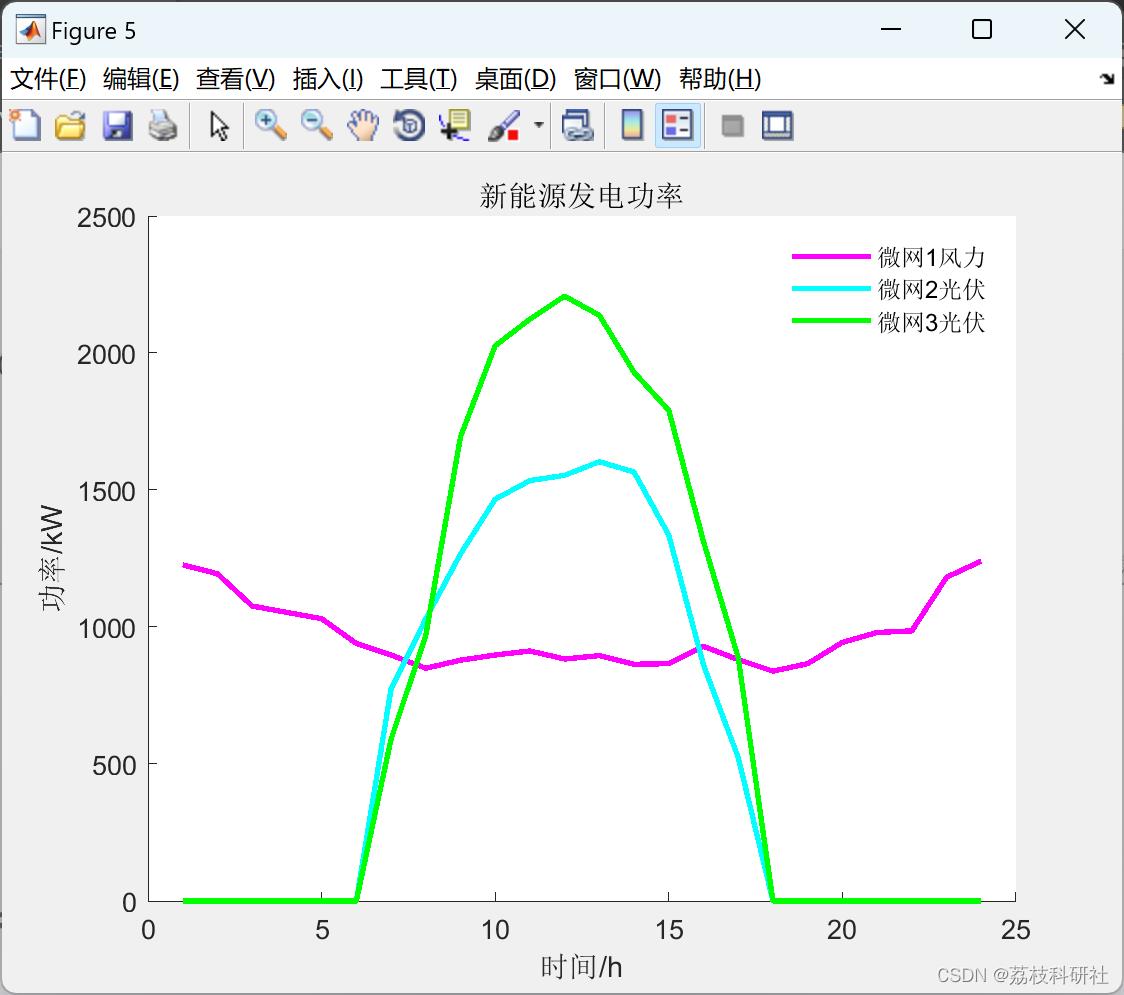
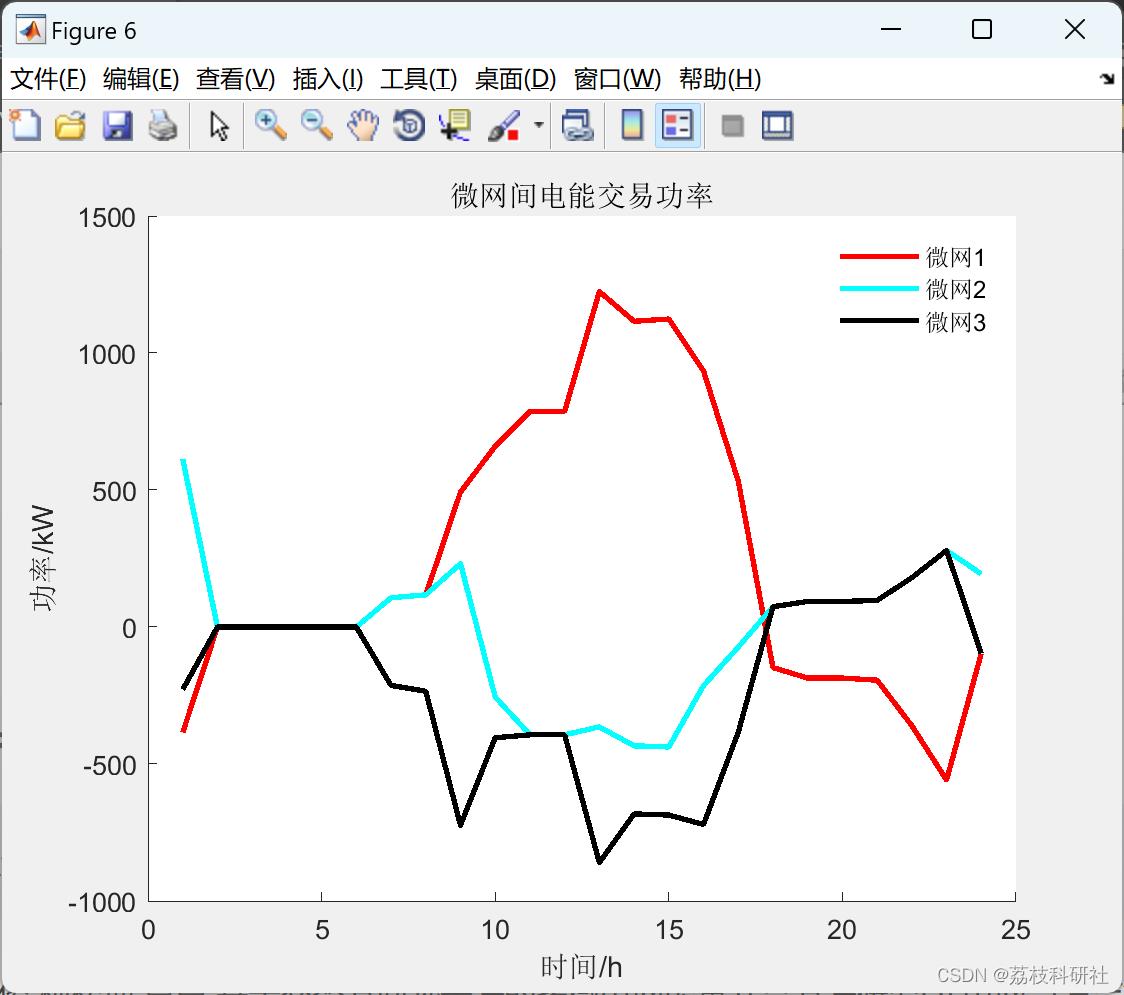
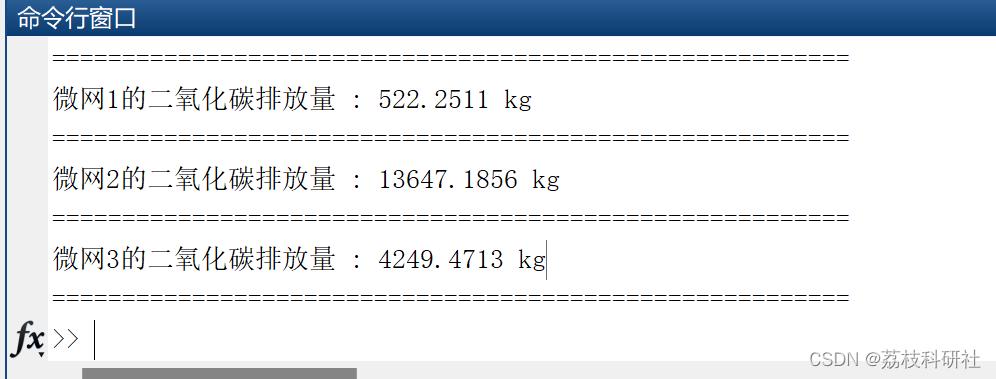
🎉3 参考文献

部分理论来源于网络，如有侵权请联系删除。

[1]高松,何俊,杨松坤,肖白.基于交替方向乘子法的多微电网能量共享方法研究[J].电网与清洁能源,2022,38(06):113-120.

[2]邝凯旋,张赟宁.基于ADMM算法的微电网多目标优化调度[J].电力科学与工程,2019,35(08):54-59.

🌈4 Matlab代码实现

[ML]交替方向乘子法(ADMM)简明梳理

交替方向乘子法(ADMM)简明梳理

本文对ADMM所涉及的一些数学知识进行简单的讲解, 并在最后汇总, 写出ADMM的基本形式.

本文对推导过程酌情省略.

拉格朗日乘子法

给定二元函数(z=f(x,y))和约束条件(psi(x,y)=0), 求二元函数(z=f(x,y))在约束条件下的极值点. 该问题可以用拉格朗日乘子法解:

首先做拉格朗日函数

[L(x,y,lambda)=f(x,y)+lambdapsi(x,y) ]

其中(lambda)为参数.

令上式对所有自变量的一阶偏导等于零, 即

[egin{cases} frac{partial L(x,y,lambda)}{partial x}=0\frac{partial L(x,y,lambda)}{partial y}=0\frac{partial L(x,y,lambda)}{partiallambda}=0 end{cases} ]

由上式解出(x), (y)及(lambda), 如此求得的((x,y)), 就是函数(z=f(x,y))在约束条件(psi(x,y)=0)下的可能极值点. 若这样的点只有一个, 由实际问题可直接确定此点即所求的点.

对偶上升法

首先需要简单介绍一下凸函数的定义. 凸函数比较直观的含义即为函数上任意两点的连线都在函数值之上, 二维上的典型是(y=x^2), 形如下凸的曲线, 三维上的典型是(z=x^2+y^2), 形如山谷.

接下来提出一个基础问题:

设函数(f(x))是一个凸函数, 约束条件为(Ax=b), 求函数(f(x))的最小值.

即

[ ext{min} f(x)\text{s.t.} Ax=b ]

写出该问题的拉格朗日函数

[L(x,y)=f(x)+y^T(Ax-b) ]

其中(y)是拉格朗日乘子, 也称为对偶变量.

对偶函数为

[g(x)=mathop{ ext{inf}}limits_xL(x,y)=-f^*(-A^Ty)-b^Ty ]

其中inf代表下确界, (f^*)代表(f)的共轭函数.

在满足一定条件的情况下, 对偶问题和原问题的最优值相等. 设原问题最优值为(x^*), 对偶问题最优值为(y^*), 则

[x^*=mathop{ ext{arg min}}limits_xL(x,y^*) ]

则可以通过对偶上升法, 通过梯度上升法迭代求解, 即

[x^{k+1}=mathop{ ext{arg min}}limits_xL(x,y^k)y^{k+1}=y^k+alpha_k(Ax^{k+1}-b) ]

增广拉格朗日乘子法

在原拉格朗日乘子法的基础上加入惩罚项, 即为增广拉格朗日乘子法, 形如

[L_ ho(x,y)=f(x)+y^T(Ax-b)+frac{ ho}{2}Vert Ax-bVert_2^2 ]

其中( ho>0), 称为惩罚参数.

在增广拉格朗日乘子法下, 原问题变为

[mathop{ ext{min}}limits_xf(x)+frac{ ho}{2}Vert Ax-bVert_2^2\text{s.t.} Ax=b ]

对偶上升迭代更新为

[x^{k+1}=mathop{ ext{arg min}}limits_xL_ ho(x,y^k)y^{k+1}=y^k+ ho(Ax^{k+1}-b) ]

交替方向乘子法

将原问题推广到多个参数的情形下

[mathop{ ext{min}}limits_xf(x)+g(z)\text{s.t.} Ax+Bz=c ]

其中(xinmathbb{R}^n,zinmathbb{R}^m,cinmathbb{R}^p,Ainmathbb{R}^{p imes n},Binmathbb{R}^{p imes m}).

其拉格朗日函数可以写为

[L_ ho(x,z,y)=f(x)+g(z)+y^T(Ax+bz-c)+frac{ ho}{2}Vert Ax+Bz-cVert_2^2 ]

其更新迭代形式为

[x^{k+1}=mathop{ ext{arg min}}limits_xL_ ho(x,z^k,y^k)z^{k+1}=mathop{ ext{arg min}}limits_zL_ ho(x^{k+1},z,y^k)y^{k+1}=y^k+ ho(Ax^{k+1}+Bz^{k+1}-c) ]

其中( ho>0).