剑指offer梯度消失和梯度爆炸

Posted 2023-04-05 .别拖至春天.

【剑指offer】系列文章目录

BN层详解
交叉熵损失函数

---

文章目录

• 【剑指offer】系列文章目录
• 梯度消失和梯度爆炸
• 为什么会产生梯度消失和梯度爆炸
• 代码示例

---

梯度消失和梯度爆炸

梯度消失和梯度爆炸是深度神经网络中常见的问题，这些问题可能导致模型无法训练或者训练过程非常缓慢。
【文末配有代码，可以参考代码案例进行理解以下概念】

• 梯度消失指的是在反向传播过程中，模型的某些层的梯度非常小，甚至接近于0，导致这些层的参数几乎无法更新。这种情况产生的原因有：一是在深层网络中，当网络层数较多时，梯度会在反向传播过程中多次相乘，使得梯度值逐渐变小，最终消失。当梯度消失时，网络的学习效果会变得非常差，甚至无法训练。二是采用了不合适的损失函数，比如sigmoid。当梯度消失发生时，接近于输出层的隐藏层由于其梯度相对正常，所以权值更新时也就相对正常，但是当越靠近输入层时，由于梯度消失现象，会导致靠近输入层的隐藏层权值更新缓慢或者更新停滞。这就导致在训练时，只等价于后面几层的浅层网络的学习。

• 梯度爆炸指的是在反向传播过程中，模型的某些层的梯度非常大，甚至超过了计算机可以表示的范围，导致这些层的参数发生了非常大的变化。这种情况通常发生在深度神经网络中，当网络层数较多时，梯度会在反向传播过程中多次相乘，使得梯度值逐渐变大，最终爆炸。当梯度爆炸时，网络的学习效果也会变得非常差，甚至无法训练。梯度爆炸会伴随一些细微的信号，如：①模型不稳定，导致更新过程中的损失出现显著变化；②训练过程中，在极端情况下，权重的值变得非常大，以至于溢出，导致模型损失变成 NaN等等。

---

为什么会产生梯度消失和梯度爆炸

梯度消失：
根据链式法则，如果每一层神经元对上一层的输出的偏导乘上权重结果都小于1的话，那么即使这个结果是0.99，在经过足够多层传播之后，误差对输入层的偏导会趋于0
关于梯度消失，以sigmoid函数为例子，sigmoid函数使得输出在[0,1]之间。

事实上x到了一定大小，经过sigmoid函数的输出范围就很小了，参考下图

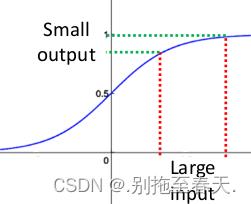
如果输入很大，其对应的斜率就很小，我们知道，其斜率（梯度）在反向传播中是权值学习速率。所以就会出现如下的问题：
在深度网络中，如果网络的激活输出很大，其梯度就很小，学习速率就很慢。假设每层学习梯度都小于最大值0.25，网络有n层，因为链式求导的原因，第一层的梯度小于0.25的n次方，所以学习速率就慢，对于最后一层只需对自身求导1次，梯度就大，学习速率就快。
这会造成的影响是在一个很大的深度网络中，浅层基本不学习，权值变化小，后面几层一直在学习，结果就是，后面几层基本可以表示整个网络，失去了深度的意义。

代码示例

代码如下（示例）：

import torch
import torch.nn as nn
import numpy as np

# 定义一个五层的全连接神经网络
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(1, 10)
        self.fc2 = nn.Linear(10, 10)
        self.fc3 = nn.Linear(10, 10)
        self.fc4 = nn.Linear(10, 10)
        self.fc5 = nn.Linear(10, 1)

    def forward(self, x):
        x = torch.relu(self.fc1(x))
        x = torch.relu(self.fc2(x))
        x = torch.relu(self.fc3(x))
        x = torch.relu(self.fc4(x))
        x = self.fc5(x)
        return x

# 定义一个计算权重梯度的函数
def compute_gradient(net, x):
    y = net(x)
    loss = torch.sum(y)
    loss.backward()
    gradients = [p.grad for p in net.parameters()]
    return gradients

# 定义一个计算梯度变化的函数
def compute_gradient_change(gradients1, gradients2):
    gradient_change = []
    for g1, g2 in zip(gradients1, gradients2):
        if g1 is None or g2 is None:
            gradient_change.append(None)
        else:
            gradient_change.append(torch.norm(g1 - g2) / torch.norm(g1))
    return gradient_change

# 定义一个计算梯度的函数
def compute_gradient_norm(gradients):
    gradient_norm = [torch.norm(g) for g in gradients if g is not None]
    return gradient_norm

# 定义一个训练函数
def train(net, optimizer, x, num_epochs=1000):
    for epoch in range(num_epochs):
        optimizer.zero_grad()
        y = net(x)
        loss = torch.sum(y)
        loss.backward()
        optimizer.step()

# 构造输入数据
x = torch.linspace(-1, 1, 100).reshape(-1, 1)

# 计算梯度变化
net1 = Net()
net2 = Net()
gradients1 = compute_gradient(net1, x)
optimizer1 = torch.optim.SGD(net1.parameters(), lr=0.1)
train(net1, optimizer1, x, num_epochs=100)
gradients2 = compute_gradient(net1, x)
# 计算梯度变化
gradient_change1 = compute_gradient_change(gradients1, gradients2)

# 计算梯度范数
gradient_norm1 = compute_gradient_norm(gradients2)

# 修改激活函数为sigmoid
class NetSigmoid(nn.Module):
    def __init__(self):
        super(NetSigmoid, self).__init__()
        self.fc1 = nn.Linear(1, 10)
        self.fc2 = nn.Linear(10, 10)
        self.fc3 = nn.Linear(10, 10)
        self.fc4 = nn.Linear(10, 10)
        self.fc5 = nn.Linear(10, 1)

    def forward(self, x):
        x = torch.sigmoid(self.fc1(x))
        x = torch.sigmoid(self.fc2(x))
        x = torch.sigmoid(self.fc3(x))
        x = torch.sigmoid(self.fc4(x))
        x = self.fc5(x)
        return x

# 计算梯度变化
net3 = NetSigmoid()
gradients1 = compute_gradient(net3, x)
optimizer3 = torch.optim.SGD(net3.parameters(), lr=0.1)
train(net3, optimizer3, x, num_epochs=100)
gradients2 = compute_gradient(net3, x)
gradient_change2 = compute_gradient_change(gradients1, gradients2)

# 计算梯度范数
gradient_norm2 = compute_gradient_norm(gradients2)

print('Gradient change (ReLU):', gradient_change1)
print('Gradient norm (ReLU):', gradient_norm1)
print('Gradient change (sigmoid):', gradient_change2)
print('Gradient norm (sigmoid):', gradient_norm2)

输出结果：

Gradient change (ReLU): [tensor(nan), tensor(nan), tensor(nan), tensor(nan), tensor(nan), tensor(nan), tensor(nan), tensor(nan), tensor(nan), tensor(0.)]
Gradient norm (ReLU): [tensor(nan), tensor(nan), tensor(nan), tensor(nan), tensor(nan), tensor(nan), tensor(nan), tensor(nan), tensor(nan), tensor(200.)]
Gradient change (sigmoid): [tensor(0.), tensor(0.), tensor(0.), tensor(0.), tensor(0.), tensor(0.), tensor(0.), tensor(0.), tensor(0.), tensor(0.)]
Gradient norm (sigmoid): [tensor(6.4147e-05), tensor(0.0017), tensor(0.0174), tensor(0.0106), tensor(0.0838), tensor(0.0480), tensor(0.1575), tensor(0.0573), tensor(632.4555), tensor(200.)]

前两行输出是梯度爆炸的效果，后两行是梯度消失的效果，具体含义可结合代码了解
使用sigmoid。当梯度消失发生时，接近于输出层的隐藏层由于其梯度相对正常，所以权值更新时也就相对正常，但是当越靠近输入层时，由于梯度消失现象，会导致靠近输入层的隐藏层权值更新缓慢或者更新停滞。这就导致在训练时，只等价于后面几层的浅层网络的学习。

---

TensorFlow2 手把手教你避开梯度消失和梯度爆炸

TensorFlow2 手把手教你避开梯度消失和梯度爆炸

• 梯度消失 & 梯度爆炸
• • 梯度消失
  • 梯度爆炸
• 张量限幅
• • tf.clip_by_value
  • tf.clip_by_norm
• mnist 展示梯度爆炸
• • 完整代码
  • 输出结果

梯度消失 & 梯度爆炸

输出结果:

vanish: 0.025517964452291125
explode: 37.78343433288728

梯度消失

梯度消失问题 (Vanishing gradient problem). 如果导数小于 1, 随着网络层数的增加梯度跟新会朝着指数衰减的方向前进, 这就是梯度消失.

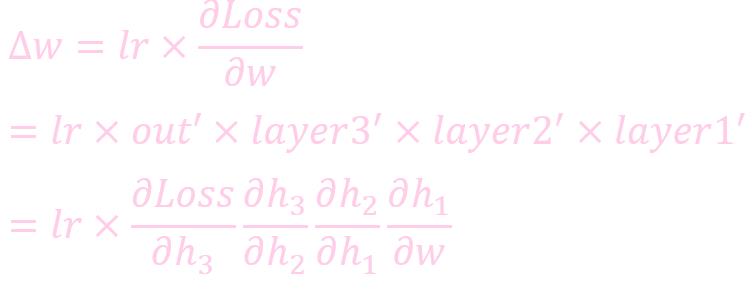
当导数小于 1 的时候, 层数越多, 梯度就越小, 即梯度消失.

梯度爆炸

梯度爆炸问题 (Exploding gradient problem). 如果导数大于 1, 随着网络层数的增加梯度跟新会朝着指数增加的方向前进, 这就是梯度爆炸.

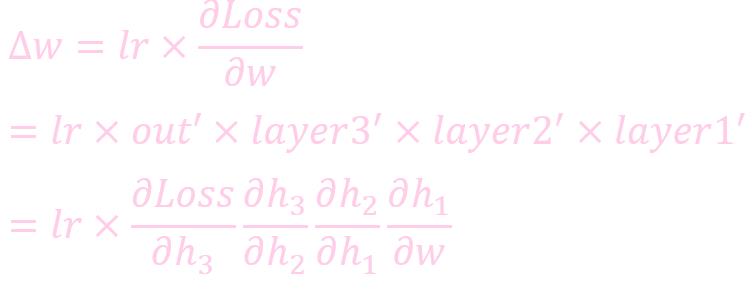
当导数大于 1 的时候, 层数越多, 梯度就越大, 即梯度爆炸.

张量限幅

通过张量限幅, 我们可以有效解决梯度爆炸问题.

tf.clip_by_value

我们可以通过tf.clip_by_value函数来实现张量限幅.

格式:

tf.clip_by_value(
    t, clip_value_min, clip_value_max, name=None
)

参数:

• t: 传入的张量
• clip_value_min: 下限
• clip_value_max: 上限
• name: 数据名称

例子:

# clip_by_value
a = tf.range(10)
print(a)

b = tf.maximum(a, 2)
print(b)

c = tf.minimum(a, 8)
print(c)

d = tf.clip_by_value(a, 2, 8)
print(d)

输出结果:

tf.Tensor([0 1 2 3 4 5 6 7 8 9], shape=(10,), dtype=int32)
tf.Tensor([2 2 2 3 4 5 6 7 8 9], shape=(10,), dtype=int32)
tf.Tensor([0 1 2 3 4 5 6 7 8 8], shape=(10,), dtype=int32)
tf.Tensor([2 2 2 3 4 5 6 7 8 8], shape=(10,), dtype=int32)

tf.clip_by_norm

tf.clip_by_norm可以对梯度进行裁剪, 防止梯度爆炸.

格式:

tf.clip_by_norm(
    t, clip_norm, axes=None, name=None
)

参数:

• t: 传入的张量
• clip_norm: 定义最大限幅
• axes: 计算尺寸
• name: 数据名称

例子:

# clip_by_normal
a = tf.random.normal([2, 2], mean=10)
print(a)
print(tf.norm(a))  # 范数

b = tf.clip_by_norm(a, 15)
print(b)
print(tf.norm(b))  # 范数

输出结果:

tf.Tensor(
[[ 9.33037  10.703022]
 [ 9.788097  9.713704]], shape=(2, 2), dtype=float32)
tf.Tensor(19.793266, shape=(), dtype=float32)
tf.Tensor(
[[7.070867  8.111109 ]
 [7.417748  7.3613706]], shape=(2, 2), dtype=float32)
tf.Tensor(15.0, shape=(), dtype=float32)

mnist 展示梯度爆炸

为了实现梯度爆炸, 我们把学习率设为 0.1.

完整代码

# 读取训练集的特征值和目标值
(x, y), _ = tf.keras.datasets.mnist.load_data()

# 转换为0~1的形式
x = tf.convert_to_tensor(x, dtype=tf.float32) / 255

# 转换成one_hot编码
y = tf.one_hot(y, depth=10)

# 批次分割
train_db = tf.data.Dataset.from_tensor_slices((x, y)).batch(256).repeat(30)


def main():
    # 生成w1形状为[784, 512]的截断正态分布, 中心为0, 标差为0.1
    w1 = tf.Variable(tf.random.truncated_normal([784, 512], stddev=0.1))

    # 生成b1形状为[512]初始化为0
    b1 = tf.Variable(tf.zeros([512]))

    # 生成w2形状为[512, 256]的截断正态分布, 中心为0, 标差为0.1
    w2 = tf.Variable(tf.random.truncated_normal([512, 256], stddev=0.1))

    # 生成b2形状为[256]初始化为0
    b2 = tf.Variable(tf.zeros([256]))

    # 生成w3形状为[256, 10]的截断正态分布, 中心为0, 标差为0.1
    w3 = tf.Variable(tf.random.truncated_normal([256, 10], stddev=0.1))

    # 生成b3形状为[10]初始化为0
    b3 = tf.Variable(tf.zeros([10]))

    # 优化器
    optimizer = tf.keras.optimizers.SGD(learning_rate=0.1)  # 梯度下降

    for step, (x, y) in enumerate(train_db):

        # 把x平铺 [256, 28, 28] => [256, 784]
        x = tf.reshape(x, [-1, 784])

        with tf.GradientTape() as tape:

            # 第一个隐层
            h1 = x @ w1 + b1
            h1 = tf.nn.relu(h1)  # 激活

            # 第二个隐层
            h2 = h1 @ w2 + b2
            h2 = tf.nn.relu(h2)  # 激活

            # 输出层
            out = h2 @ w3 + b3

            # 计算损失函数
            loss = tf.square(y - out)
            loss = tf.reduce_mean(loss)

            # 计算梯度
            grads = tape.gradient(loss, [w1, b1, w2, b2, w3, b3])

            # 调试输出剪切前的范数
            print("================before===============")
            for g in grads:
                print(tf.norm(g))

            grads, _ = tf.clip_by_global_norm(grads, 15)

            # 调试输出剪切后的范数
            print("================after===============")
            for g in grads:
                print(tf.norm(g))

            optimizer.apply_gradients(zip(grads, [w1, b1, w2, b2, w3, b3]))  # 跟新权重


if __name__ == '__main__':
    main()

输出结果

================before===============
tf.Tensor(5.5961547, shape=(), dtype=float32)
tf.Tensor(0.87258744, shape=(), dtype=float32)
tf.Tensor(7.397964, shape=(), dtype=float32)
tf.Tensor(0.69156337, shape=(), dtype=float32)
tf.Tensor(9.840232, shape=(), dtype=float32)
tf.Tensor(0.8157242, shape=(), dtype=float32)
================after===============
tf.Tensor(5.5961547, shape=(), dtype=float32)
tf.Tensor(0.87258744, shape=(), dtype=float32)
tf.Tensor(7.397964, shape=(), dtype=float32)
tf.Tensor(0.69156337, shape=(), dtype=float32)
tf.Tensor(9.840232, shape=(), dtype=float32)
tf.Tensor(0.8157242, shape=(), dtype=float32)
================before===============
tf.Tensor(18.01539, shape=(), dtype=float32)
tf.Tensor(2.9375393, shape=(), dtype=float32)
tf.Tensor(21.330334, shape=(), dtype=float32)
tf.Tensor(2.1504176, shape=(), dtype=float32)
tf.Tensor(21.820374, shape=(), dtype=float32)
tf.Tensor(2.0918982, shape=(), dtype=float32)
================after===============
tf.Tensor(7.5730414, shape=(), dtype=float32)
tf.Tensor(1.2348388, shape=(), dtype=float32)
tf.Tensor(8.966527, shape=(), dtype=float32)
tf.Tensor(0.90396047, shape=(), dtype=float32)
tf.Tensor(9.172523, shape=(), dtype=float32)
tf.Tensor(0.8793609, shape=(), dtype=float32)
================before===============
tf.Tensor(0.5821787, shape=(), dtype=float32)
tf.Tensor(0.0859229, shape=(), dtype=float32)
tf.Tensor(0.7110027, shape=(), dtype=float32)
tf.Tensor(0.082481824, shape=(), dtype=float32)
tf.Tensor(0.51846975, shape=(), dtype=float32)
tf.Tensor(0.1655324, shape=(), dtype=float32)
================after===============
tf.Tensor(0.5821787, shape=(), dtype=float32)
tf.Tensor(0.0859229, shape=(), dtype=float32)
tf.Tensor(0.7110027, shape=(), dtype=float32)
tf.Tensor(0.082481824, shape=(), dtype=float32)
tf.Tensor(0.51846975, shape=(), dtype=float32)
tf.Tensor(0.1655324, shape=(), dtype=float32)

... ...