学习笔记计算机视觉与深度学习(3.卷积与图像去噪/边缘提取/纹理表示)

Posted 2023-04-03 xhyu61

学习视频：
鲁鹏-计算机视觉与深度学习

同系列往期笔记：
【学习笔记】计算机视觉与深度学习(1.线性分类器)
【学习笔记】计算机视觉与深度学习(2.全连接神经网络)

1 卷积

噪声点：该点的像素和周围像素点的差异很大，如图中左图的253。
通过以该点为中心的9个点的像素值取均值来替代该点原本的像素值。

加权的权值$\frac{1}{9}$，我们通常存储在一个上面这样的模板当中，我们称这个模板为卷积核，也称滤波核。

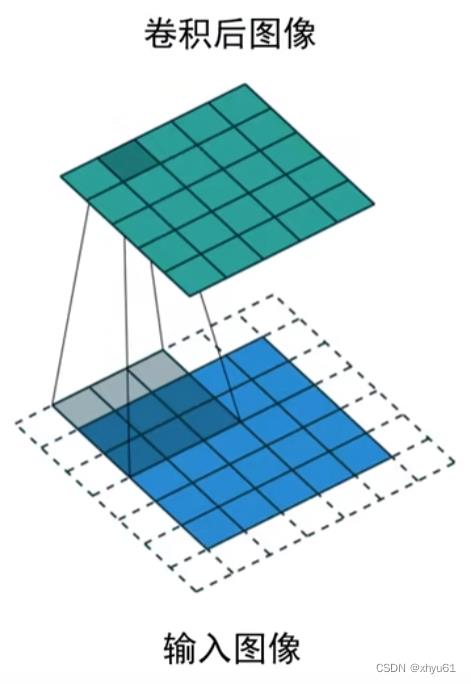
下面的蓝色是输入的图像，上面的绿色是卷积后得到的输出图像。每一个像素点都有一个卷积核，通过卷积核得到输出的像素值。

令$F$为图像，$H$为卷积核，$F$与$H$的卷积即为$R=F\ast H$。
$$R_{ij}=\sum _{u,v}{H}_{i-u,j-v}{F}_{u,v}$$

进行卷积操作前，我们要先对卷积核进行180°翻转。不过通常我们使用卷积时，卷积核都是对称的，所以后续不会强调翻转操作。

公式略抽象，举例说明。令：
$$F=\left[\begin{array}{ccc}{a}_{0,0}& a_{0,1}& a_{0,2}\\ a_{1,0}& a_{1,1}& a_{1,2}\\ a_{2,0}& a_{2,1}& a_{2,2}\end{array}\right]H=\left[\begin{array}{ccc}{b}_{-1,-1}& b_{-1,0}& b_{-1,1}\\ b_{0,-1}& b_{0,0}& b_{0,1}\\ b_{1,-1}& b_{1,0}& b_{1,1}\end{array}\right]$$
卷积后可以得到：

$$\begin{array}{rl}{R}_{ij}& =a_{0,0}{b}_{1,1}+a_{0,1}{b}_{1,0}+a_{0,2}{b}_{1,-1}\\ & +a_{1,0}{b}_{0,1}+a_{1,1}{b}_{0,0}+a_{1,2}{b}_{0,-1}\\ & +a_{2,0}{b}_{-1,1}+a_{2,1}{b}_{-1,0}+a_{2,2}{b}_{-1,-1}\end{array}$$

综上，通过这个公式，我们就可以使用$H$将$F$卷积到$R$域上去。

卷积示例

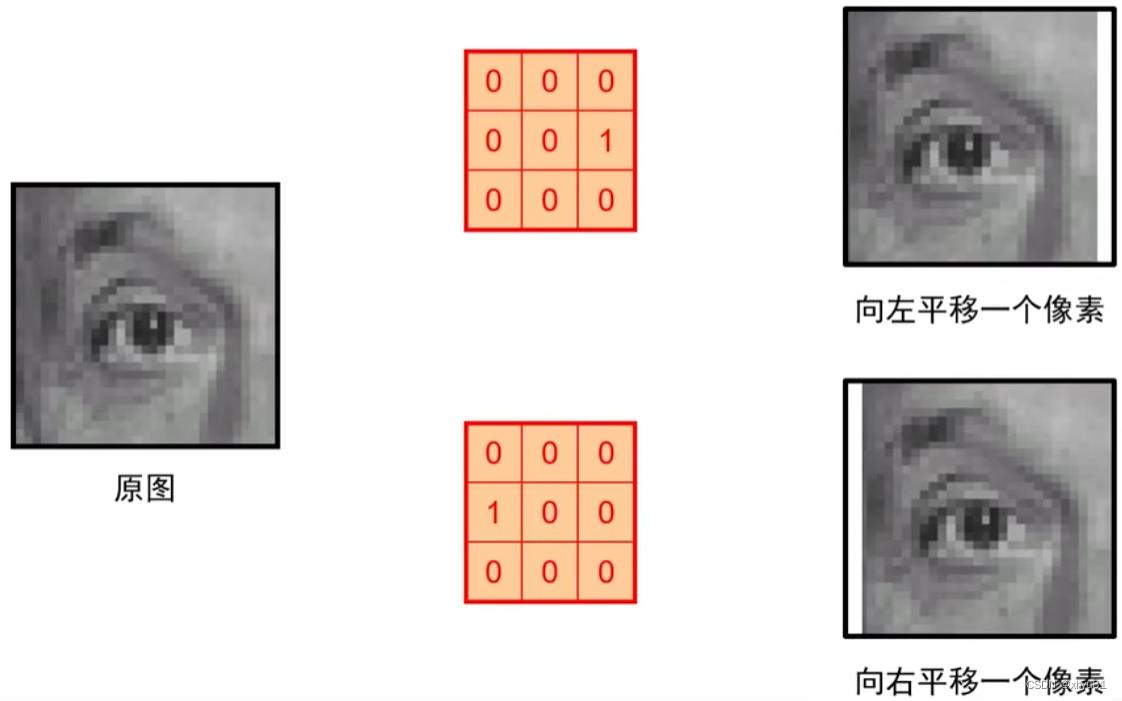
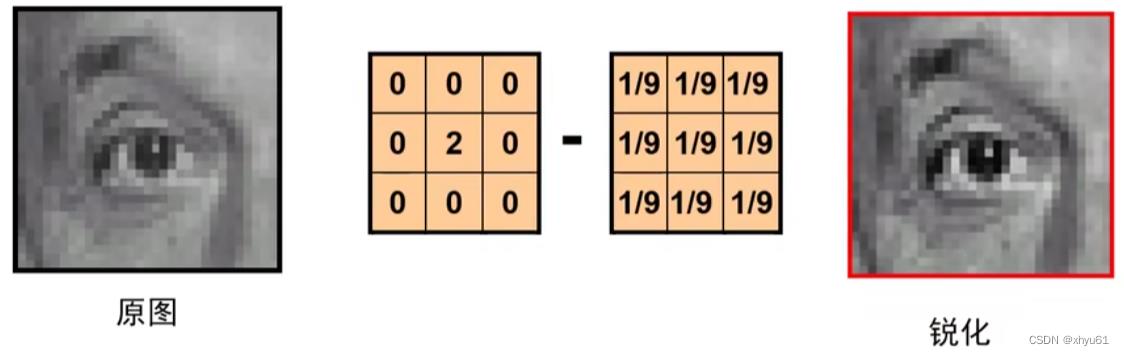
锐化原理见下图

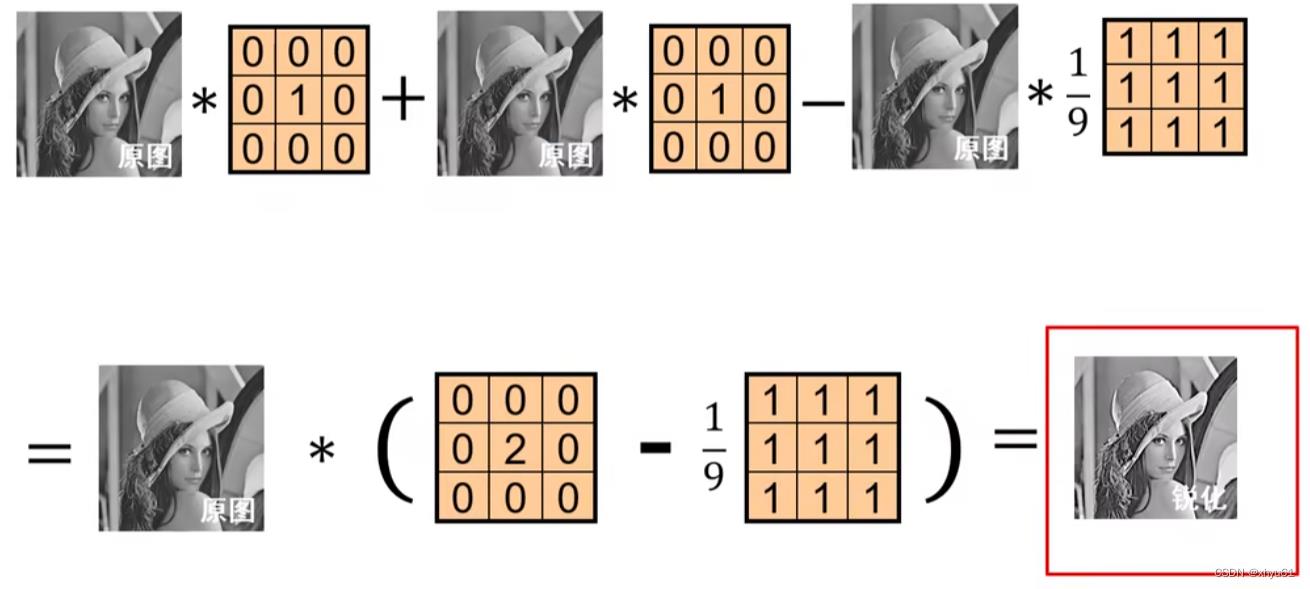
更好地理解卷积所起到的滤波器的效果，可以参考这个网站：
Image-Kernels

卷积的性质

令$f_i$为卷积前的图像，$filter(f_i)$为卷积后的图像， s h i f t ( f i ) shift(f_i) shift(f

计算机视觉与深度学习 笔记EP1

主要资料来源：（P1-P3）计算机视觉与深度学习 北京邮电大学 鲁鹏 清晰版合集（完整版）_哔哩哔哩_bilibili

数据驱动的图像分类方法  

        数据集收集

• 数据集划分与预处理

        训练集：确定超参数时对分类器参数进行学习

        验证集：用于选择超参数

        测试集：评估泛化能力

        k折交叉验证：

           数据预处理1（去均值和归一化）：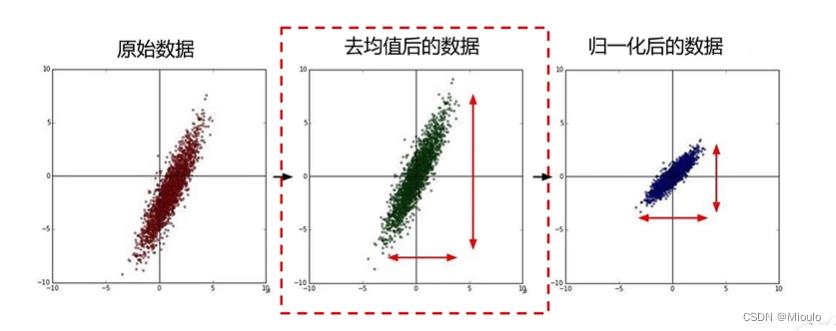        

去均值：度量与平均值之间的差距

归一化：将数据映射在一个区间内，是数值范围几乎相等

参考和其他数据预处理方法：数据预处理的几个名词：中心化，归一化，去相关，白化_m0_37708267的博客-CSDN博客_去相关处理

---

 

 

 

        分类器的设计与学习

 

---

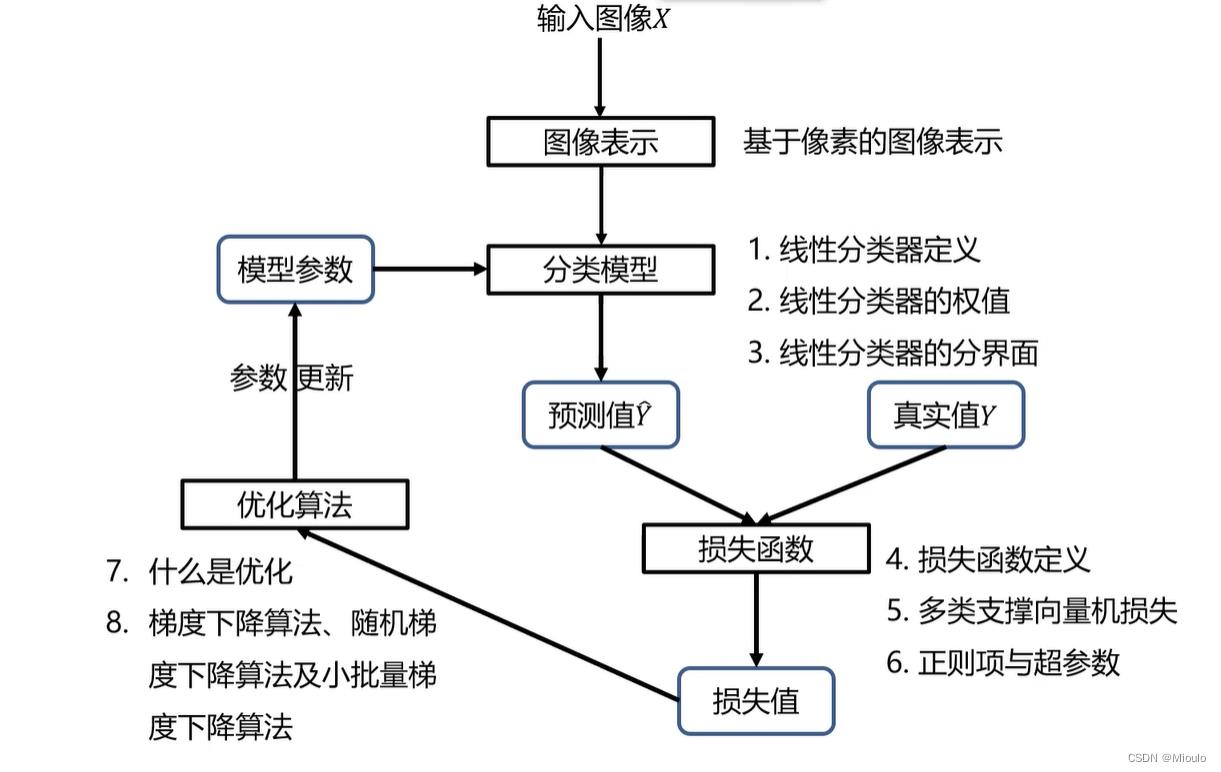
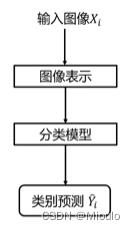
图像表示

• 像素表示：RGB三通道表示、灰度图像单通道表示、二值化图像
• 全局特征表示（GIST）：在全图中抽取特征，如颜色特征、纹理特征、形状特征。如强度直方图。
• 局部特征表示：分割区块然后分析各区块的特征（优点是不会因遮挡受影响）

        参考：(4条消息) 图像处理局部和全局特征 - CSDN

---

分类模型

• 线性分类器

        

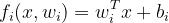
        x是输入的图像向量，i取不同的值代表第i个类别

        w即是这类线性分类器的权值向量，b为这类线性分类器的偏置

        w与b通过训练更新和优化

        决策时，取f权值最大的类，就决策该图像向量属于这个类

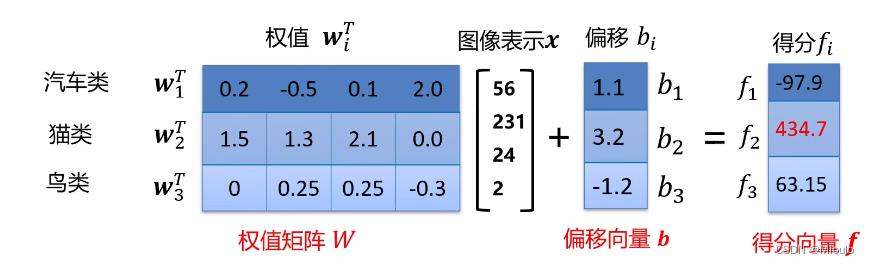
         矩阵表示后，f、W、b变为一个矩阵，行数维度取决于其类别个数

        

        示例：一个训练完成的权值向量矩阵，包含了10个类 

• 神经网络分类器     

（待整理）

---

损失函数

        损失函数时一个函数，度量分裂器预测值与真实值的差异程度，通常规定输出为一个非负实数

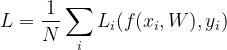
        L为数据集损失，是数据集中所有样本损失的平均值

        接下来，确定恰当合适的L函数是训练出一个好的分类器的关键

•         多类支撑向量机损失（损失函数的一种）

预测分数的定义如下：

第i个样本的多类支撑向量损失函数的定义如下：

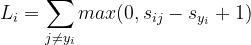
函数解读：即正确类别的得分比这个样本的其他的不正确类别高出1分，记为损失为0，否则产生损失并计算出值L

•         正则项损失

        

        使用原因：对于矩阵W，可能会出现两个列向量w使损失函数为0，此时无法作出决策，因此添加一个正则项损失λR（W）来解决这个问题。该值只与权值向量有关

        λ作为一个超参数（指机器学习过程之前就设置的参数，不是通过训练得到的参数数据，与W区分开来），控制正则损失在总损失中的占比

        L2正则项：

        k,l表示第k行第l列

        函数解读：发现这个正则损失函数描述的是权值向量的分散程度，越分散，这个损失越小（越分散，我们可以理解成考虑了更多维度的特征，集中的话可能只是用了某个维度的特征，从而使决策有偶然性）以此来解决数据损失相等的情况       

---

优化算法

        参数优化：利用损失函数的输出值作为反馈信号来调整分类器的参数，提高分类器预测性能

        L是一个关于参数W的函数，我们要找到使损失函数L达到最优的那组参数W使  

• 梯度下降

 

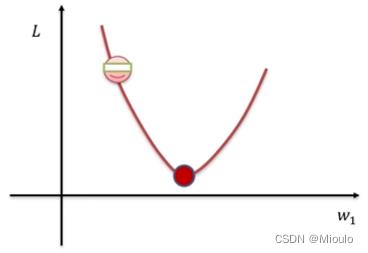
        沿着负梯度方向行进（步长），会是损失函数最快达到极值（极小值），从而使这个分类器达到最好的状态，这种思路即是梯度下降优化算法

       损失函数的梯度：

        

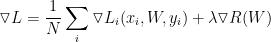
注意：计算出来的是一个矩阵向量

        设定一个超参数学习率μ，以此定义步长然后更新权值

        即：新权值=旧权值-学习率*权值的梯度

• 随机梯度下降

        每次随机选择一个样本然后更新梯度（比如200个样本，并不是用200个样本更新一次梯度/参数，而是每次用1个样本更新200次梯度/参数）

• 小批量随机梯度下降

        设定一个超参数m（代表每次选取m个样本）再进行训练更新参数

        m通常取32、64、128等2的倍数

        参考：(4条消息) 数值优化：一阶和二阶优化算法(Pytorch实现)_「已注销」的博客-CSDN博客

---

        分类器决策