DFS+记忆化剪枝--[NOIP2017 普及组] 棋盘
Posted Silver_bullet2004
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了DFS+记忆化剪枝--[NOIP2017 普及组] 棋盘相关的知识,希望对你有一定的参考价值。
[NOIP2017 普及组] 棋盘
题目背景
NOIP2017 普及组 T3
题目描述
有一个 m × m m \\times m m×m的棋盘,棋盘上每一个格子可能是红色、黄色或没有任何颜色的。你现在要从棋盘的最左上角走到棋盘的最右下角。
任何一个时刻,你所站在的位置必须是有颜色的(不能是无色的), 你只能向上、 下、左、 右四个方向前进。当你从一个格子走向另一个格子时,如果两个格子的颜色相同,那你不需要花费金币;如果不同,则你需要花费 $1 $个金币。
另外, 你可以花费 2 2 2 个金币施展魔法让下一个无色格子暂时变为你指定的颜色。但这个魔法不能连续使用, 而且这个魔法的持续时间很短,也就是说,如果你使用了这个魔法,走到了这个暂时有颜色的格子上,你就不能继续使用魔法; 只有当你离开这个位置,走到一个本来就有颜色的格子上的时候,你才能继续使用这个魔法,而当你离开了这个位置(施展魔法使得变为有颜色的格子)时,这个格子恢复为无色。
现在你要从棋盘的最左上角,走到棋盘的最右下角,求花费的最少金币是多少?
输入格式
第一行包含两个正整数$ m, n$,以一个空格分开,分别代表棋盘的大小,棋盘上有颜色的格子的数量。
接下来的$ n 行,每行三个正整数 行,每行三个正整数 行,每行三个正整数 x, y, c ,分别表示坐标为 , 分别表示坐标为 ,分别表示坐标为(x,y) 的格子有颜色 的格子有颜色 的格子有颜色 c$。
其中$ c=1$ 代表黄色,$ c=0$ 代表红色。 相邻两个数之间用一个空格隔开。 棋盘左上角的坐标为 ( 1 , 1 ) (1, 1) (1,1),右下角的坐标为 ( m , m ) ( m, m) (m,m)。
棋盘上其余的格子都是无色。保证棋盘的左上角,也就是 ( 1 , 1 ) (1, 1) (1,1) 一定是有颜色的。
输出格式
一个整数,表示花费的金币的最小值,如果无法到达,输出 − 1 -1 −1。
样例 #1
样例输入 #1
5 7
1 1 0
1 2 0
2 2 1
3 3 1
3 4 0
4 4 1
5 5 0
样例输出 #1
8
样例 #2
样例输入 #2
5 5
1 1 0
1 2 0
2 2 1
3 3 1
5 5 0
样例输出 #2
-1
提示
输入输出样例 1 说明
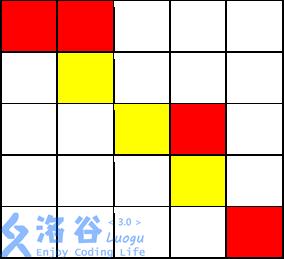
从 ( 1 , 1 ) (1,1) (1,1)开始,走到 ( 1 , 2 ) (1,2) (1,2)不花费金币
从 ( 1 , 2 ) (1,2) (1,2)向下走到 ( 2 , 2 ) (2,2) (2,2)花费 1 1 1 枚金币
从 ( 2 , 2 ) (2,2) (2,2)施展魔法,将 ( 2 , 3 ) (2,3) (2,3)变为黄色,花费 2 2 2 枚金币
从 ( 2 , 2 ) (2,2) (2,2)走到 ( 2 , 3 ) (2,3) (2,3)不花费金币
从 ( 2 , 3 ) (2,3) (2,3)走到 ( 3 , 3 ) (3,3) (3,3)不花费金币
从 ( 3 , 3 ) (3,3) (3,3)走到 ( 3 , 4 ) (3,4) (3,4)花费 1 1 1 枚金币
从 ( 3 , 4 ) (3,4) (3,4)走到 ( 4 , 4 ) (4,4) (4,4)花费 1 1 1 枚金币
从 ( 4 , 4 ) (4,4) (4,4)施展魔法,将 ( 4 , 5 ) (4,5) (4,5)变为黄色,花费$ 2$ 枚金币,
从 ( 4 , 4 ) (4,4) (4,4)走到 ( 4 , 5 ) (4,5) (4,5)不花费金币
从 ( 4 , 5 ) (4,5) (4,5)走到 ( 5 , 5 ) (5,5) (5,5)花费 1 1 1 枚金币
共花费 $8 $枚金币。
输入输出样例 2 说明
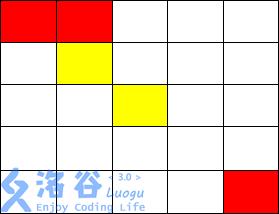
从 ( 1 , 1 ) ( 1, 1) (1,1)走到 ( 1 , 2 ) ( 1, 2) (1,2),不花费金币
从 ( 1 , 2 ) ( 1, 2) (1,2)走到 ( 2 , 2 ) ( 2, 2) (2,2),花费$ 1 $金币
施展魔法将 ( 2 , 3 ) ( 2, 3) (2,3)变为黄色,并从 ( 2 , 2 ) ( 2, 2) (2,2)走到 ( 2 , 3 ) ( 2, 3) (2,3)花费$ 2$ 金币
从 ( 2 , 3 ) ( 2, 3) (2,3)走到 ( 3 , 3 ) ( 3, 3) (3,3)不花费金币
从 ( 3 , 3 ) ( 3, 3) (3,3)只能施展魔法到达 ( 3 , 2 ) , ( 2 , 3 ) , ( 3 , 4 ) , ( 4 , 3 ) ( 3, 2),( 2, 3),( 3, 4),( 4, 3) (3,2),(2,3),(3,4),(4,3)
而从以上四点均无法到达 ( 5 , 5 ) ( 5, 5) (5,5),故无法到达终点,输出 − 1 -1 −1
数据规模与约定
对于 30 % 30\\% 30%的数据, 1 ≤ m ≤ 5 , 1 ≤ n ≤ 10 1 ≤ m ≤ 5, 1 ≤ n ≤ 10 1≤m≤5,1≤n≤10。
对于 60 % 60\\% 60%的数据, 1 ≤ m ≤ 20 , 1 ≤ n ≤ 200 1 ≤ m ≤ 20, 1 ≤ n ≤ 200 1≤m≤20,1≤n≤200。
对于 100 % 100\\% 100%的数据, 1 ≤ m ≤ 100 , 1 ≤ n ≤ 1 , 000 1 ≤ m ≤ 100, 1 ≤ n ≤ 1,000 1≤m≤100,1≤n≤1,000。
本来是想用DFS打暴力,没想到剪枝后跑的还是很快的全是0ms 呐
爆搜会超时,所以加上记忆化剪枝优化
1.用cost数组记录到达p, q时的最小花费,每次搜索前判断花费是否小于cost,否则不搜
2.用 j 布尔类型数组记录p, q 是否走过,走过的不搜
3.变色时变为与上一个位置相同的颜色则花费最小
4.颜色存储时有颜色的用1和2,无色存为0比较好判断
#include <bits/stdc++.h>
using namespace std;
/*
凭经验来说直接暴搜肯定会T
于是利用cost数组来保存最小花费
等同于剪枝的效果
每次在走到下一个点之前
先判断一下是否比之前更省钱
否则就不去搜了
由于不能连续使用两次魔法
所以dfs多传一个参数
用来记录魔法使用次数
*/
const int M = 105, N = 1005;
int m, n;
bool j[M][M];
int col[M][M];
int cost[M][M];
int a[4] = 1, -1, 0, 0, b[4] = 0, 0, 1, -1;
bool flag;
void dfs(int x, int y, int t)
if(x == m && y == m) flag = 1; return;
for(int i = 0; i < 4; i ++)
int p = x + a[i], q = y + b[i];
if(p <= 0 || p > m || q <= 0 || q > m) continue;
if(j[p][q]) continue;
if(!col[p][q])
//目标位置无色
if(t == 1) continue;
if(cost[p][q] > 2 + cost[x][y])
cost[p][q] = 2 + cost[x][y];
j[p][q] = 1;
col[p][q] = col[x][y];
dfs(p, q, 1);
j[p][q] = 0;
col[p][q] = 0;
else
if(col[x][y] == col[p][q])
//颜色相同
if(cost[p][q] > cost[x][y])
cost[p][q] = cost[x][y];
j[p][q] = 1;
dfs(p, q, 0);
j[p][q] = 0;
else
//颜色不同
if(cost[p][q] > 1 + cost[x][y])
cost[p][q] = 1 + cost[x][y];
j[p][q] = 1;
dfs(p, q, 0);
j[p][q] = 0;
int main()
cin >> m >> n;
for(int i = 1; i <= n; i ++)
int x, y, c;
cin >> x >> y >> c;
col[x][y] = c + 1;
//1红、2黄、0无色
memset(cost, 0x3f, sizeof cost);
j[1][1] = 1;
cost[1][1] = 0;
dfs(1, 1, 0);
if(flag) cout << cost[m][m];
else cout << -1;
return 0;
洛谷-----P1028 [NOIP2001 普及组] 数的计算

数的计算题解集合
DFS
把问题转化为对一颗多叉树的遍历,叶子的总数加上一个根节点的总数就是我们需要的结果
代码:
#include<iostream>
using namespace std;
class Solution {
public:
int SumNum(int num)
{
int sum =0;
//递归结束条件:
if (num<= 1)
return 1;
for (int i = 0; i <=num / 2; i++)
{
sum += SumNum(i);
}
return sum;
}
};
int main()
{
Solution s;
int n = 0;
cin >> n;
cout << s.SumNum(n) << endl;;
return 0;
}
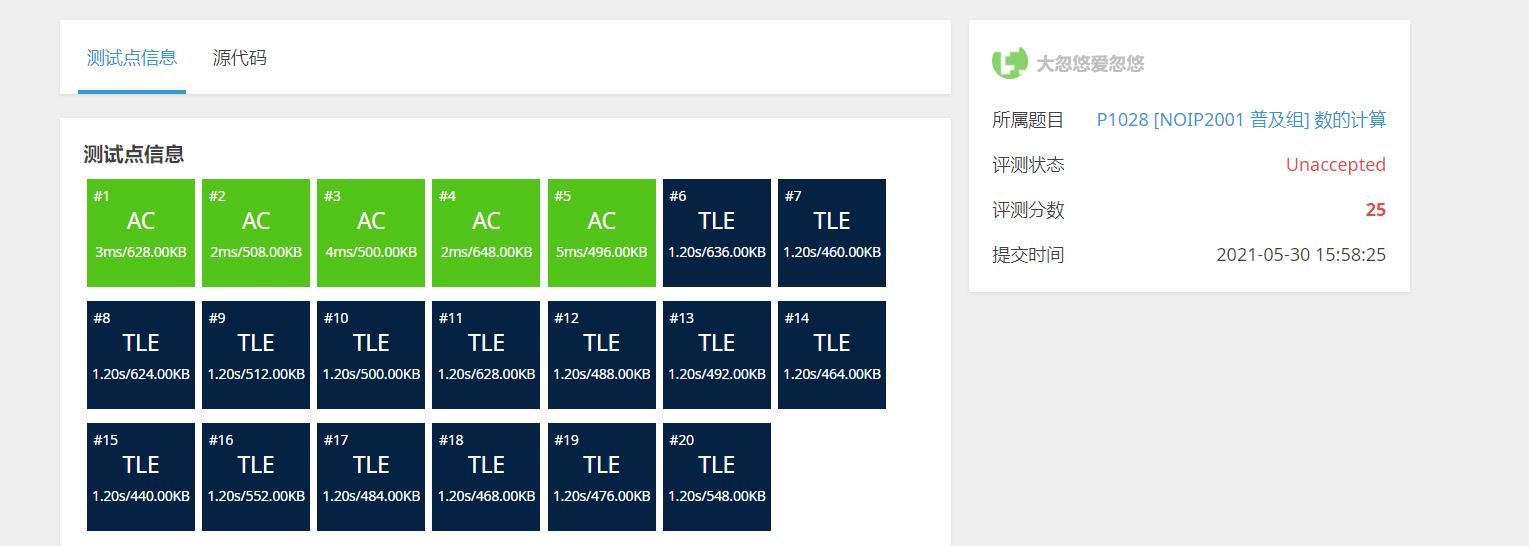
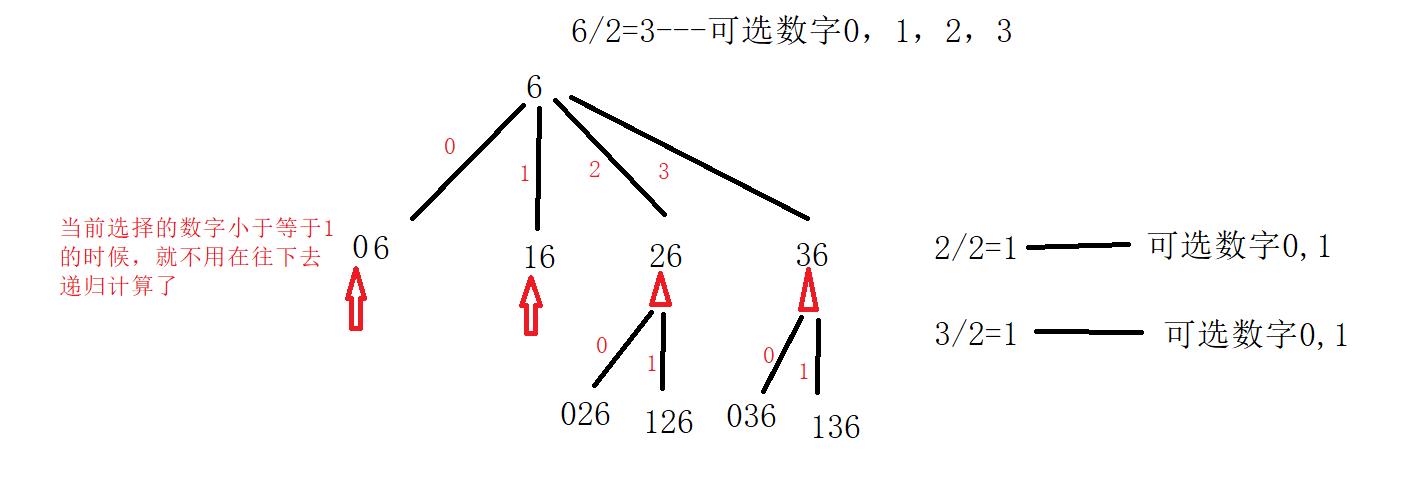
显然这里TLE,递归超时了
记忆化递归
首先思考,这里的重复计算出现在什么地方,这里我们才能对症下药,看下图:
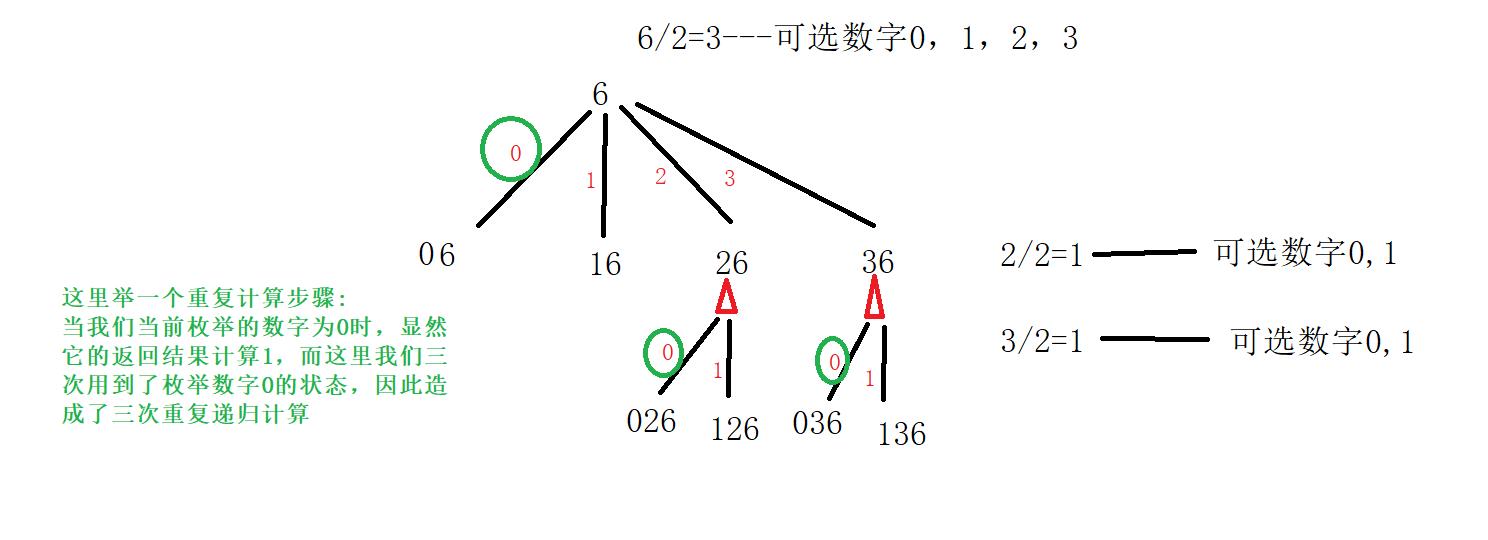
这里我们可以使用哈希表保存选择了当前数字后,得到的总数,等到下次用到的时候,直接返回即可
代码:
#include<iostream>
using namespace std;
#include<unordered_map>
class Solution {
unordered_map<int, int> cache;
public:
int SumNum(int num)
{
if (cache.find(num) != cache.end()) return cache[num];
int sum =0;
//递归结束条件:
if (num<= 1)
return 1;
for (int i = 0; i <=num / 2; i++)
{
sum += SumNum(i);
}
return cache[num]=sum;
}
};
int main()
{
Solution s;
int n = 0;
cin >> n;
cout << s.SumNum(n) << endl;;
return 0;
}
动态规划—递推思想
先举一个例子:
以4为例子来进行说明
4后面可以跟上1,2组成14,24
14后面跟不了,24可以跟上1组成124
再加上4本身就可以得到4的种类
即 14,24,124,4
而我们只要算出1,2的种类就可以加起来得到4的种类
因此,我们得到:
f[1]=1
f[2]=2=f[1]+1
f[3]=2=f[1]+1
f[4]=4=f[1]+f[2]+1
f[5]=4=f[1]+f[2]+1
当然这里dp[1]也可以不作为最优子结构,把dp[0]作为最优子结构,即dp[1]=dp[0]+1=1;
dp[0]=0;
通过上面的举例也可以得到dp[i]的含义,即当前数字i可以分解得到的所有组合数
由此得到状态转移方程:dp[i]=dp[1]+dp[2]+…+dp[n]+1; (n<=i/2)
这里的dp数组初始化情况就是当前i=0时,dp[0]=0,显然数字0分解不了,因此组合数为0
代码:
#include<iostream>
using namespace std;
#include<vector>
class Solution {
public:
int SumNum(int num)
{
vector<int> dp(num+1,0);
dp[0]=0;
for (int i = 1; i <=num; i++)
{
for (int j = 0;j <=i / 2; j++)
dp[i] += dp[j];
dp[i]++;
}
return dp[num];
}
};
int main()
{
Solution s;
int n = 0;
cin >> n;
cout << s.SumNum(n) << endl;;
return 0;
}
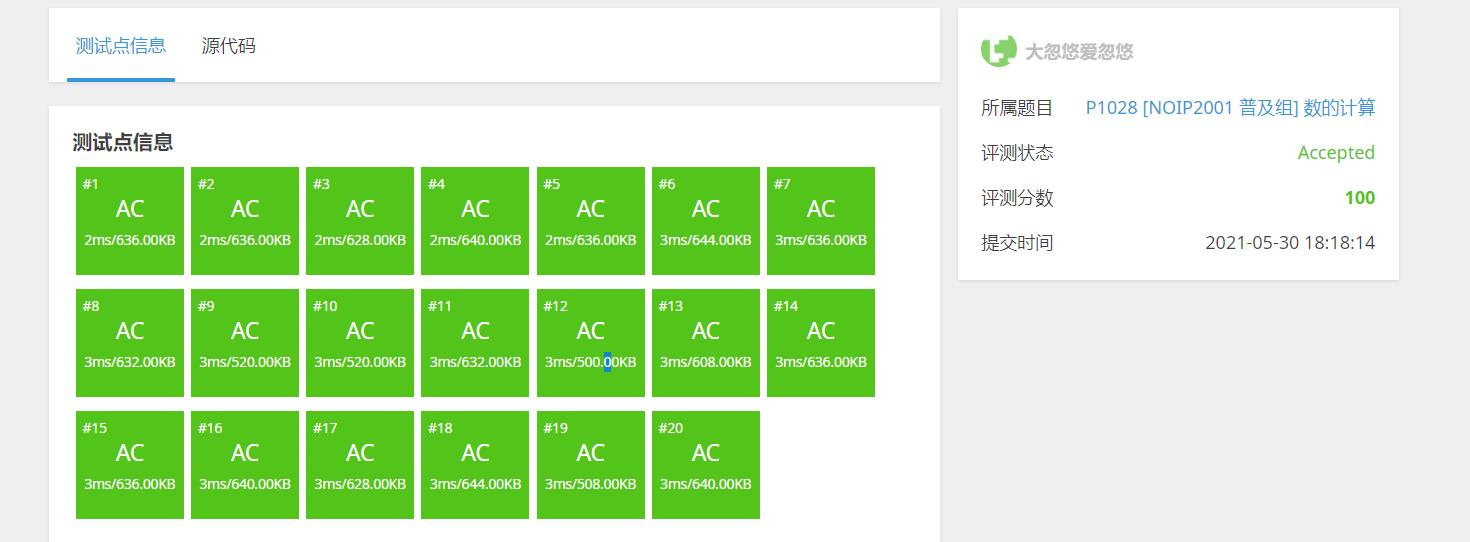
以上是关于DFS+记忆化剪枝--[NOIP2017 普及组] 棋盘的主要内容,如果未能解决你的问题,请参考以下文章
Party BFS搜索最长路径 + 记忆化剪枝 || dfs(逆向思维找父亲)
洛谷 P3953 [NOIP2017 提高组] 逛公园(最短路,记忆化搜索)
poj3373--Changing Digits(DFS+剪枝///记忆化)