2.Paper小结——《Privacy-preserving blockchain-based federated learning for traffic flow prediction》
Posted DK_521
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了2.Paper小结——《Privacy-preserving blockchain-based federated learning for traffic flow prediction》相关的知识,希望对你有一定的参考价值。
题目:
基于区块链的基于隐私保护的交通流量预测的联邦学习
0.Abstract:
交通流量预测已成为智能交通系统的重要组成部分。然而,现有的基于集中式机器学习的交通流量预测方法需要收集原始数据以进行模型训练,这涉及到严重的隐私暴露风险。为了解决这些问题,共享模型更新而不交换原始数据的联邦学习最近被引入,作为实现隐私保护的有效解决方案。然而,现有的联邦学习框架是基于一个集中的模型协调器,它仍然面临着严重的安全挑战,例如单点故障。因此,提出了一个基于区块链的联盟联邦学习框架,以在没有集中模型协调器的情况下实现分散、可靠和安全的联邦学习。此外,为了进一步保护区块链上的模型隐私,此方案采用了一种具有噪声添加机制的差分隐私方法。
优点:
数值结果表明,该方案能够有效地防止数据中毒攻击,提高模型更新的隐私保护,从而实现安全、保护隐私的交通流量预测。
1.Introduction
随着智能交通系统(ITS)的快速发展和部署,交通流量预测(TFP)模块收集了大量的交通信息,该模块提供实时交通分析,根据从各种传感器收集到的历史交通数据来估计未来的状态。TFP的作用:有助于支持交通控制部门和交通政策,分配道路资源,缓解交通拥堵,提高交通效率,最终实现交通管理,保证驾驶安全。目前,深度学习已被广泛应用于TFP,以学习通用的流量流特征,提高预测性能。然而,深度学习算法通常需要车辆将包含敏感信息集中式训练。如果中央服务器受损,整个TFP系统都会遭受典型的单点故障攻击,这可能很容易导致车辆的严重隐私损失。
FL是一种新的机器学习范式,它鼓励参与者协作训练由中央服务器发布的全局共享模型。
---------------------------------------------------------------------------------------------------------------------------------
传统FL的训练过程:
(1)在全局模型训练的每次迭代中,每个参与者都接收到一个初始的全局模型,执行局部模型训练,并在不上传原始数据的情况下将局部模型更新提交给中心服务器(即梯度参数)。
(2)然后,中心服务器聚合所有的本地模型更新,以获得一个新的全局模型,然后发布该模型。
(3)上述全局模型训练过程不断迭代,直到收敛。
传统FL的缺点 & 挑战:
(1)传统的FL很大程度上依赖于中央服务器收集和管理本地模型更新的中央服务器,因此不能避免单个故障点的安全漏洞。
(2)如果恶意车辆上传错误或低质量的局部模型更新到中心服务器,算法的收敛性能下降,这进一步影响了TFP系统的结果。
---------------------------------------------------------------------------------------------------------------------------------
因此,严格需要一个周到的FL框架来保证该算法的准确性和可靠性,从而提高该FL在TFP系统中的应用性能,以促进该算法的流量管理和政策执行。
为了应对这些挑战,我们专注于区块链,并进一步研究区块链和FL的结合,以增强整个TFP系统的安全和隐私保护。区块链作为一种分散的分布式公共账本技术,采用共识机制来同步P2P网络的变化,而不依赖于任何集中的实体或第三方。由于区块链特点:分散化、不可改变、可追溯性和匿名性等,区块链已广泛应用于多个领域的。我们希望通过验证本地模型更新和从恶意车辆中删除不可靠的模型更新,利用该技术在TFP中安全有效地实现FL。同时,我们考虑使用分散的区块链而不是中心服务器来记录和管理所有的本地模型更新,并解决单个故障点问题。
在本文,我们介绍了应用来自的轻量级而高效的神经网络模型来处理时间序列流量数据,并为去中心化的TFP系统构建联盟区块链(the consortium blockchain)。区块链联盟被利用来雇佣有限数量的预先选定的矿工来维护分布式分类帐。与公共和私有区块链技术相比,联盟区块链因其适度的管理开销、显著的网络可伸缩性和较低的共识延迟而被广泛接受。以防范这些安全威胁,我们在一个基于区块链的联盟框架中实现了整个FL过程,特别是通过使用委托的实用拜占庭容错(dBFT,Practical Byzantine Fault Tolerance)来描述共识过程。此外,我们利用本地差异隐私技术和噪声增加机制,加强参与车辆通信过程中需要与其他车辆共享位置的车辆的位置隐私保护。最后,在真实数据集的基础上进行了大量的数值实验,证明了该方案的有效性和有效性,有助于交通管理部门和交警做出正确的交通控制决策。
本文的主要贡献总结如下:
(1)我们修改了GRU神经网络,成功地提出了一种基于FL的TFP方法。在这种方法中,参与的车辆使用其数据进行局部模型训练并共享局部模型更新,而不是直接传输单个数据,从而保护隐私。
(2)我们利用联盟区块链,以分散的方式推广FL对TFP的应用。参与车辆提交的本地模型更新将被验证,中心服务器将被一组受信任的共识节点取代,以管理所有的本地模型更新。因此,防止了中心服务器和参与者方面的安全风险。
(3)我们应用本地差异隐私技术,为参与活动的车辆提供位置隐私保护。当参与的车辆上传其局部模型更新时,增加了高斯噪声(Gaussian noise)来干扰位置信息,最终防止违法者使用成员推理攻击从参与者那里收集信息。
第2节:相关文献。
第3节:基于TFP的GRU的FL。
第4节:基于fl的TFP的联盟区块链。
第5节:联盟区块链的共识算法设计
第6节:一种局部差异隐私技术被应用于TFP中的隐私保护车辆通信。
第7节:提出选择一个基于真实数据集的性能评估作为研究案例的框架。
第8节:一些结论和未来的工作。
2.Related Work
2.1 面向汽车互联网的TFP
TFP是ITS的一个重要组成部分,它直接影响交通的规划、管理和控制。考虑到TFP的实时预测,[J. Guo, W. Huang, B.M. Williams, Adaptive Kalman filter approach for stochastic short-term traffic flow rate prediction and uncertainty quantification, Transp. Res. C 43 (2014) 50–64.]采用季节性自回归综合移动平均线(SARIMA,the seasonal autoregressive integrated moving average)和广义自回归条件异方差(GARCH,generalized autoregressive conditional heteroscedasticity),并采用自适应卡尔曼滤波器(adaptive Kalman filters)实现。而[R. Yao, W. Zhang, L. Zhang, Hybrid methods for short-term traffic flow prediction based on arima-garch model and wavelet neural network, J. Transp. Eng. Part A Syst. 146 (2020) 04020086. ]的作者不仅应用SARIMA+GARCH预测常规部分,而且采用非线性方法预测不常规部分,有效地改善了TFP的结果。然而,上述方法是基于建立准确的TFP模型的建立,这在现实生活中很少实现。
随着人工智能的发展,在没有精确模型的情况下训练数据以获得近似模型的机器学习被成功地应用于TFP。长期短期记忆(LSTM)神经网络作为一种流行的机器学习算法,在TFP中可以有效地工作。随着自动编码器的附加特征提取能力,在[W. Wei, H. Wu, H. Ma, An autoencoder and lstm-based traffic flow prediction method, Sensors 19 (2946) (2019).]中提出了一种自动编码器LSTM。此外,[F. Zhao, G. Zeng, K. Lu, Enlstm-wpeo: Short-term traffic flow prediction by ensemble lstm, nnct weight integration, and population extremal optimization, IEEE Trans. Veh. Technol. 69 (2020) 101–113. ]的作者提出了一种杂交LSTM,并将短期TFP分为两个阶段。首先,采用五种LSTM来预测不同时间滞后条件下的交通流量。然后,无负约束理论或种群极值优化方法,对第一阶段得到的5个模型进行聚合,得到最终的TFP结果。除LSTM外,近年来一些研究人员采用回归神经网络和生成对抗胶囊网络来实现TFP。利用同时过去和未来的交通信息,作者在[S. Zhao, Q. Zhao, Y. Bai, S. Li, A traffic flow prediction method based on road crossing vector coding and a bidirectional recursive neural network, Electronics 8 (1006) (2019).]提出了一个双向回归神经网络来预测交通流。为了解决区域外延TFP问题,[J. Li, H. Li, G. Cui, Y. Kang, Y.Z. Yang Hu, Gacnet: A generative adversarial capsule network for regional epitaxial traffic flow prediction, Comput. Mater. Contin. 64 (2020) 925–940.]的作者提出了一种基于中心区域流入和流出信息的生成性对抗性胶囊网络。
2.2 车辆互联网的隐私和安全保护
已提出的FL方案:
(1)a privacy-enhanced FL proposed in [M. Hao, H. Li, X. Luo, G. Xu, H. Yang, S. Liu, Efficient and privacy-enhanced federated learning for industrial artificial intelligence, IEEE Trans. Ind. Inf. 16 (2020) 6532–6542.]
(2)为了解决在移动系统中分布式训练数据不平衡导致的FL精度下降的问题,提出了一个自我平衡的FL模型:[M. Duan, D. Liu, X. Chen, R. Liu, Y. Tan, L. Liang, Self-balancing federated learning with global imbalanced data in mobile systems, IEEE Trans. Parallel Distrib. Syst. 32 (2021) 59–71. ]
(3)为了解决客户端和云服务器之间的高通信成本,提出了高效的FL模型:[C. Fang, Y. Guo, N. Wang, A. Ju, Highly efficient federated learning with strong privacy preservation in cloud computing, Comput. Secur. 96 (2020) 101889.]
(4)以提高FL的收敛效率,在FL的局部更新过程中采用了动量梯度下降:[W. Liu, L. Chen, Y. Chen, W. Zhang, Accelerating federated learning via momentum gradient descent, IEEE Trans. Parallel Distrib. Syst. 31 (2020) 1754–1766.]
FL面临的挑战:
(1)集中式机制容易受到单点故障的攻击;
(2)恶意车辆可能会将错误或低质量的本地模型更新上传到中央服务器。
为了克服这些挑战,研究人员使用了分散的区块链技术。区块链技术采用分散的服务和共识机制,验证参与者的数据,防止不可靠和不安全的数据上传。通过将区块链与FL结合,[Z. Li, J. Liu, J. Hao, H. Wang, M. Xian, CrowdSFL: A secure crowd computing framework based on blockchain and federated learning, Electronics 9 (773) (2020). ]的作者引入了一个众包框架,在众包实现过程中减少开销和提高安全性。通过进一步考虑雾计算中的通信、共识延迟和计算成本,[Y. Qu, L. Gao, T.H. Luan, Y. Xiang, S. Yu, B. Li, G. Zheng, Decentralized privacy using blockchain-enabled federated learning in fog computing, IEEE Internet Things J. 7 (2020) 5171–5183.]的作者分析了区块链启用的FL的延迟性能,并导出了最优的块生成率。此外,一些工作采用了具有噪声添加机制的差异隐私方法,进一步增强了参与车辆的位置隐私保护,防止了成员推理攻击。为了应对工业物联网的对手攻击,[P.C.M. Arachchige, P. Bertok, I. Khalil, D. Liu, S. Camtepe, M. Atiquzzaman, A trustworthy privacy preserving framework for machine learning in industrial iot systems, IEEE Trans. Ind. Inf. 16 (2020) 6092–6102.]的作者引入了一个框架,集成了差异隐私、FL、以太坊区块链和智能合同,以增强数据的隐私和可信度。与之前的工作不同,一个运用了差分隐私和区块链的FL框架,可以防止中毒和成员推理攻击,它被用来增强5G[Y. Liu, J. Peng, J. Kang, A.M. Iliyasu, D. Niyato, A.A.A. El-Latif, A secure federated learning framework for 5g networks, IEEE Wirel. Commun. 27 (2020) 24–31. ]的安全性。在这个用于5G网络[M.S. Hossain, G. Muhammad, A deep-tree-model-based radio resource distribution for 5g networks, IEEE Wirel. Commun. 27 (2020) 62–67.]的安全FL框架中,区块链技术的智能合约被用于防止恶意或不可靠的参与者发送虚假数据,而差异隐私技术被用于防止成员推理攻击。
虽然上述研究采用了许多隐私保护方法,但没有一种方法不能直接应用于TFP。本研究探讨了一个基于区块链的联盟FL框架,以保护TFP中共享的信息的隐私和安全性。
3. FL for TFP 在本节中,我们将介绍基于GRU神经网络的FL对TFP的应用。 3.1. Overview of FL FL是一个保护隐私的分布式机器学习框架,它允许一组参与者(如车辆和设备)基于其本地数据协作训练全局模型,而不是收集本地数据进行集中的模型训练。参与者的个人数据可能包含敏感信息,但仍保留在本地存储中,从而通过FL保护用户隐私。在全局模型训练的每次迭代中,每个参与者都使用初始化的全局模型执行局部模型训练任务,然后根据梯度或权重确定局部模型的更新,并将其提交给中心服务器进行参数聚合。接下来,我们将重点关注特定迭代t(t∈1,2,……,T)中的FL过程。总之,该过程包括以下三个阶段。 阶段1,初始化:参与者向中央服务器注册以参与此过程。中央服务器选择具有较强计算和通信能力的合适参与者来完成本地模型训练任务。然后中心服务器向每个参与者发送一个初始化的全局模型ω0。 阶段2,训练:参与者k(k∈1,2,……,K)通过让
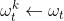 使用本地数据训练本地模型,并获得更新的本地模型
使用本地数据训练本地模型,并获得更新的本地模型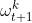 。换句话说,参与者试图通过处理损失函数的优化问题来训练局部模型,如下。
。换句话说,参与者试图通过处理损失函数的优化问题来训练局部模型,如下。
 阶段3,聚合:参与者将本地模型更新上传到中央服务器,该服务器使用一个典型的聚合算法,如FedSGD和FedAVG,来更新全局模型
阶段3,聚合:参与者将本地模型更新上传到中央服务器,该服务器使用一个典型的聚合算法,如FedSGD和FedAVG,来更新全局模型
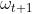 ,
,
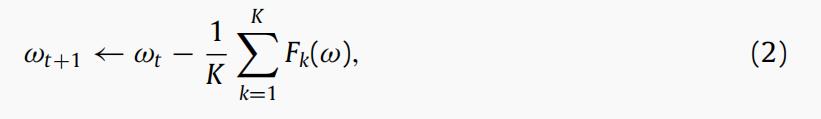 最后,中央服务器将新的全局模型ωt+1发送给每个参与者,进行下一次迭代。
3.2. FL-based TFP method using GRU
在本文中,我们旨在通过一个轻量级的FL方案来实现准确和及时的TFP。接下来,我们将GRU神经网络作为一种轻量级技术来预测未来的流量,并实现FL在TFP系统中的应用。GRU神经网络开发于2014年,已成为一种先进的序列预测模型,可以处理各种时间序列数据,包括交通流量和电力数据。
最后,中央服务器将新的全局模型ωt+1发送给每个参与者,进行下一次迭代。
3.2. FL-based TFP method using GRU
在本文中,我们旨在通过一个轻量级的FL方案来实现准确和及时的TFP。接下来,我们将GRU神经网络作为一种轻量级技术来预测未来的流量,并实现FL在TFP系统中的应用。GRU神经网络开发于2014年,已成为一种先进的序列预测模型,可以处理各种时间序列数据,包括交通流量和电力数据。
4.分散的TFP系统与FL
4.1. Threat model
在传统的FL中,参与者和中央服务器都有高度的自主权。参与者或中央服务器的故障会对FL的性能产生负面影响。接下来,我们从两个主要角度讨论安全威胁:服务器漏洞和参与者漏洞。首先,我们考虑了恶意中心服务器的安全风险,并总结如下。
(1)故障单点攻击:中央服务器是FL的一个重要的协调器,它可以收集和聚合所有的本地模型更新。如果中央服务器遭受典型的单点故障攻击,模型更新聚合的执行将失败,新的全局模型将不会分配给参与者进行后续的本地模型训练。这意味着整个FL算法将终止。
(2)成员推断攻击:由于中心服务器拥有来自所有参与者的关于本地模型更新的知识,因此中心服务器有机会记录参与者的本地模型的参数信息。中心服务器可以进一步利用本地模型的参数信息来执行成员资格推理攻击,以窃取参与者的本地数据集。在这种情况下,参与者不能知道他们的参数信息是否被中央服务器记录。这严重违反了FL的原则。
其次,恶意参与者可能会发起病毒攻击,以破坏全局模型训练的准确性。恶意参与者可以多种方式发动中毒攻击,总结如下。
(1)拜占庭攻击(Byzantine Attack):恶意参与者可以任意向中央服务器提供虚假或低质量的本地模型更新,而不是有效的本地模型更新,这将毒害服务器端全局模型训练 。因此,全局模型的精度将会急剧下降。
(2)标签翻转攻击(Label Flipping Attack):在GRU神经网络的执行过程中,恶意参与者可能会修改本地数据集的标签(即oVML模型学习的目标),以提供低质量的模型更新,从而影响整个学习阶段。例如,车辆可以在t时刻修改交通流量数据,这将影响该时刻交通流量的oVML预测(t+1)。
(3)数据病毒攻击(Data Poisoning Attack):参与者拥有本地训练数据集的所有权限,因此恶意参与者可能会添加极端的噪声,破坏本地数据集的质量,从而生成不可靠的本地模型更新。如果恶意参与者在中央服务器不知道的情况下,就很容易做到这一点。
上述攻击与本地模型更新有关。因此,我们需要检测恶意的本地模型更新,为FL在TFP系统中的应用提供安全和隐私保证。在本文中,我们使用区块链技术来执行模型更新验证任务,而无需使用第三方。
4.2. Consortium blockchain for FL-based TFP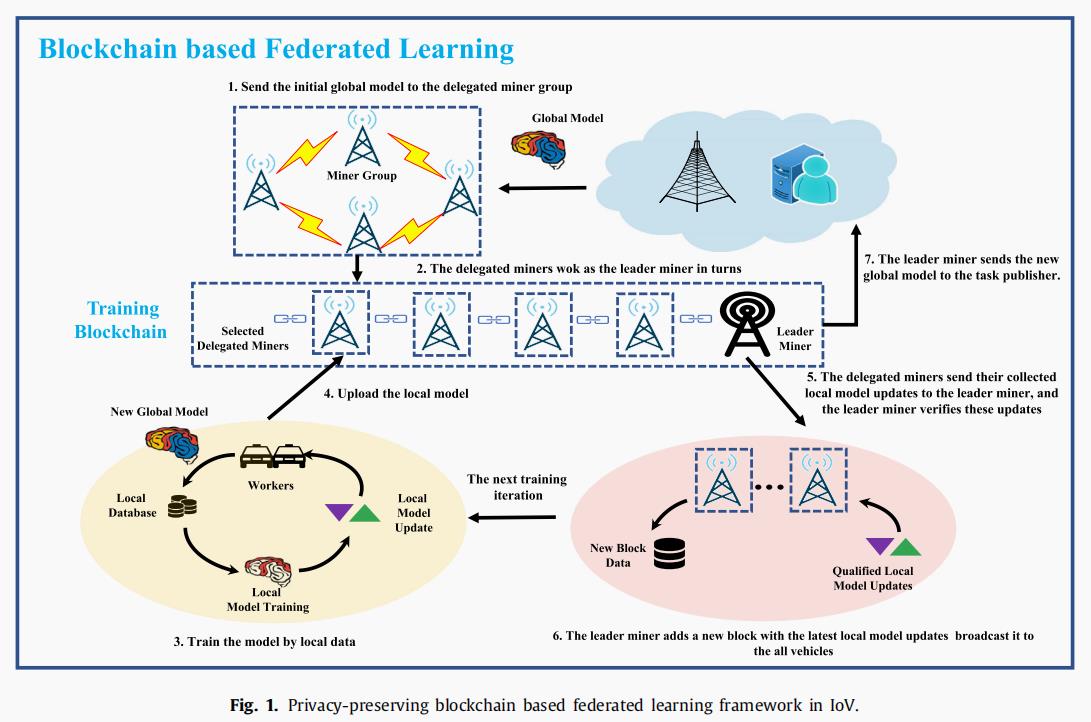 如图所示。1、建立了专门的联盟区块链,实现与FL分散的TFP系统。为了方便系统功能,我们首先选择一定数量的RSU作为授权矿工。为此,对这些RSU的硬件配置进行了升级,使它们具有强大的计算、存储和通信能力,以验证分布式车辆提交的本地模型更新,并识别低准确性和不可靠的更新。通过精心设计的共识算法,他们生成一个新的块,并记录合格的局部模型更新。随着联盟区块链的实现,FL对TFP应用中的全局模型训练的迭代包括以下阶段:
(1)本地模型训练:每辆车都使用其本地数据集执行GRU神经网络,以获得局部模型更新,并将这些更新发送给最近的矿工。
(2)模型更新验证:为了获得特定的代币奖励,我们使用矿工来接收和验证收集到的本地模型更新。当矿工使用一种有效的方法成功地过滤错误的和低质量的本地模型更新时,矿工将生成一个新的数据块来存储所有合格的本地模型更新。
(3)模型更新聚合:最后,由最新的本地模型更新组成的新块被记录在联盟区块链上,联盟区块链还负责通知所有参与者下载最新的块数据。每个参与者通过了解其他参与者的局部模型更新来进一步计算全局模型更新。
如图所示。1、建立了专门的联盟区块链,实现与FL分散的TFP系统。为了方便系统功能,我们首先选择一定数量的RSU作为授权矿工。为此,对这些RSU的硬件配置进行了升级,使它们具有强大的计算、存储和通信能力,以验证分布式车辆提交的本地模型更新,并识别低准确性和不可靠的更新。通过精心设计的共识算法,他们生成一个新的块,并记录合格的局部模型更新。随着联盟区块链的实现,FL对TFP应用中的全局模型训练的迭代包括以下阶段:
(1)本地模型训练:每辆车都使用其本地数据集执行GRU神经网络,以获得局部模型更新,并将这些更新发送给最近的矿工。
(2)模型更新验证:为了获得特定的代币奖励,我们使用矿工来接收和验证收集到的本地模型更新。当矿工使用一种有效的方法成功地过滤错误的和低质量的本地模型更新时,矿工将生成一个新的数据块来存储所有合格的本地模型更新。
(3)模型更新聚合:最后,由最新的本地模型更新组成的新块被记录在联盟区块链上,联盟区块链还负责通知所有参与者下载最新的块数据。每个参与者通过了解其他参与者的局部模型更新来进一步计算全局模型更新。
5.联盟区块链的共识算法设计
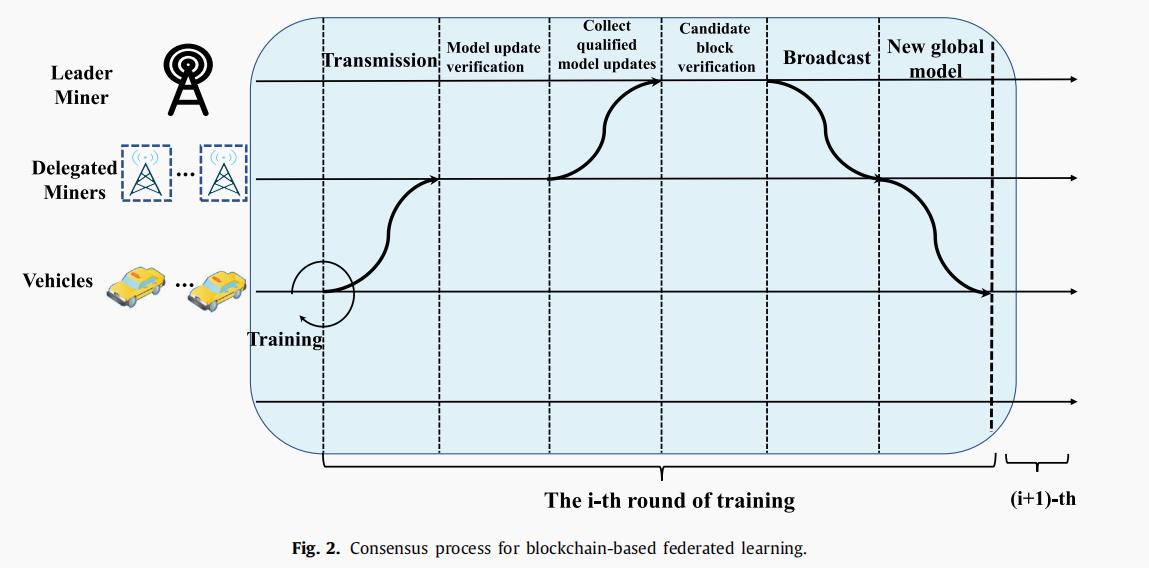
此外,如图所示。2、我们设计了一个有效的共识算法来抵御由恶意实体发起的安全攻击,例如,车辆或矿工。 每个矿工都被要求下载一个统一的测试数据集,并使用它来判断车辆上传的本地模型更新是否合格。根据算法精度的具体要求,每个矿机采用预定义的过滤策略来过滤有故障或中毒攻击的恶意实体。为了识别和纠正恶意实体对联盟区块链的不利影响,我们使用共识算法对恶意实体进行分析和过滤,即防止它们干扰正常的系统操作。我们利用共识算法的灵活性来抵御潜在的安全攻击。
更具体地说,采用一种名为dBFT的共识算法在矿工之间进行共识过程。只有合格的本地模型更新才会被聚合以生成最新的全局模型。通过这种方式,我们删除了低质量的本地模型更新,并最终实现了可靠的TFP。
与传统的共识算法,如计算密集型的工作证明、通信复杂的拜占庭容错和不公平的股权证明不同,dBFT是从实用的拜占庭容错演变而来的,并能够在没有固定矿工组的情况下灵活地改变矿工。与委托风险证明算法相比,dBFT在块数据的最终性方面具有更好的性能。受此启发,我们采用dBFT作为共识算法来建立一个高效和灵活的联盟区块链为FL在TFP中的应用。我们修改了共识过程,将模型更新验证集成到共识算法中,从而抵御任何潜在的安全攻击,并确保可靠的FL。关于协商一致过程的更多细节如下。
步骤1:初始化:选择了一组具有强大计算和通信能力的RSUs(Roadsides Units)作为候选矿工。一个全局信任权限,例如,一个政府部门,来认证这些矿工候选人的身份。只有合法的候选人可以被选择为被委托的矿工,并且受信任的当局接收他们的信息加密和数字签名证书。委托不仅生成或验证块数据,而且还基于给定的测试数据集执行模型更新验证任务。为了防止恶意委托,委托必须按照受信任权限的要求向特定帐户提交存款。所有代表均由其他代表监督。如果委托在共识过程中执行恶意行为,保证金将被没收,委托也将被列入黑名单并从委托组中删除。此外,将椭圆曲线数字签名算法和非对称密码算法应用于联盟区块链中作为安全保证。
步骤2:领导选择:与委托的股权证明类似,作为矿工工作的代表在dBFT中生成和验证块数据(如图1所示)。从代表中随机选择一名委托矿工(即一名代表)作为当前共识轮的领导矿工,其余代表在共识过程中充当追随者。我们认为联盟区块链中有N个最多g的恶意代表。为了确保区块链的安全性,我们假设在联盟区块链中 N>3g+1 才得到满足,领先者矿工每共识轮结束后发生变化。在N个时间段内,每个代表被随机选择为领导矿工,并给予一个回合来执行块轮流执行块生成、块广播、数据验证和块管理。
步骤3:本地模型训练:为了创建一个准确、及时的交通流量模型,提出了FL通过调度移动车辆执行算法1来训练全局模型。车辆协作地训练由TFP系统中的任务发布者发布的初始化全局模型,并迭代地生成它们自己的局部模型更新。然后,车辆在当前车辆通信技术的帮助下,使用自己的数字签名将这些局部模型更新上传到矿工组(即代表组)。
步骤4:模型更新验证:在收到本地模型更新后,矿工们首先通过验证发送者的数字签名和基于测试数据集估计本地模型更新的质量来验证发送者的合法性。为了实现可靠的模型更新,任务发布者提供的测试数据集可以是一个小的共享数据集,其中包含所有矿工的iid数据样本。该数据集被视为一个可靠的公共数据集来评估本地模型更新的质量。有了这个独特和通用的数据集,只有比给定阈值具有更高训练精度的合格本地模型更新才能被接受为发送给当前领先矿工的事务。此阈值由任务发布者根据应用程序要求确定。在测试数据集的帮助下,可以识别低质量的本地模型更新,并从模型更新聚合中删除。经过一段时间后,领导矿工收集合格的本地模型更新,生成一个具有其数字签名的新块,并将该块广播给其他作为追随者的矿工。追随者从领导矿工接收并验证块数据(包括先导矿器的签名、事务数据和所有事务的签名)。
步骤5:候选区块验证:候选块验证的过程包括以下步骤:
准备阶段:跟随者矿工为块数据生成验证结果,并将验证结果及其数字签名发送给对方,以便相互确认。当矿工收到对块数据的至少2g验证结果时,准备阶段已经完成。
提交阶段:每个追随者将它自己的验证结果与从其他追随者收到的结果进行比较,并回复一条确认消息,其中包括它对所有其他矿工的数字签名,以表明它是否同意验证结果。如果超过2g的+1矿工同意块数据,追随者将提交结果发送给一个数字签名给领导矿工,以证明大多数矿工同意块数据的真实性。
回复阶段:在收到来自不同追随者矿工的反馈后,领导矿工验证信息,并检查是否超过2/3的矿商对区块数据得出了相同的结论。如果是这样,块数据将被记录到联盟区块链中。
步骤6:全局模型训练:在FL中,所有参与者从联盟区块链下载新的区块块数据,并计算所有合格的本地模型更新的加权平均值作为他们新的全局模型。参与者利用新的全局模型作为初始化模型,进行下一次迭代的全局模型训练。当全球模型培训完成后,将记录持续提交合格的本地模型更新的车辆,并给予一定规模的金钱奖励。
在上述共识过程中,错误或低质量的局部模型更新没有集成到全局模型训练中,这提高了FL性能,减少了中毒攻击。因此,所提出的具有基于dBFT的共识算法的联盟区块链确保了基于fl的TFP方法的安全、可靠和隐私保护的特性。
6. Local differential privacy technique for privacy-preserving vehicular communications in TFP 与最初的差异隐私机制不同,自LDP机制侧重于在数据收集过程中保护参与者的隐私。LDP是一种有效的隐私保护对策,在局部干扰的帮助下广泛应用于分布式机器学习。设x为输入向量,通过随机算法M输出x的扰动向量
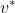 。因此,(ε,δ)-LDP可以定义如下:
。因此,(ε,δ)-LDP可以定义如下:
 根据定义1,参与者应该在数据中添加随机扰动。为了保护在TFP任务中车辆位置信息的隐私,我们通过应用
高斯机制添加了设计良好的噪声来干扰位置信息。我们首先对高斯机制的定义如下:
根据定义1,参与者应该在数据中添加随机扰动。为了保护在TFP任务中车辆位置信息的隐私,我们通过应用
高斯机制添加了设计良好的噪声来干扰位置信息。我们首先对高斯机制的定义如下:
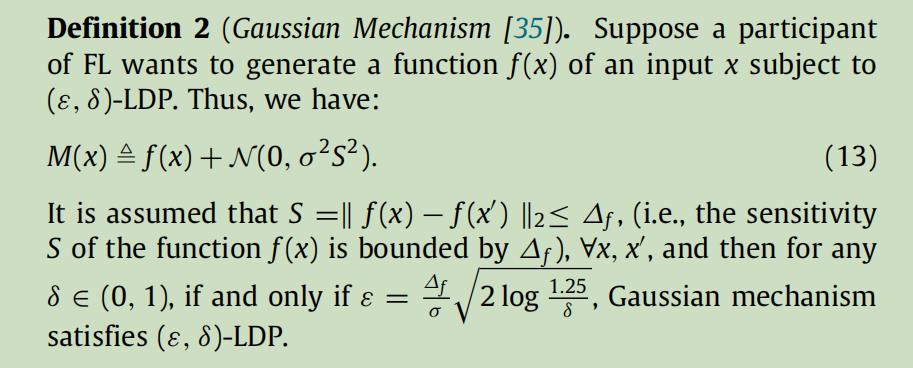
在本文中,我们假设车辆位置的经纬度坐标为(a、b)。当需要更新车辆的oVML时,车辆可能会与其他车辆共享其位置信息,这侵犯了位置隐私。因此,我们将LDP技术应用于上述程序,以支持车辆之间的隐私保护交互,如下。
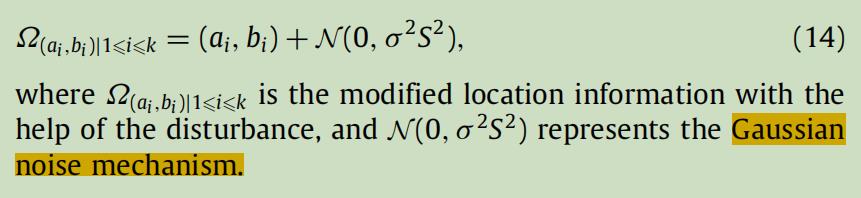
7. Experiments
后续更新
机器学习之爬山算法小结
简言
机器学习的项目,不可避免的需要补充一些优化算法,对于优化算法,爬山算法还是比较重要的.鉴于此,花了些时间仔细阅读了些爬山算法的paper.基于这些,做一些总结.
目录
1. 爬山算法简单描述
2. 爬山算法的主要算法
2.1 首选爬山算法
2.2 最陡爬山算法
2.3 随机重新开始爬山算法
2.4 模拟退火算法(也是爬山算法)
3. 实例求解
正文
爬山算法,是一种局部贪心的最优算法. 该算法的主要思想是:每次拿相邻点与当前点进行比对,取两者中较优者,作为爬坡的下一步.
举一个例子,求解下面表达式
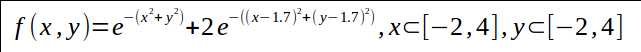 的最大值. 且假设 x,y均按为0.1间隔递增.
的最大值. 且假设 x,y均按为0.1间隔递增.
为了更好的描述,我们先使用pyhton画出该函数的图像:
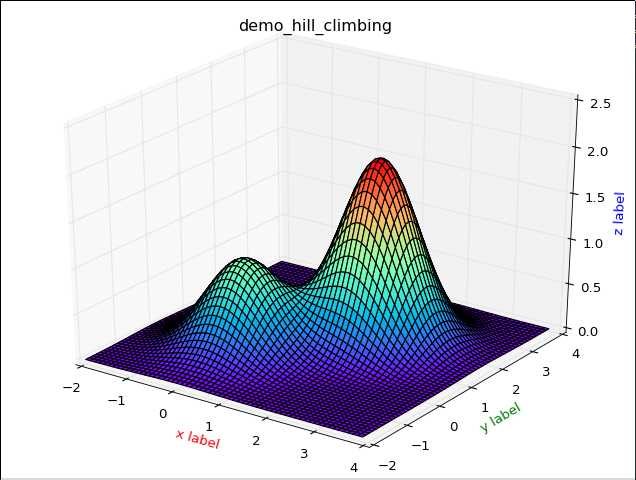
图像的python代码:

1 # encoding:utf8 2 from matplotlib import pyplot as plt 3 import numpy as np 4 from mpl_toolkits.mplot3d import Axes3D 5 6 7 def func(X, Y, x_move=0, y_move=0): 8 def mul(X, Y, alis=1): 9 return alis * np.exp(-(X * X + Y * Y)) 10 11 return mul(X, Y) + mul(X - x_move, Y - y_move, 2) 12 13 14 def show(X, Y): 15 fig = plt.figure() 16 ax = Axes3D(fig) 17 X, Y = np.meshgrid(X, Y) 18 Z = func(X, Y, 1.7, 1.7) 19 plt.title("demo_hill_climbing") 20 ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=‘rainbow‘, ) 21 ax.set_xlabel(‘x label‘, color=‘r‘) 22 ax.set_ylabel(‘y label‘, color=‘g‘) 23 ax.set_zlabel(‘z label‘, color=‘b‘) 24 # 具体函数方法可用 help(function) 查看,如:help(ax.plot_surface) 25 # ax.scatter(X,Y,Z,c=‘r‘) #绘点 26 plt.show() 27 28 if __name__ == ‘__main__‘: 29 X = np.arange(-2, 4, 0.1) 30 Y = np.arange(-2, 4, 0.1) 31 32 show(X,Y)
对于上面这个问题,我们使用爬山算法该如何求解呢? 下面我们从爬山算法中的几种方式分别求解一下这个小题.
1. 首选爬山算法
依次寻找该点X的邻近点中首次出现的比点X价值高的点,并将该点作为爬山的点(此处说的价值高,在该题中是指Z或f(x,y)值较大). 依次循环,直至该点的邻近点中不再有比其大的点. 我们成为该点就是山的顶点,又称为最优点.
那么解题思路就有:
1. 随机选择一个登山的起点S(x0,y0,z0),并以此为起点开始登山.直至"登顶".
下面是我们实现的代码:

1 # encoding:utf8 2 from random import random, randint 3 4 from matplotlib import pyplot as plt 5 import numpy as np 6 from mpl_toolkits.mplot3d import Axes3D 7 8 9 def func(X, Y, x_move=1.7, y_move=1.7): 10 def mul(X, Y, alis=1): 11 return alis * np.exp(-(X * X + Y * Y)) 12 13 return mul(X, Y) + mul(X - x_move, Y - y_move, 2) 14 15 16 def show(X, Y, Z): 17 fig = plt.figure() 18 ax = Axes3D(fig) 19 plt.title("demo_hill_climbing") 20 ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=‘rainbow‘, ) 21 ax.set_xlabel(‘x label‘, color=‘r‘) 22 ax.set_ylabel(‘y label‘, color=‘g‘) 23 ax.set_zlabel(‘z label‘, color=‘b‘) 24 # ax.scatter(X,Y,Z,c=‘r‘) #绘点 25 plt.show() 26 27 28 def drawPaht(X, Y, Z,px,py,pz): 29 fig = plt.figure() 30 ax = Axes3D(fig) 31 plt.title("demo_hill_climbing") 32 ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=‘rainbow‘, ) 33 ax.set_xlabel(‘x label‘, color=‘r‘) 34 ax.set_ylabel(‘y label‘, color=‘g‘) 35 ax.set_zlabel(‘z label‘, color=‘b‘) 36 ax.plot(px,py,pz,‘r.‘) #绘点 37 plt.show() 38 39 40 def hill_climb(X, Y): 41 global_X = [] 42 global_Y = [] 43 44 len_x = len(X) 45 len_y = len(Y) 46 # 随机登山点 47 st_x = randint(0, len_x-1) 48 st_y = randint(0, len_y-1) 49 50 def argmax(stx, sty, alisx=0, alisy=0): 51 cur = func(X[0][st_x], Y[st_y][0]) 52 next = func(X[0][st_x + alisx], Y[st_y + alisy][0]) 53 54 return cur < next and True or False 55 56 while (len_x > st_x >= 0) or (len_y > st_y >= 0): 57 if st_x + 1 < len_x and argmax(st_x, st_y, 1): 58 st_x += 1 59 elif st_y + 1 < len_x and argmax(st_x, st_y, 0, 1): 60 st_y += 1 61 elif st_x >= 1 and argmax(st_x, st_y, -1): 62 st_x -= 1 63 elif st_y >= 1 and argmax(st_x, st_y, 0, -1): 64 st_y -= 1 65 else: 66 break 67 global_X.append(X[0][st_x]) 68 global_Y.append(Y[st_y][0]) 69 return global_X, global_Y, func(X[0][st_x], Y[st_y][0]) 70 71 72 if __name__ == ‘__main__‘: 73 X = np.arange(-2, 4, 0.1) 74 Y = np.arange(-2, 4, 0.1) 75 X, Y = np.meshgrid(X, Y) 76 Z = func(X, Y, 1.7, 1.7) 77 px, py, maxhill = hill_climb(X, Y) 78 print px,py,maxhill 79 drawPaht(X, Y, Z,px,py,func(np.array(px), np.array(py), 1.7, 1.7))
对比几次运行的结果:
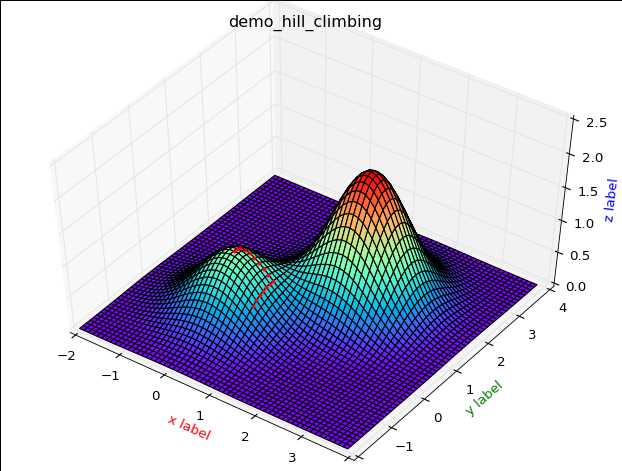
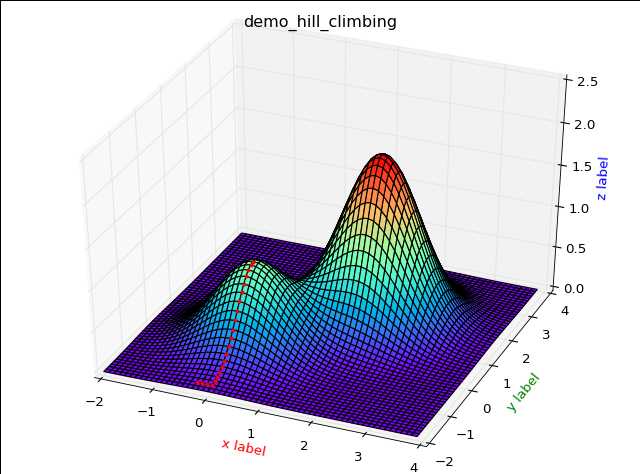
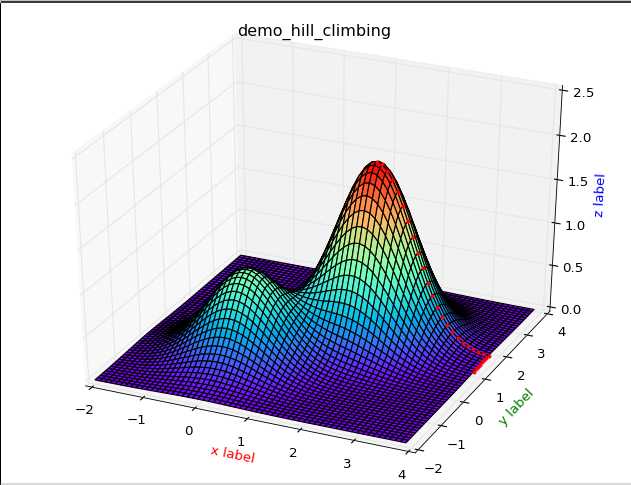
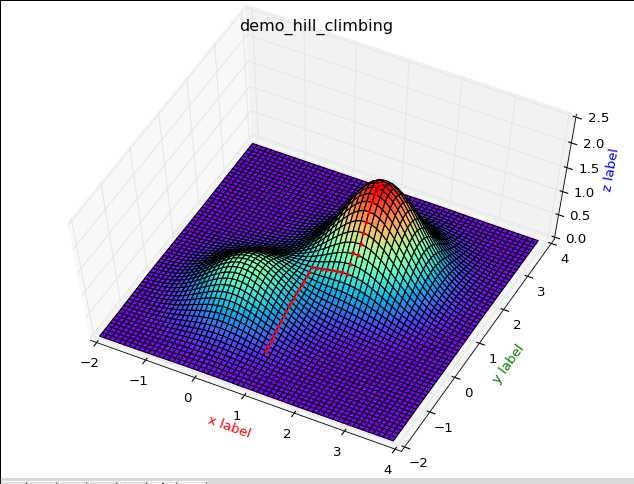
从上图中,我们可以比较清楚的观察到,首选爬山算法的缺陷.
2.那么最陡爬山算法呢?
简单描述:
最陡爬山算法是在首选爬山算法上的一种改良,它规定每次选取邻近点价值最大的那个点作为爬上的点.
下面我们来实现一下它:

1 # encoding:utf8 2 from random import random, randint 3 4 from matplotlib import pyplot as plt 5 import numpy as np 6 from mpl_toolkits.mplot3d import Axes3D 7 8 9 def func(X, Y, x_move=1.7, y_move=1.7): 10 def mul(X, Y, alis=1): 11 return alis * np.exp(-(X * X + Y * Y)) 12 13 return mul(X, Y) + mul(X - x_move, Y - y_move, 2) 14 15 16 def show(X, Y, Z): 17 fig = plt.figure() 18 ax = Axes3D(fig) 19 plt.title("demo_hill_climbing") 20 ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=‘rainbow‘, ) 21 ax.set_xlabel(‘x label‘, color=‘r‘) 22 ax.set_ylabel(‘y label‘, color=‘g‘) 23 ax.set_zlabel(‘z label‘, color=‘b‘) 24 # ax.scatter(X,Y,Z,c=‘r‘) #绘点 25 plt.show() 26 27 28 def drawPaht(X, Y, Z, px, py, pz): 29 fig = plt.figure() 30 ax = Axes3D(fig) 31 plt.title("demo_hill_climbing") 32 ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=‘rainbow‘, ) 33 ax.set_xlabel(‘x label‘, color=‘r‘) 34 ax.set_ylabel(‘y label‘, color=‘g‘) 35 ax.set_zlabel(‘z label‘, color=‘b‘) 36 ax.plot(px, py, pz, ‘r.‘) # 绘点 37 plt.show() 38 39 40 def hill_climb(X, Y): 41 global_X = [] 42 global_Y = [] 43 44 len_x = len(X) 45 len_y = len(Y) 46 # 随机登山点 47 st_x = randint(0, len_x - 1) 48 st_y = randint(0, len_y - 1) 49 50 def argmax(stx, sty, alisx, alisy): 51 cur = func(X[0][stx], Y[sty][0]) 52 next = func(X[0][alisx], Y[alisy][0]) 53 if cur < next: 54 return alisx, alisy 55 return stx, sty 56 #return cur < next and alisx, alisy or stx, sty 57 58 tmp_x = st_x 59 tmp_y = st_y 60 while (len_x > st_x >= 0) or (len_y > st_y >= 0): 61 if st_x + 1 < len_x: 62 tmp_x, tmp_y = argmax(tmp_x, tmp_y, (st_x + 1), st_y) 63 64 if st_x >= 1: 65 tmp_x, tmp_y = argmax(tmp_x, tmp_y, st_x - 1, st_y) 66 67 if st_y + 1 < len_x: 68 tmp_x, tmp_y = argmax(tmp_x, tmp_y, st_x, st_y + 1) 69 70 if st_y >= 1: 71 tmp_x, tmp_y = argmax(tmp_x, tmp_y, st_x, st_y - 1) 72 73 if tmp_x != st_x or tmp_y != st_y: 74 st_x = tmp_x 75 st_y = tmp_y 76 else: 77 break 78 global_X.append(X[0][st_x]) 79 global_Y.append(Y[st_y][0]) 80 return global_X, global_Y, func(X[0][st_x], Y[st_y][0]) 81 82 83 if __name__ == ‘__main__‘: 84 X = np.arange(-2, 4, 0.1) 85 Y = np.arange(-2, 4, 0.1) 86 X, Y = np.meshgrid(X, Y) 87 Z = func(X, Y, 1.7, 1.7) 88 px, py, maxhill = hill_climb(X, Y) 89 print px, py, maxhill 90 drawPaht(X, Y, Z, px, py, func(np.array(px), np.array(py), 1.7, 1.7))
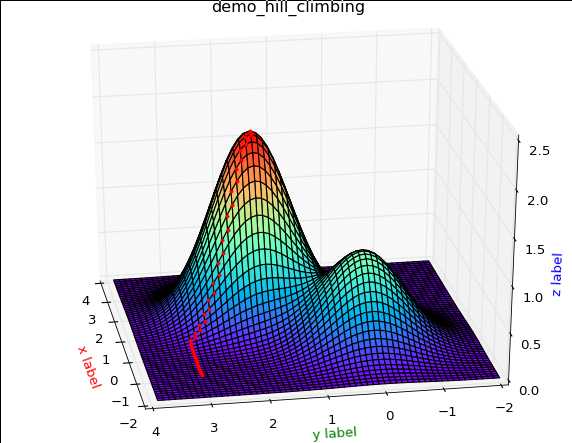
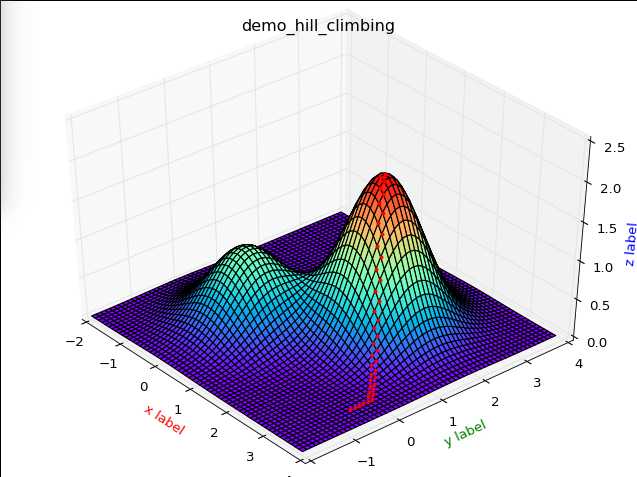
从这个结果来看,因为范围扩大了一点,所以效果会好一点点,当依旧是一个局部最优算法.
3.随机重新开始爬山算法呢?
简单的描述:
随机重新开始爬山算法是基于最陡爬山算法,其实就是加一个达到全局最优解的条件,如果满足该条件,就结束运算,反之则无限次重复运算最陡爬山算法.
由于此题,并没有结束的特征条件,我们这里就不给予实现.
4.
以上是关于2.Paper小结——《Privacy-preserving blockchain-based federated learning for traffic flow prediction》的主要内容,如果未能解决你的问题,请参考以下文章
