最短路径之迪杰斯特拉算法的Java实现

Posted 2020-10-10 心中的山水

　　Dijkstra算法是最短路径算法中为人熟知的一种，是单起点全路径算法。该算法被称为是“贪心算法”的成功典范。本文接下来将尝试以最通俗的语言来介绍这个伟大的算法，并赋予java实现代码。

一、知识准备

1、表示图的数据结构

　　用于存储图的数据结构有多种，本算法中笔者使用的是邻接矩阵。

 　 图的邻接矩阵存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组（邻接矩阵）存储图中的边或弧的信息。

  设图G有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

　　

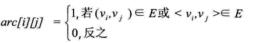
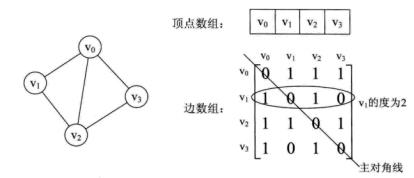
从上面可以看出，无向图的边数组是一个对称矩阵。所谓对称矩阵就是n阶矩阵的元满足a_ij = a_ji。即从矩阵的左上角到右下角的主对角线为轴，右上角的元和左下角相对应的元全都是相等的。

    从这个矩阵中，很容易知道图中的信息。

    （1）要判断任意两顶点是否有边无边就很容易了；

    （2）要知道某个顶点的度，其实就是这个顶点vi在邻接矩阵中第i行或（第i列）的元素之和；

    （3）求顶点vi的所有邻接点就是将矩阵中第i行元素扫描一遍，arc[i][j]为1就是邻接点；

    而有向图讲究入度和出度，顶点vi的入度为1，正好是第i列各数之和。顶点vi的出度为2，即第i行的各数之和。

　　有向图的定义也类似，故不做赘述。

2、单起点全路径

　　　　所谓单起点全路径，就是指在一个图中，从一个起点出发，到所有节点的最短路径。

 

3、图论的基本知识(读者需自行寻找相关资料)

 

4、互补松弛条件

　设标量d1,d2,....,dN满足

　　　　dj<=di + aij,  (i,j)属于A,

　且P是以i1为起点ik为终点的路，如果

　　　　dj = di + aij, 对P的所有边(i, j)

　成立，那么P是从i1到ik的最短路。其中，满足上面两式的被称为最短路问题的互补松弛条件。

二、算法思想

1、令G = （V，E）为一个带权无向图。G中若有两个相邻的节点,i和j。aij(在这及其后面都表示为下标，请注意)为节点i到节点j的权值，在本算法可以理解为距离。每个节点都有一个值di(节点标记)表示其从起点到它的某条路的距离。

　　2、算法初始有一个数组V用于储存未访问节点的列表，我们暂称为候选列表。选定节点1为起始节点。开始时，节点1的d1=0, 其他节点di=无穷大，V为所有节点。
初始化条件后，然后开始迭代算法，直到V为空集时停止。具体迭代步骤如下：

　　 将d值最小的节点di从候选列表中移除。(本例中V的数据结构采用的是优先队列实现最小值出列，最好使用斐波那契对，在以前文章有过介绍，性能有大幅提示)。对于以该节点为起点的每一条边，不包括移除V的节点, (i, j)属于A， 若dj > di + aij（违反松弛条件）,则令

　　dj = di + aij    , （如果j已经从V中移除过，说明其最小距离已经计算出，不参与此次计算）

　　可以看到在算法的运算工程中，节点的d值是单调不增的

　　具体算法图解如下

　　

三、代码实现

//接受一个有向图的权重矩阵，和一个起点编号start（从0编号，顶点存在数组中)
	//返回一个int[] 数组，表示从start到它的最短路径长度  
	public static int[] Dijsktra(int[][]weight,int start){
		int length = weight.length;
		int[] shortPath = new int[length];//存放从start到各个点的最短距离
		shortPath[0] = 0;//start到他本身的距离最短为0
		String path[] = new String[length];//存放从start点到各点的最短路径的字符串表示
		for(int i=0;i<length;i++){
			path[i] = start+"->"+i;
		}
		int visited[] = new int[length];//标记当前该顶点的最短路径是否已经求出，1表示已经求出
		visited[0] = 1;//start点的最短距离已经求出
		for(int count = 1;count<length;count++){
			int k=-1;
			int dmin = Integer.MAX_VALUE;
			for(int i=0;i<length;i++){
				if(visited[i]==0 && weight[start][i]<dmin){
					dmin = weight[start][i];
					k=i;
				}
			}
			//选出一个距离start最近的未标记的顶点     将新选出的顶点标记为以求出最短路径，且到start的最短路径为dmin。
			shortPath[k] = dmin;
			visited[k] = 1;
			//以k为中间点，修正从start到未访问各点的距离
			for(int i=0;i<length;i++){
				if(visited[i]==0 && weight[start][k]+weight[k][i]<weight[start][i]){
					weight[start][i] = weight[start][k]+weight[k][i];
					path[i] = path[k]+"->"+i;
				}
			}
		}
		for(int i=0;i<length;i++){
			System.out.println("从"+start+"出发到"+i+"的最短路径为："+path[i]+"="+shortPath[i]);
		}
		return shortPath;
		
	}

　　这便是利用迪杰斯特拉算法实现最短路径的方法。

之后可以声明一个常量，例如：

static final int MAX = 10000;

然后在main方法里面建一个邻接矩阵，调用此方法即可。

public static void main(String[] args) {
		int[][] weight = {
				{0,3,2000,7,MAX},
				{3,0,4,2,MAX},
				{MAX,4,0,5,4},
				{7,2,5,0,6},
				{MAX,MAX,4,6,0}
				};
		int start = 0;
		int[] dijsktra = Dijsktra(weight,start);
	}

　　参考自：http://www.cnblogs.com/junyuhuang/p/4544747.html