Python数据结构与算法篇-- 二分查找与二分答案

Posted 长路漫漫2021

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了Python数据结构与算法篇-- 二分查找与二分答案相关的知识，希望对你有一定的参考价值。

1 二分法介绍

1.1 定义

        二分查找又称折半查找、二分搜索、折半搜索等，是一种在静态查找表中查找特定元素的算法。

        所谓静态查找表，即只能对表内的元素做查找和读取操作，不允许插入或删除元素。

        使用二分查找算法，必须保证查找表中存放的是有序序列（升序或者降序）。换句话说，存储无序序列的静态查找表，除非先对数据进行排序，否则不能使用二分查找算法。它针对的是一个有序的数据集合，查找思想有点类似分治思想。每次都通过跟区间的中间元素对比，将待查找的区间缩小为之前的一半，直到找到要查找的元素，或者区间被缩小为 0。下图对比了顺序查找和二分查找的不同：

        二分查找的最基本问题是在有序数组里查找一个特定的元素，还可以应用在：

  1. 在半有序（旋转有序或者是山脉）数组里查找元素；
  2. 确定一个有范围的整数；
  3. 需要查找的目标元素满足某个特定的性质。

        二分查找算法的时间复杂度可以用 O ( l o g 2 n ) O(log_2n) O(log2​n) 表示（ n n n 为查找表中的元素数量，底数 2 可以省略）。和顺序查找算法的 O ( n ) O(n) O(n) 相比，显然二分查找算法的效率更高，且查找表中的元素越多，二分查找算法效率高的优势就越明显。

1.2 二分法的三种写法

1. 模板一

class Solution(object):

    def search(self, nums: List[int], target: int) -> int:
        # 特殊用例判断
        n = len(nums)
        if n == 0:
            return -1
        # 在 [left, right] 区间里查找target
        left, right = 0, n - 1
        while left <= right:
            # 为了防止 left + right 整形溢出，写成如下形式
            # Python 使用 BigInteger，所以不用担心溢出，但还是推荐使用如下方式
            mid = left + (right - left) // 2

            if nums[mid] == target:
                return mid
            elif nums[mid] > target:
                # 下一轮搜索区间：[left, mid - 1]
                right = mid - 1
            else:
                # 此时：nums[mid] < target
                # 下一轮搜索区间：[mid + 1, right]
                left = mid + 1
        return -1

注意事项：

  • 许多刚刚写的朋友，经常在写 left = mid + 1；还是写 right = mid - 1; 感到困惑，一个行之有效的思考策略是：永远去想下一轮目标元素应该在哪个区间里：
    • 如果目标元素在区间 [left, mid - 1] 里，就需要设置设置 right = mid - 1；
    • 如果目标元素在区间 [mid + 1, right] 里，就需要设置设置 left = mid + 1；

        考虑不仔细是初学二分法容易出错的地方，这里切忌跳步，需要仔细想清楚每一行代码的含义。

  • 二分查找算法是典型的「减治思想」的应用，我们使用二分查找将待搜索的区间逐渐缩小，以达到「缩减问题规模」的目的；
  • 循环可以继续的条件是 while (left <= right)，特别地，当 left == right 即当待搜索区间里只有一个元素的时候，查找也必须进行下去；
  • mid = (left + right) // 2；在 left + right 整形溢出的时候，mid 会变成负数，回避这个问题的办法是写成 mid = left + (right - left) // 2。

2. 模板二

版本一：

def search(nums: List[int], left: int, right: int, target: int) -> int:
    while left < right:
        # 选择中位数时下取整
        mid = left + (right - left) // 2
        if check(mid):
            # 下一轮搜索区间是 [mid + 1, right]
            left = mid + 1
        else:
            # 下一轮搜索区间是 [left, mid]
            right = mid
    # 退出循环的时候，程序只剩下一个元素没有看到。
    # 视情况，是否需要单独判断 left（或者 right）这个下标的元素是否符合题意

版本二：

def search(nums: List[int], left: int, right: int, target: int) -> int:
    while left < right:
        # 选择中位数时上取整
        mid = left + (right - left + 1) // 2
        if check(mid):
            # 下一轮搜索区间是 [left, mid - 1]
            right = mid - 1
        else:
            # 下一轮搜索区间是 [mid, right]
            left = mid
    # 退出循环的时候，程序只剩下一个元素没有看到。
    # 视情况，是否需要单独判断 left（或者 right）这个下标的元素是否符合题意

理解模板代码的要点：

  • 核心思想：虽然模板有两个，但是核心思想只有一个，那就是：把待搜索的目标元素放在最后判断，每一次循环排除掉不存在目标元素的区间，目的依然是确定下一轮搜索的区间；
  • 特征：while (left < right):，这里使用严格小于 < 表示的临界条件是：当区间里的元素只有 2 个时，依然可以执行循环体。换句话说，退出循环的时候一定有 left == right成立，这一点在定位元素下标的时候极其有用；
  • 在循环体中，先考虑 nums[mid] 在满足什么条件下不是目标元素，进而考虑两个区间 [left, mid - 1] 以及 [mid + 1, right] 里元素的性质，目的依然是确定下一轮搜索的区间； 注意 1： 先考虑什么时候不是解，是一个经验，在绝大多数情况下不易出错，重点还是确定下一轮搜索的区间，由于这一步不容易出错，它的反面（也就是 else 语句的部分），就不用去考虑对应的区间是什么，直接从上一个分支的反面区间得到，进而确定边界如何设置；
  • 根据边界情况，看取中间数的时候是否需要上取整； 注意 2： 这一步也依然是根据经验，建议先不要记住结论，在使用这个思想解决问题的过程中，去思考可能产生死循环的原因，进而理解什么时候需要在括号里加 1 ，什么时候不需要；
  • 在退出循环以后，根据情况看是否需要对下标为 left 或者 right 的元素进行单独判断，这一步叫「后处理」。在有些问题中，排除掉所有不符合要求的元素以后，剩下的那 1 个元素就一定是目标元素。如果根据问题的场景，目标元素一定在搜索区间里，那么退出循环以后，可以直接返回 left（或者 right）。

        以上是这两个模板写法的所有要点，并且是高度概括的。请读者一定先抓住这个模板的核心思想，在具体使用的过程中，不断地去体会这个模板使用的细节和好处。只要把中间最难理解的部分吃透，几乎所有的二分问题就都可以使用这个模板来解决，因为「减治思想」是通用的。好处在这一小节的开篇介绍过了，需要考虑的细节最少。

        学习建议：一定需要多做练习，体会这（两）个模板的使用。

注意事项：

  • 先写分支，再决定中间数是否上取整；
  • 在使用多了以后，就很容易记住，只要看到 left = mid ，它对应的取中位数的取法一定是 mid = left + (right - left + 1) // 2。

3. 模板三

def search(nums: List[int], left: int, right: int, target: int) -> int:
    while left + 1 < right:
        # 选择中位数时下取整
        mid = left + (right - left) // 2
        if nums[mid] == target:
            return mid
        elif nums[mid] < target:
            left = mid
        else:
            right = mid

    if nums[left] == target:
        return left
    if nums[right] == target:
        return right
    return -1
  • 这一版代码和模板二没有本质区别，一个显著的标志是：循环可以继续的条件是 while (left + 1 < right):，这说明在退出循环的时候，一定有 left + 1 == right 成立，也就是退出循环以后，区间有 2 个元素，即 [left, right]；
  • 这种写法的优点是：不用理解上一个版本在分支出现 left = mid 的时候中间数上取整的行为；
  • 缺点是显而易见的：
    • while (left + 1 < right): 写法相对于 while (left < right): 和 while (left <= right): 来说并不自然；
    • 由于退出循环以后，区间一定有两个元素，需要思考哪一个元素才是需要找的，即「后处理」一定要做，有些时候还会有先考虑 left 还是 right 的区别。

小结：

  • 模板一：最好理解的版本，但是在刷题的过程中，需要处理一些边界的问题，一不小心容易出错；
  • 模板二：强烈推荐掌握的版本，应先理解思想，再通过实际应用去体会这个模板的细节，熟练使用以后就会觉得非常自然；
  • 模板三：可以认为是模板二的避免踩坑版本，只要深刻理解了模板二，模板三就不在话下。

         实际应用中，选择最好理解的版本即可。

        这里有一个提示：模板二考虑的细节最少，可以用于解决一些相对复杂的问题。缺点是：学习成本较高，初学的时候比较容易陷入死循环，建议大家通过多多使用，并且尝试 debug，找到死循环的原因，进而掌握。

        题解核心内容：所有模板都一样，不可以套模板，而应该仔细看题（解题的关键在认真读题），分析清楚题目要找的答案需要满足什么性质。采用两边夹的方式，每一轮把待搜索区间分成两个部分，排除掉一定不是答案的区间，最后左右指针重合的地方就是我们要找的元素。一定要分析清楚题目的意思，分析清楚要找的答案需要满足什么性质。应该清楚模板具体的用法，明白需要根据题意灵活处理、需要变通的地方，不可以认为每一行代码都是模板规定死的写法，不可以盲目套用、死记硬背。

2 常见题型

2.1 二分求下标（在数组中查找符合条件的元素的下标）

题库列表

题号链接
704二分查找（简单）
35搜索插入位置（简单）
300最长上升子序列（中等）
34在排序数组中查找元素的第一个和最后一个位置（简单）
611有效三角形的个数
436寻找右区间（中等）
4寻找两个有序数组的中位数（困难）

2.2 完全有序

704. 二分查找
        题目描述：给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

# lower_bound 返回最小的满足 nums[i] >= target 的 i
# 如果数组为空，或者所有数都 < target，则返回 len(nums)
# 要求 nums 是非递减的，即 nums[i] <= nums[i + 1]

# 闭区间写法
def lower_bound(nums: List[int], target: int) -> int:
    left, right = 0, len(nums) - 1  # 闭区间 [left, right]
    while left <= right:  # 区间不为空
        # 循环不变量：
        # nums[left-1] < target
        # nums[right+1] >= target
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid + 1      # 范围缩小到 [mid+1, right]
        else:
            right = mid - 1     # 范围缩小到 [left, mid-1]
    return left                 # 或者 right+1

# 左闭右开区间写法
def lower_bound2(nums: List[int], target: int) -> int:
    left, right = 0, len(nums)  # 左闭右开区间 [left, right)
    while left < right:  # 区间不为空
        # 循环不变量：
        # nums[left-1] < target
        # nums[right] >= target
        mid = (left + right) // 2
        if nums[mid] < target:
            left = mid + 1  # 范围缩小到 [mid+1, right)
        else:
            right = mid  # 范围缩小到 [left, mid)
    return left  # 或者 right

# 开区间写法
def lower_bound3(nums: List[int], target: int) -> int:
    left, right = -1, len(nums)  # 开区间 (left, right)
    while left + 1 < right:  # 区间不为空
        mid = (left + right) // 2
        # 循环不变量：
        # nums[left] < target
        # nums[right] >= target
        if nums[mid] < target:
            left = mid  # 范围缩小到 (mid, right)
        else:
            right = mid  # 范围缩小到 (left, mid)
    return right  # 或者 left+1

class Solution:
    def search(self, nums: List[int], target: int) -> int:
        i = lower_bound(nums, target)  # 选择其中一种写法即可
        return i if i < len(nums) and nums[i] == target else -1

35. 搜索插入位置

        题目描述：给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums) - 1
        while left <= right:
            mid = (left + right) // 2
            if nums[mid] == target:
                return mid
            elif nums[mid] < target:
                left = mid + 1
            else:
                right = mid - 1
        return left

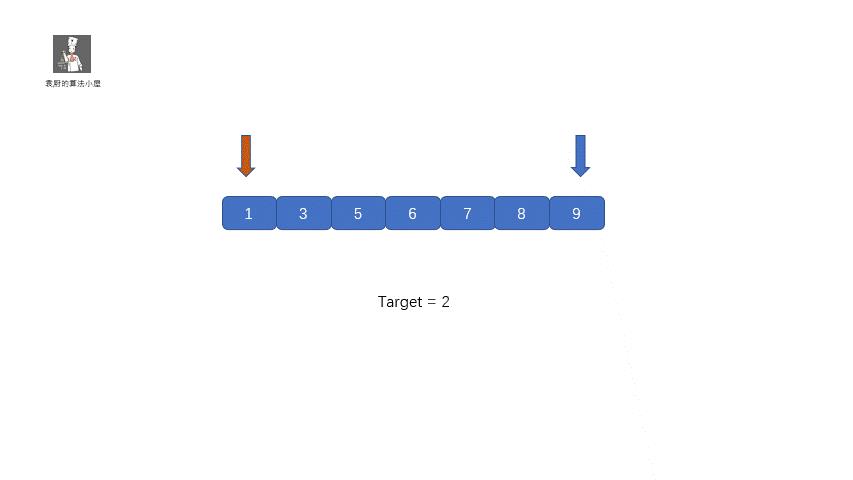
class Solution:
    def searchInsert(self, nums: List[int], target: int) -> int:
        left, right = 0, len(nums)          # 采用左闭右开区间[left,right)
        while left < right:                 # 右开所以不能有=,区间不存在
            mid = left + (right - left)//2  # 防止溢出, //表示整除
            if nums[mid] < target:          # 中点小于目标值,在右侧,可以得到相等位置
                left = mid + 1              # 左闭, 所以要+1
            else:
                right = mid                 # 右开, 真正右端点为mid-1
        return left                         # 此算法结束时保证left = right, 返回谁都一样

300. 最长上升子序列
        题目描述：给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

1. 动态规划 + 二分查找

# Dynamic programming + Dichotomy.
class Solution:
    def lengthOfLIS(self, nums: [int]) -> int:
        tails, res = [0] * len(nums), 0
        for num in nums:
            i, j = 0, res
            while i < j:
                m = (i + j) // 2
                if tails[m] < num: 
                    i = m + 1           # 如果要求非严格递增，将此行 '<' 改为 '<=' 即可。
                else: 
                    j = m
            tails[i] = num
            if j == res: 
                res += 1
        return res

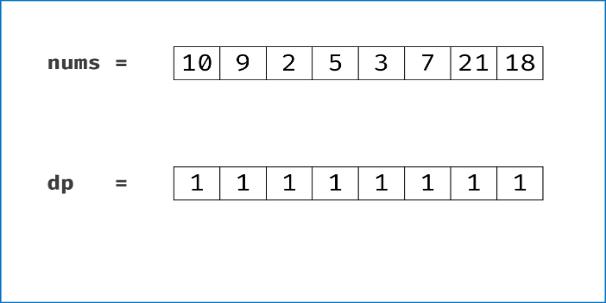
2. 动态规划

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        if not nums: return 0
        dp = [1] * len(nums)
        for i in range(len(nums)):
            for j in range(i):
                if nums[j] < nums[i]: # 如果要求非严格递增，将此行 '<' 改为 '<=' 即可。
                    dp[i] = max(dp[i], dp[j] + 1)
        return max(dp)

34. 在排序数组中查找元素的第一个和最后一个位置

        题目描述：给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target，返回 [-1, -1]。

class Solution:
    def searchRange(self, nums: List[int], target: int) -> List[int]:
        if not nums or target not in nums:          # 特例，二分查找失败
            return [-1, -1]
        return [self.lower_bound(nums, target), self.upper_bound(nums, target)]

    def upper_bound(self, nums: List[int], target: int):    # 寻找上边界
        left, right = 0, len(nums)-1
        while left <= right:
            mid = left + (right - left) // 2
            if nums[mid] <= target:     # 移动左指针
                left = mid + 1
            else:                       # 移动右指针
                right = mid -1
        return right


    def lower_bound(self, nums: List[int], target: int):    # 寻找下边界
        left, right = 0, len(nums)-1
        while left <= right:
            mid = left + (right - left) // 2
            if nums[mid] >= target:         # 当nums[mid]大于等于目标值时，继续在左区间检索，找到第一个数
                right = mid - 1
            else:           # nums[mid]小于目标值时，则在右区间继续检索，找到第一个等于目标值的数
                left = mid + 1
        return left

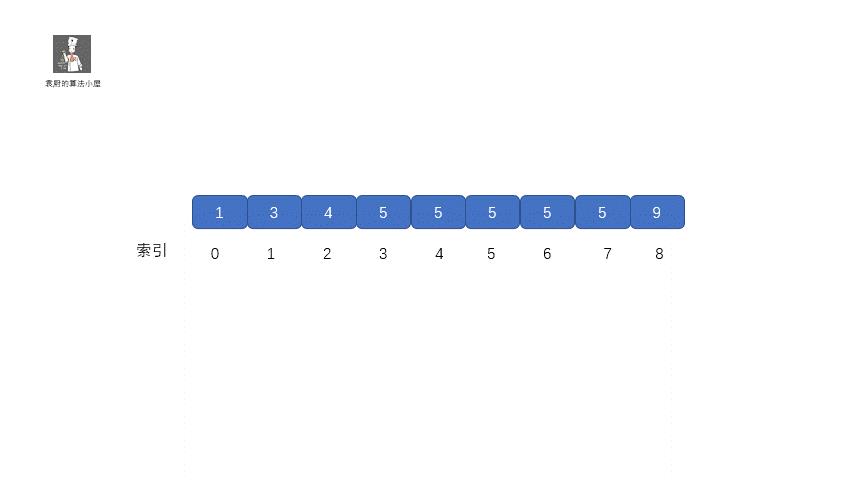
611. 有效三角形的个数
        题目描述：给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

        将数组 nums 进行升序排序，随后使用二重循环枚举 a 和 b。设 a = n u m s [ i ] , b = n u m s [ j ] a=nums[i], b=nums[j] a=nums[i],b=nums[j]，为了防止重复统计答案，我们需要保证 i < j i<j i<j。剩余的边 c 需要满足 c < n u m s [ i ] + n u m s [ j ] c<nums[i]+nums[j] c<nums[i]+nums[j]，我们可以在 [ j + 1 , n − 1 ] [j+1,n−1] [j+1,n−1] 的下标范围内使用二分查找（其中 n n n 是数组 nums 的长度），找出最大的满足 n u m s [ k ] < n u m s [ i ] + n u m s [ j ] nums[k]<nums[i]+nums[j] nums[k]<nums[i]+nums[j] 的下标 k k k，这样一来，在 [ j + 1 , k ] [j+1, k] [j+1,k]以上是关于Python数据结构与算法篇-- 二分查找与二分答案的主要内容，如果未能解决你的问题，请参考以下文章

Python数据结构与算法（19）---二分查找

Python数据结构与算法（19）---二分查找

Python数据结构与算法（19）---二分查找

python数据结构与算法第十四天二分查找

在路上---学习篇Python 数据结构和算法 二分查找二叉树遍历

Java八股文面试题 基础篇 -- 二分查找算法冒泡排序选择排序插入排序希尔排序快速排序