树二叉树堆
Posted 勤奋的懒羊羊~
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了树二叉树堆相关的知识,希望对你有一定的参考价值。
目录
一、树的表示
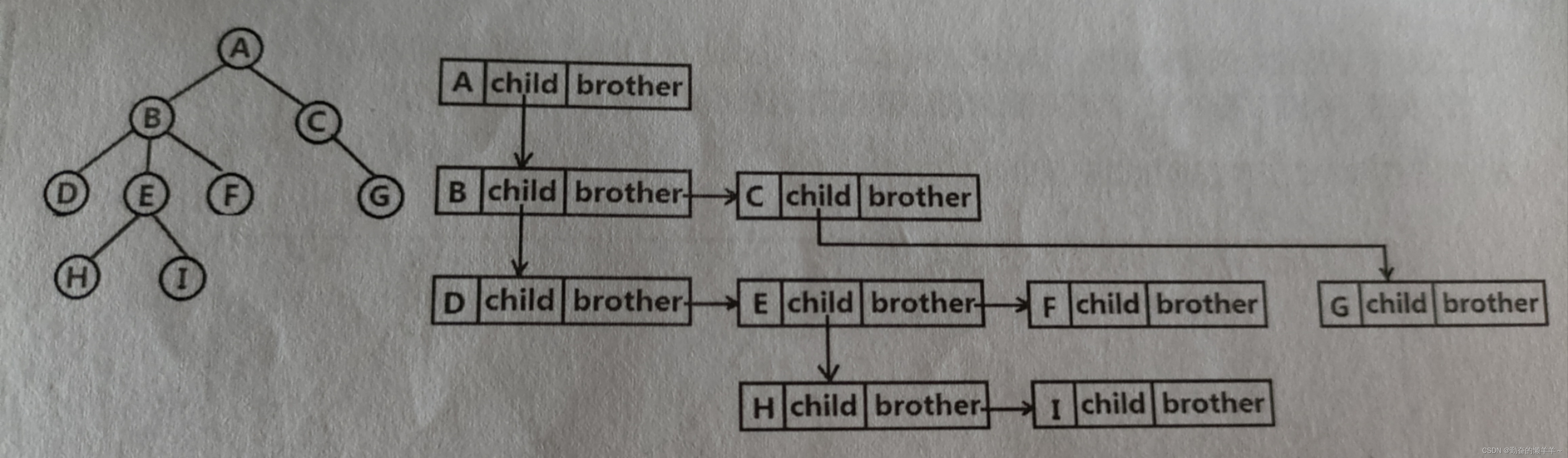
常用:孩子兄弟表示法
typedef int DataType
struct Node
struct Node*_firstchildren1;//第一个孩子结点
struct Node*_pNextBrother;//指向下一个兄弟结点
DataType _data;//结点中的数据域
;
二、二叉树的概念及结构
1、概念:
一颗二叉树是结点的一个有限集合,该集合:
1)为空
2)由一个根节点加上左子树和右子树的二叉树组成。
注意:二叉树子树有左右之分,次序不能颠倒,因此二叉树是有序树。
2、特殊的二叉树
1)满二叉树:每一层的结点数都达到最大值。如果层数为k,则该满二叉树的结点总数为2^k-1
2)完全二叉树:最后一层可以不满,但必须从左到右连续。
如果满二叉树的高度为h,则它的结点数为2^h-1
反之,如果满二叉树的结点有N个,则它的高度h为logN+1,可以看成logN。
高度为h的完全二叉树的结点数量范围是【2^(h-1),2^h-1】
对于任意一棵二叉树,度为0的永远比度为2的多一个。(每增加一个度为2的,就会增加一个度为0的)
3、二叉树的存储结构
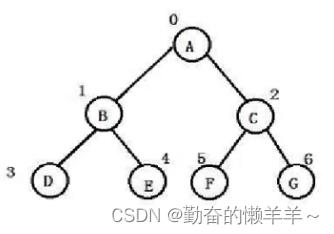
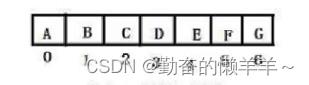
父子下标关系:
parent=(child-1)/2
child左=parent*2+1
child右=parent*2+2
但是,当二叉树不是满二叉树或完全二叉树时,会浪费空间,不适合用数组存储表示二叉树。
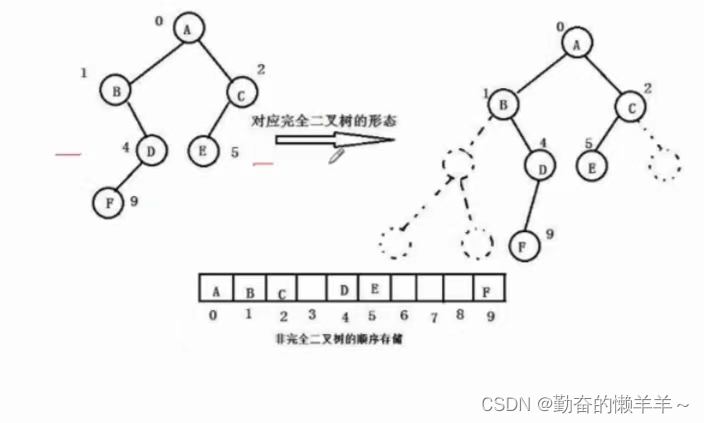
三、堆
1、大\\小根堆
小根堆:堆中某个结点总是不小于其父结点。
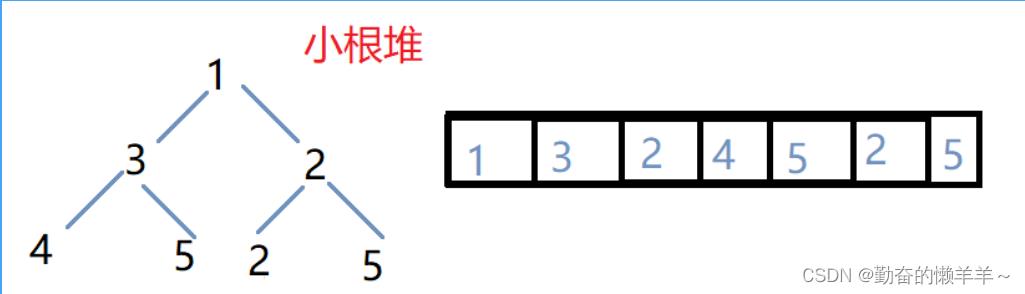
大根堆:堆中某个结点总是不大于其父结点。

堆一定是完全二叉树。
2、堆的实现
1)结构及初始化
typedef int HPDataType;
typedef struct Heap
HPDataType* a;
int size;
int capacity;
HP;
void HeapInit(HP* php)
assert(php);
php->a = (HPDataType*)malloc(sizeof(HPDataType) * 4);
if (php->a == NULL)
perror("malloc failed");
return;
php->size = 0;
php->capacity = 4;
2)插入
插入数据的关键是在数组中插入数据后调整数据位置,这里我们实现的是大堆,所以当孩子大于父亲的时候,就应该交换位置。
void HeapPush(HP* php, HPDataType x)
assert(php);
if (php->capacity == php->size)
HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity * 2);
if (tmp == NULL)
perror("realloc failed");
return;
php->a = tmp;
php->capacity *= 2;
php->a[php->size] = x;//size就是最后一个数据的下一个数据的下标
php->size++;
AdjustUp(php->a,php->size-1);
void AdjustUp(HPDataType* a, int child)
int parent = (child - 1) / 2;
while (child > 0)
if (a[child] > a[parent])
Swap(&a[child], &a[parent]);
child = parent;
parent = (child - 1) / 2;
else
break;
void Swap(HPDataType* p1, HPDataType* p2)
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
3)删除
要删除堆顶的数据,可以让顶数据与最后一个数据先交换位置,再向下调整顶数据的位置
如果它小于它的较大孩子,就让他们换位置
void HeapPop(HP* php)//删堆顶
assert(php);
assert(!HeapEmpty(php));
Swap(&php->a[php->size-1], &php->a[0]);
php->size--;
AdjustDown(php->a,php->size,0);
void AdjustDown(HPDataType*a,int n,int parent)
int child = parent * 2 + 1;
while (child < n)
//选出左右孩子中大的那一个
//a[child + 1] > a[child] && child + 1 < n 不能这样写!
//a[child + 1]已经越界访问了
if (child + 1 < n && a[child + 1] > a[child])
child++;
if (a[child] > a[parent])
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
else
break;
4)取堆顶数据
HPDataType HeapTop(HP* php)
assert(php);
return php->a[0];
5)判空
bool HeapEmpty(HP* php)
assert(php);
return php->size == 0;
6)大小
int HeapSize(HP* php)
assert(php);
return php->size;
7)销毁
void HeapDestroy(HP* php)
assert(php);
free(php->a);
free(php);
四、堆排序
要想利用堆来给一组数排序
第一步:建堆(利用堆插入数据的过程,一个个插入)
第二步:排升序,建大堆;排降序,建小堆。
以排升序为例:

end一开始指向3, 当3和20互换且3的位置调整好后,20的位置就定下来了,
如何再让end=end-1,此时end指向5,再让5与第一个数交换调整……
void HeapSort(int* a,int n)
//向上调整建堆
for (int i = 0; i < n; i++)
AdjustUp(a, i);
int end = n - 1;
while (end > 0)
Swap(&a[end], &a[0]);
AdjustDown(a, end, 0);
end--;
扩展:建堆也可以用向下调整建堆

以上是关于树二叉树堆的主要内容,如果未能解决你的问题,请参考以下文章