什么叫中国剩余定理

Posted 2023-03-25

中国剩余定理释义：又称“孙子定理”。1852年，英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲。1874年，英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理，因而西方称之为“中国剩余定理”。

孙子定理是中国古代求解一次同余式组（见同余）的方法。是数论中一个重要定理。又称中国余数定理。一元线性同余方程组问题最早可见于中国南北朝时期（公元5世纪）的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”问题，原文如下：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。《孙子算经》中首次提到了同余方程组问题，以及以上具体问题的解法，因此在中文数学文献中也会将中国剩余定理称为孙子定理。

扩展资料：

中国剩余定理说明：假设整数m1,m2, ... ,mn两两互质，则对任意的整数：a1,a2, ... ,an，方程组  有解，并且通解可以用如下方式构造得到：设 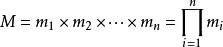 是整数m1,m2, ... ,mn的乘积，并设  是除了mi以外的n- 1个整数的乘积。

方程组  的通解形式为 

一元线性同余方程组问题最早可见于中国南北朝时期（公元5世纪）的数学著作《孙子算经》卷下第二十六题，叫做“物不知数”问题，原文如下：

有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？

即，一个整数除以三余二，除以五余三，除以七余二，求这个整数。《孙子算经》中首次提到了同余方程组问题，以及以上具体问题的解法，因此在中文数学文献中也会将中国剩余定理称为孙子定理。

宋朝数学家秦九韶于1247年《数书九章》卷一、二《大衍类》对“物不知数”问题做出了完整系统的解答。明朝数学家程大位将解法编成易于上口的《孙子歌诀》：

三人同行七十稀，五树梅花廿一支，七子团圆正半月，除百零五使得知

这个歌诀给出了模数为3、5、7时候的同余方程的秦九韶解法。意思是：将除以3得到的余数乘以70，将除以5得到的余数乘以21，将除以7得到的余数乘以15，全部加起来后减去105（或者105的倍数），得到的余数就是答案。比如说在以上的物不知数问题里面，按歌诀求出的结果就是23。

参考资料：百度百科---孙子定理

参考技术A 如果正整数m1、m2、……、mk两两互质，那么同余方程组
x≡a,(mod mi), i=1,2,……k 有无穷多解。 且这些解关于模 M=m1,m2,……，mk同余，可表成
x≡a1,M'1M1+a2M'2M2+……+akM'KMK(mod M).
其中Mk=M/m,而M'k是满足M'kMk=1(mod mk)的正整数。这一算法后来传入西方，被称为中国剩余定理。

注：互质，也称互素。即两个数的最大公约数(最大公共因数，great common divisor)为1, 记号：gcd(a,b)=1.

名题：
三三数之剩二，置一百四十，五五数之剩三，置六十三，七七数之剩二，置三十，并之，得二百三十三，以二百一十减之，即得。凡三三数之剩一，则置七十，五五数之剩一，则置二十一，七七数之剩一，则置十五，即得。
即：
1、将军点兵，三三数余2，五五数余3，七七数余2。问兵几何？
2、今有物不知其数,三三数之剩二,五五数之剩三,七七数之剩二,问物几何?——《孙子算经》
由于孙子算经成书较早，并且较早地介绍了这样的问题，故中国剩余定理的众多异名中，一个著名的另名是：孙子定理。

写成数论记号：同余号≡以下简记为==
x==2 mod 3
==3 mod 5
==2 mod 7
这在数论中称为同余方程组，简称同余式组。

中国剩余定理就是求解同余式组的手段之一(注意，并不是唯一方法)。它的思想是这样的：
求出
x1==1 mod 3
==0 mod 5
==0 mod 7
x2==0 mod 3
==1 mod 5
==0 mod 7
x3==0 mod 3
==0 mod 5
==1 mod 7
那么2x1+3x2+2x3即为所求解x。

如果用向量记法，就更容易理解：
原题：x==(2,3,2) mod (3,5,7)
孙子定理：x1==(1,0,0);x2==(0,1,0);x3=(0,0,1)
x==2x1+3x2+2x3.

在求解x1时，显然x1==(0,0)mod (5,7),即x1被5，7整除。从而可设x1=5*7*k1==1 mod 3.
这里k1就是人们所说的乘率，古人求k1常用的就是大衍求一术。

这种方法实际上就是分化了维度，通过单位向量简化问题。近世代数的许多观点与方法，与这不谋而合，实际是受了中国剩余定理的启发。还有拉格朗日插值法，也与此一致。

同时我们还可以看到，x==(2,3,2) mod (3,5,7)
还可以等效于x==(2,2,2)+(0,1,0)，这样无疑是对上述算法的一种改进。正如牛顿插值法相对于拉格朗晶插值的改进。

以上内容，来自wsktuuytyh (用户名来源于姓名的五笔编码：wsk 何 tuu 冬 ytyh 州)的百度答题与博文。欢迎引用。欢迎交流。本回答被提问者和网友采纳 参考技术B

中国剩余定理（孙子定理）不足表现

中国剩余定理（孙子定理）不足表现