疯狂Java——树和二叉树（第11章）

Posted 2020-10-04

树代表一种非线性的数据结构。

术语：

叶子节点：没有子节点的节点，因此叶子节点不可作为父节点；

节点的度：节点拥有的子树的个数被称为该节点的度（degree）;

树的度：树中所有节点的度的最大值就是该树的度；

节点层次：节点的层次从根开始算起，根的层次值为1，其余节点的层次值为父节点层次值加1；

树的深度（depth）：树中节点的最大层次值称为树的深度或高度；

有序树与无序树:如果将树中节点的各个子树看成从左到右是有序的（即不能互换），则称该树为有序树，否则称为无序树。

父亲点表示法：每个子节点都记录它的父节点；(这种方式是从子节点着手)

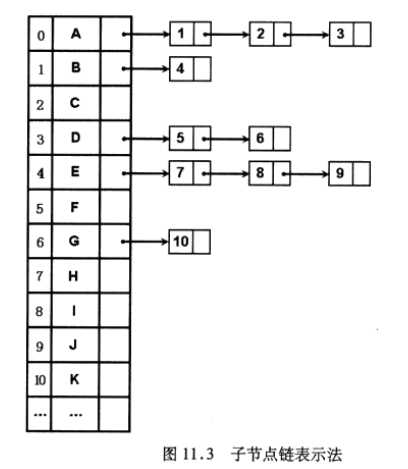
孩子链表示法：每个非叶子节点通过一个链表来记录它所有的子节点。（这种方式是从父节点着手，特点：每个节点都可以快速找到它的所有子节点）如下图：

二叉树:每个节点最多只有两个子树的有序树。

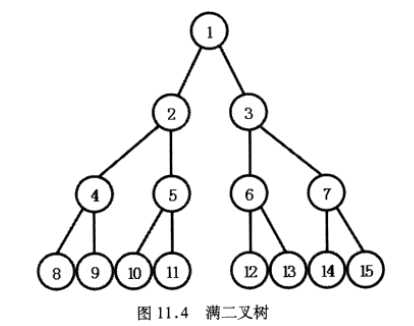
满二叉树：如果一棵二叉树的深度为k,则其包含2^k-1个节点。满二叉树如下图：

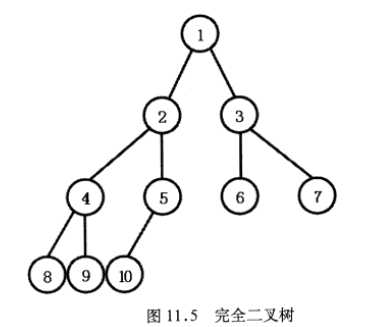
完全二叉树：一棵有n个节点的二叉树，按满二叉树的编号方式对他进行编号，若树中所有节点和满二叉树1-n编号完全一致，则称该树为完全二叉树。也就是说除最后一层外，其余层的所有节点都是满的。如下图：

 

 二叉树性质：

1）在任何一棵二叉树中，如果其叶子节点的数量为N₀,度为2的子节点数量为N₁，则N₀=N₁+1;

2)具有N个节点的完全二叉树的深度为log₂^N+1;

二叉树的二叉链表存储的思想：让每个节点都能记住它的左、右两个节点。为每个节点增加left、right两个指针，分别引用该节点的左、右两个子节点。

二叉树的三叉链表存储的思想：让每个节点不仅记住它的左右节点，还能记住它的父节点，利用指针parent。

遍历二叉树

I、先序遍历：

    1）访问根节点；

    2）递归遍历左子树；

    3）递归遍历右子树；

II、中序遍历：

    1）递归遍历左子树；

    2）访问根节点；

    3）递归遍历右子树；

III、后序遍历：

         1）递归遍历右子树；

    2）访问根节点；

    3）递归遍历左子树；

广度优先遍历：按层遍历；