OpenCV——图像灰度变换

Posted 心无旁骛~

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了OpenCV——图像灰度变换相关的知识，希望对你有一定的参考价值。

文章目录

图像灰度变化

灰度变换介绍

  • 由于外部环境光照影响，或由于成像设备的非线性和图像记录设备动态范围太窄等，
    获取到的图像可能不够理想，细节分辨不清，即对比度不足。
  • 简单来说，对比度是最白与最黑亮度单位的比值。白色越亮、黑色越暗，则对比度就越高。
  • 可以使用灰度变换方法解决对比度不足的问题。


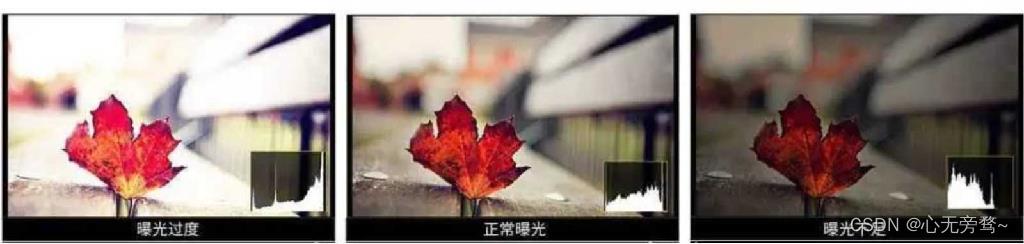
曝光过度的照片整体过亮，曝光不足的照片整体过暗。这两种情况下图片里的物体都缺乏细节辨识度。

灰度变换是将输入图像中的每个像素 f ( x , y ) f(x, y) f(x,y)通过映射函数 T T T变换成输出图像中的灰度值 g ( x , y ) g(x, y) g(x,y)。
g ( x ， y ) = T [ f ( x ， y ) ] g(x，y)=T[f(x，y)] g(x，y)=T[f(x，y)]

根据变换函数的性质不同，灰度变换可以分为：

  • 灰度线性变换
  • 灰度分段线性变换
  • 灰度非线性变换

灰度线性变换

  • 采用线性函数对图像的每一个像素作线性扩展，扩展图像的动态范围。
  • 对图像作灰度线性或分段线性变换，扩大图像的对比度，将有效地改善图像视觉效果。

设原图像灰度取值 f ( x , y ) ∈ [ a , b ] f(x,y)\\in[a,b] f(x,y)∈[a,b]，线性变换后的图像灰度取值 g ( x , y ) ∈ [ c , d ] g(x,y)\\in[c,d] g(x,y)∈[c,d] 则灰度线性变换为：
g ( x , y ) = k [ f ( x , y ) − a ] + c g(x,y)=k[f(x,y)-a]+c g(x,y)=k[f(x,y)−a]+c


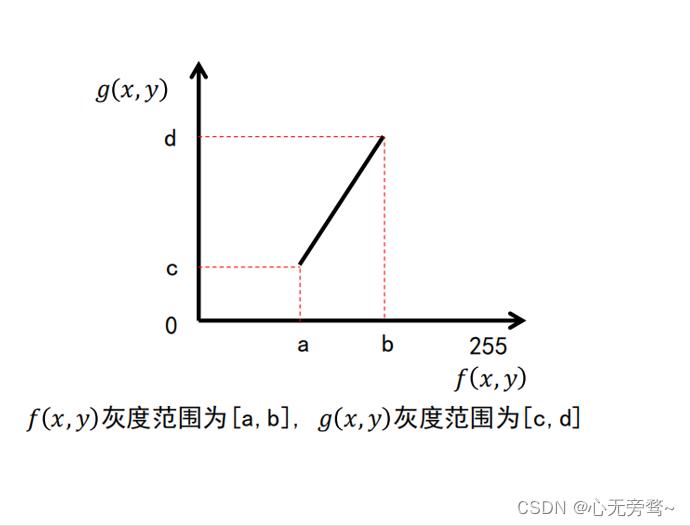
式子中， k = d − c b − a k=\\fracd-cb-a k=b−ad−c​为线性变换函数（直线）的斜率。

  • 扩展动态范围， k > 1 k>1 k>1
  • 缩小动态范围， 0 < k < 1 0<k<1 0<k<1

灰度线性变化示例：

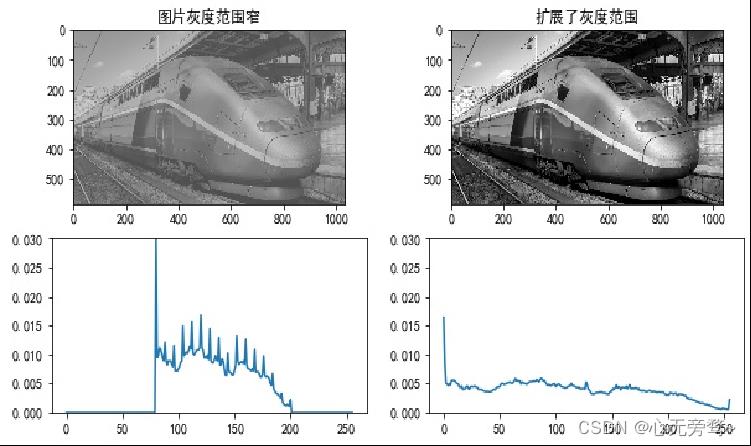
当 k = 1 k=1 k=1的时候，就变为加常数线性变换 g ( x , y ) = f ( x , y ) + c g(x,y)=f(x,y)+c g(x,y)=f(x,y)+c，可以压缩动态范围，降低对比度。

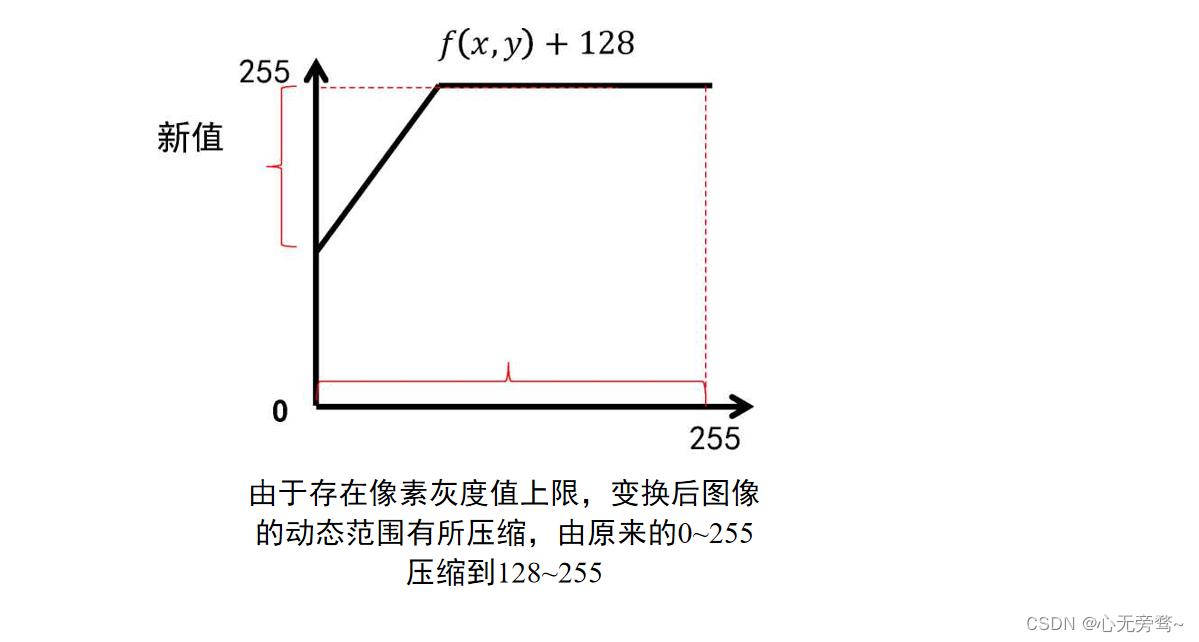
加常数线性变换实例：

灰度分段线性变换

灰度线性变换的缺点：
不够灵活，将原始图像中的灰度值不加区别的扩展。

在实际应用中：

  • 为了突出图像中感兴趣的研究对象，常常需要局部扩展某一范围的灰度值；
  • 对不同范围的灰度值进行不同程度的扩展。

举例：
设图像的整个灰度范围比较宽，为[0, M]，但感兴趣的某两个灰度值之间的动态范围较窄，为[a, b]。采用灰度分段线性变换来扩展感兴趣的[a, b]区间。具体情况有两种，对应的变换关系如下图所示。其中，图(a)是“扩展感兴趣区域，牺牲其他区域”处理的函数图形示例，图(b)是“扩展感兴趣区域，压缩其他区域”处理的函数图形示例。

灰度分段线性变换实例：

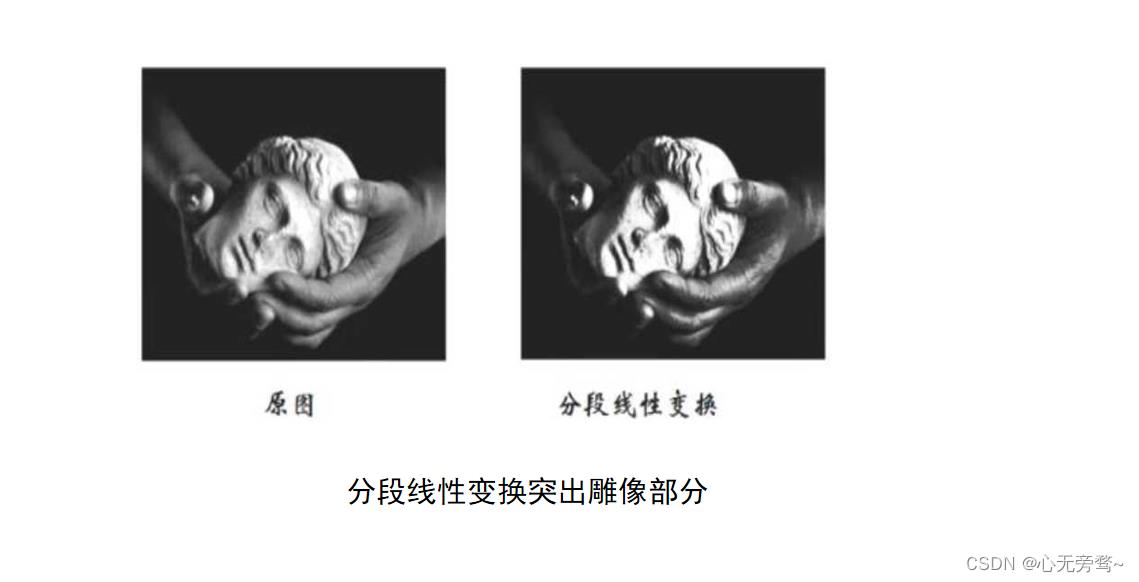
图像点运算

定义：

对图像中的每个像素进行灰度变换运算。
输出图象每个象素点的灰度值仅由输入图像相同位置象素点的灰度值决定。

设输入图像和输出图像在 ( x , y ) (x,y) (x,y)处的灰度值分别是 r r r 和 s s s，则点运算可表示为 s = T ( r ) s = T(r) s=T(r), T T T 表示输入图像与输出图像像素的灰度映射关系。

运算的用途：实现对比度增强等。

图像的点运算包括：

  • 灰度变换
    • 线性变换
    • 非线性变换(对数变换、伽马变换、阈值变换，分段线性变换等)
  • 位图切割

灰度非线性变换

非线性变换定义：

  • 对于 g ( x , y ) = T [ f ( x , y ) ] g(x,y)=T[f(x,y)] g(x,y)=T[f(x,y)]，如果 T [ ⋅ ] T[·] T[⋅]是非线性变换函数，那么该变换为非线性变换。
  • 常用的非线性变换有对数变换、幂次变换（伽马变换）等。

线性点运算

输出输入的灰度值成线性函数关系： s = f ( r ) = a r + b s =f(r)=ar+b s=f(r)=ar+b

  • a a a 控制对比度(不同级别灰度的明暗差异)：
    • a > 1，对比度变大；
    • a < 1，对比度变小。
    • a 为负值，实现负片效果
  • b b b 控制输出图像的整体亮度：
    • b > 0 增大亮度
    • b < 0 则减小亮度
import cv2 as cv

# 线性变换
def linear(img,a,b):
    """
    s =f(r)=ar+b
    """
    r = np.copy(img)
    s = a*r+b
    return s
if __name__=="__main__":
    img = cv.imread("3.png")
    img = cv.cvtColor(img,cv.COLOR_RGB2GRAY)
    # 调节 a,b值观察图像变化
    a = 1
    b = 255
    re_img = linear(img,a,b)
    cv.imshow('img',img)
    cv.imshow('re_img,a=,b='.format(a,b),re_img)
    cv.waitKey(0)
    cv.destroyAllWindows()


灰度的线性变换不利于突出感兴趣区域，且容易出现饱和、截止等情况。

灰度的非线性变换：对数变换

灰度的线性变换不利于突出感兴趣区域，且容易出现饱和、截止等情况。有时原图含有较多的暗部区域，某些显示设备呈现低灰度的能力有限，如果直接使用原图，则一部分细节可能丢失。

解决办法：进行非线性变换,即对原图进行对数变换，增强暗部区域的对比度。

对数变换的一般表达式为：
g ( x , y ) = λ l g [ f ( x , y ) + 1 ] \\mathbfg(x,y)=\\lambda lg[f(x,y)+1] g(x,y)=λlg[f(x,y)+1]

式中， λ λ λ为尺度比例系数，用来调节变换后的灰度值的动态范围，使其更符合实际需要。对数变换可以扩展图像的低灰度值范围，同时压缩高灰度值范围，使图像灰度值分布均匀，更加匹配人的视觉特性，示例图如下图所示。

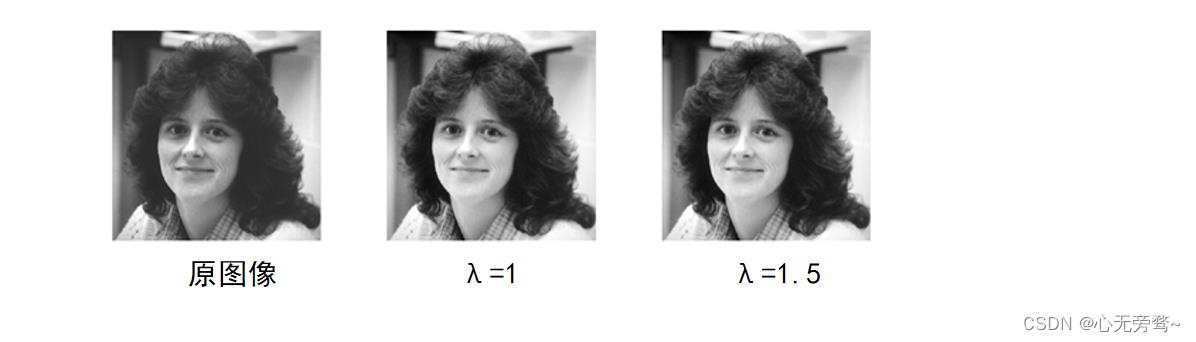
对数变换尤其适用于灰度范围特别大的情况。
例：傅里叶频谱的灰度范围可能超过8位灰度图像的范围,例如

附：

灰度对数变换(可增强暗部细节)： s = c l o g ( 1 + r )   c 为常数，建议值 c = 255 / l o g ( 256 ) s = clog(1+r)\\ c为常数，建议值c = 255/log(256) s=clog(1+r) c为常数，建议值c=255/log(256)
灰度反对数变换(可增强亮部细节)： s = e x p ( r / c ) − 1 s = exp(r/c) - 1 s=exp(r/c)−1

灰度的非线性变换：伽马变换

伽玛变换又称为 指数变换 或 幂次变换，是另一种常用的灰度非线性变换。
网上大多数给的指数函数的基本形式为： s = c r γ   c ≥ 0 , γ ≥ 0 ; s = cr^\\gamma \\ c\\geq0,\\gamma\\geq0; s=crγ c≥0,γ≥0;
实际使用公式: s = 255 × ( r 255 + e p s ) γ s = 255\\times(\\fracr255+eps)^\\gamma s=255×(255+epsr​)γ

e p s eps eps 为补偿系数（一般为0）， γ \\gamma γ 为伽马系数
当 γ < 1 \\gamma<1 γ<1 时，低亮度区域对比度增强
当 γ > 1 \\gamma>1 γ>1 时， 高亮度区域对比度增强
当 γ = 1 \\gamma=1 γ=1时，该灰度变换是线性的，此时通过线性方式改变原图像。

这里给出更加详细的一般表达式： g ( x , y ) = λ [ f ( x , y ) + ξ ] γ g(x,y)=\\lambda[f(x,y)+\\xi]^\\gamma g(x,y)=λ[f(x,y)+ξ]γ

式中，参数 λ λ λ为常数，可以改变指数变换曲线的变换速率。参数 ε ε ε为常数，可以改变指数变换曲线的起始位置。参数 γ γ γ也为常数，其取值对变换函数的特性有很大的影响。
指数变换函数曲线如下图所示。

  • 图(a)表示 γ < 1 γ<1 γ<1时的指数变换函数曲线。当 γ < 1 γ<1 γ<1时，指数变换的作用与对数变换类似，输入的高灰度范围被压缩，低灰度范围被拉伸，实现了强化暗部压缩亮部的图像增强效果。
  • 图(b)表示 γ > 1 γ>1 γ>1时的指数变换函数曲线。当 γ > 1 γ>1 γ>1时，输入的低灰度范围被压缩，高灰度范围被拉伸，实现了强化亮部压缩暗部的图像增强效果。

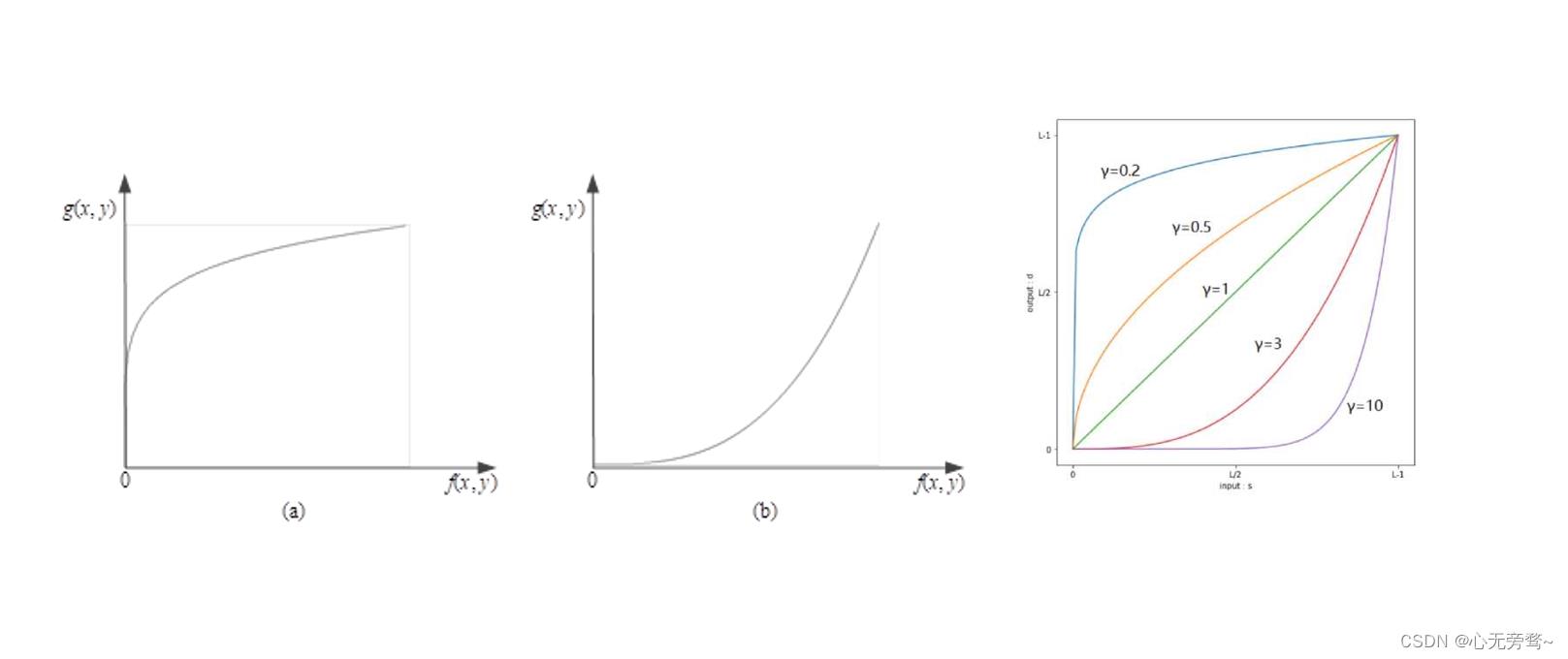
不同 γ \\gamma γ值的变换曲线如下图所示：

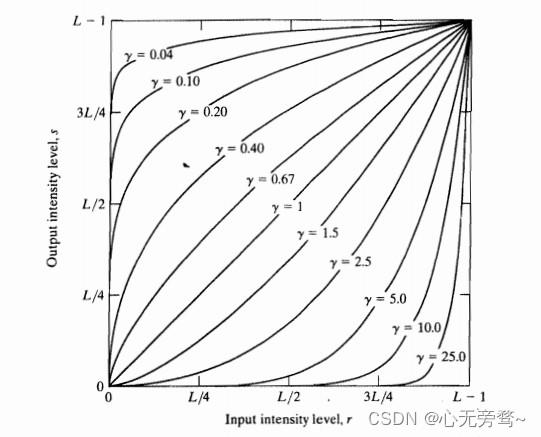
指数变换拉大了不同点的灰度值距离，提高了图像的对比度。对图像采用不同 γ γ γ值的指
数变换结果如下图所示。其中，图(a)是原图像，图(b)是 γ = 0.6 γ=0.6 γ=0.6时的指数变换的结果，
图©是 γ = 1.7 γ=1.7 γ=1.7时的指数变换的结果。

附代码实现：

# 非线性变化：γ变换
def gamma(img,gamma):
    """
    s = c * r^gamma
    """
    r = np.copy(img)
    s = np.power(r/255,gamma)

    return s


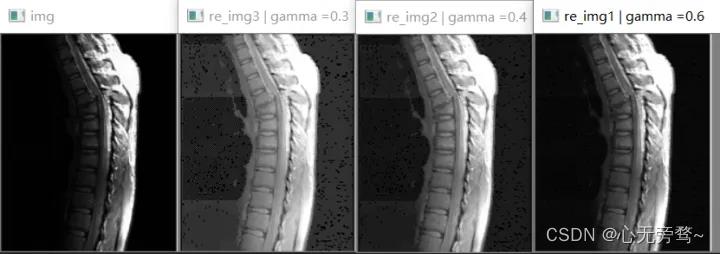
分段线性变换和伽马变换例子：

#1、导入包
import cv2
import numpy as np
import math
import matplotlib.pyplot as plt


#2、读入图片
gray_img = cv2.imread('spine.tif',0)
cv2.imshow('gray_img',gray_img)
cv2.waitKey(0)
cv2.destroyAllWindows()

#3、构造跟原图同样大小的零值图，用于保存分段线性变换结果
piecewise_linear_img = np.zeros((gray_img.shape[0],gray_img.shape[1]),np.uint8)

#4、设置分段线性函数参数
r1,s1 = 40,100
r2,s2 = 200,250
k1 = s1/r1
k2 = (s2-s1)/(r2-r1)
k3 = (255-s2)/(255-r2)

#5、便利图像每个像素，按公式进行变换
for i in range(gray_img.shape[0]):
    for j in range(gray_img.shapeOpenCV 完整例程39. 图像灰度的线性变换


 OpenCV 完整例程43. 图像的灰度变换（对数变换）


 OpenCV 完整例程44. 图像的灰度变换（伽马变换）


 OpenCV 完整例程40. 图像分段线性灰度变换


 OpenCV 完整例程42. 图像的灰度变换（比特平面分层）


 OpenCV图像增强---灰度变换直方图均衡化