KDD2016-Structural Deep Network Embedding

Posted 2023-03-15 吾仄lo咚锵

文章目录

• 介绍
• SDNE
• • 问题定义
  • 框架
  • 损失函数
• 实验
• • 数据集和超参
  • 图重建
  • 多标签分类
  • 链路预测
  • 可视化
  • 参数敏感性
• 总结

前些天发现了一个巨牛的人工智能学习网站，通俗易懂，风趣幽默，忍不住分享一下给大家。点击跳转到网站。

介绍

---

Wang D, Cui P, Zhu W. Structural deep network embedding[C]//Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. 2016: 1225-1234.

网络无处不在，许多现实世界中的应用程序都需要挖掘网络中的信息。比如社交网络中推荐好友，在网络集群用户并推荐商品，在蛋白质网络中研究分子等，挖掘网络中的信息是非常重要的。

一个有效的方法就是将网络嵌入到一个低维空间，然后通过学习到的嵌入向量对网络进行重建，也就是用图嵌入的方法学习网络的表示。

但是学习网络表示面临着以下3个挑战：

1. 高度非线性化
   网络中的潜在结构是高度非线性的，因此设计模型来捕捉这种高度非线性的结构是很困难的。
2. 如何保留结构
   网络中潜在结构是非常复杂的，节点间的相似性依赖局部和全局网络架构，如何同时保留局部和全局结构也是一个棘手的问题。
3. 稀疏性问题
   许多真实世界的网络是高度稀疏的，仅利用非常有限的观察到的边不足以达到令人满意的性能。

对于上述三个问题，SDNE分别提出了解决方法：
设计一个深度模型来学习网络中的节点表示，包含多个非线性函数的多层架构，可以将数据映射到高度非线性的潜在空间，从而能够捕获高度非线性的网络结构。
利用一阶临近度和二阶临近度来解决如何保留结构和稀疏性问题，利用一阶临近度和二阶临近度可以分别保留局部和全局网络结构，为此同时保留二者，提出了一个半监督框架来学习表示。

此外，如图1所示，节点间的二阶临近度的数量是远远多于一阶临近度的，因此二阶临近度可以提供更多的信息来描述网络结构。

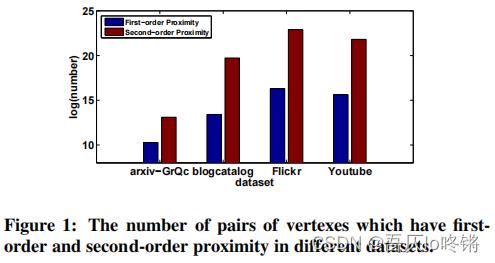
总的来说，SDNE贡献如下：

1. 一个结构化深度网络嵌入方法，称为SDNE。可以将数据映射到一个高度非线性潜在空间来保留网络结构，并且对于系数网络也具有鲁棒性。
2. 一个新的半监督深度模型，同时利用了一阶临近度和二阶临近度，来保留局部和全局网络结构。
3. 通过实验表明了SDNE的优越性。

SDNE

问题定义

---

• 图（Graph）
  定义图$G=(V,E)$，其中$V=v_1,...,v_n$表示n个节点，$E={e_{i,j}}_{i,j=1}^n$表示边，其中每条边的权重为$s_{i,j}$，若节点间不存在边则$s_{i,j}=0$；若存在边，对于无权重图$s_{i,j}=1$，对于有权重图$s_{i,j}>1$。

• 一阶临近度（First-Order Proximity）
  对于任何一对节点，若$s_{i,j}>0$则表明节点$v_i$和节点$v_j$之间存在一阶临近度，否则不存在一阶临近度。也就是看邻接矩阵中具体值，一节邻近度描述了两节点是否相连，是否存在边。

• 二阶临近度（Second-Order ）
  给定$N_u=s_{u,1},...,s_{u,|v|}$表示节点$u$和其他节点的一阶临近度，节点$u$和节点$v$间二阶临近度则是$N_u$和$N_v$的相似性。也就是比较邻接矩阵中的两行，二阶临近度描述了两节点有多少共同邻居。

• 图嵌入（Network Embedding）
  图嵌入旨在学习一个映射函数$f:v_i\to y_i\in {\mathbb{R}}^d$，其中$d<<|V|$。也就是从高维映射到低维，映射过程称为嵌入，得到映射结果为嵌入向量。

框架

---

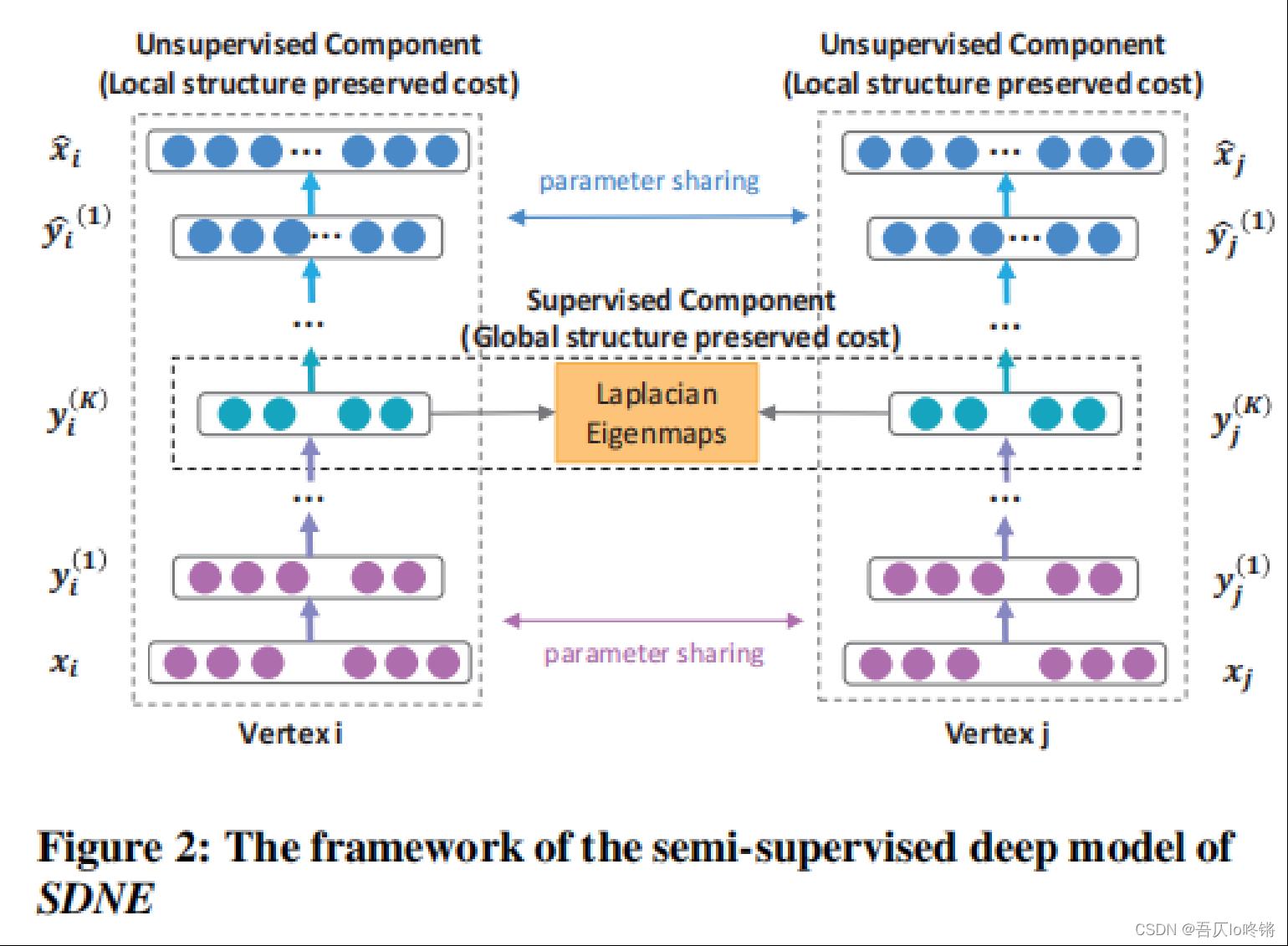
SDNE模型是一个半监督深度学习模型。

对于节点$i$的输入特征$x_i$（邻接矩阵第$i$行），经过$K$层全连接层的编码器（隐含层神经元个数递减），嵌入到一个低维空间，得到嵌入向量$y_i^{(K)}$，然后再经过$K$层的全连接层的解码器（与编码器相反且一一对应），学习到解码后节点$i$的新特征表示。自编码器中是用的非监督损失函数，最优化二阶临近度，保留全局结构特征（我怀疑图片上标错了）。

对于两个节点$i$和$j$，对拉普拉斯特征值映射进行扩展，使用监督损失函数，最优化一阶临近度，保留局部结构特征。

通过联合优化一阶邻近度和二阶临近度，同时保留图的局部和全局结构特征。下面介绍具体损失函数定义。

损失函数

---

• 一阶临近度损失
  使用一阶临近度来保留网络的局部特征，作为监督信息来约束一对顶点的潜在表示的相似性。
  $${\mathcal{L}}_{1st}=\sum _{i,j=1}^n{s}_{i,j}{||y_i-y_j||}_2^2$$
  idea源于拉普拉斯特征值映射，当相似节点在嵌入空间中映射得较远时给予惩罚。使由一条边连接的顶点映射到嵌入空间后相近。

• 二阶临近度损失
  使用二阶临近度来保留网络的全局特征，使有更多相同邻居的节点映射到嵌入空间后更相近。但是直接使用邻接矩阵作为传统自编码器的输入，将更倾向于重建邻接矩阵中的零元素。而这并不是我们所期待的，因此提高了重建非零元素的惩罚权重，如下所示：
  $${\mathcal{L}}_{2nd}={||(\hat{X}-X)\odot B||}_F^2$$
  其中，$b_i={b_{i,j}}_{j=1}^n$，当$s_{i,j}=0,b_{i,j}=1$，否则$b_{i,j}=\beta >1$。也就是重建非零元素的权重$\beta >1$大于重建零元素的权重，避免学习到全是0矩阵，以及稀疏矩阵数据不平衡情况。换句话说，如果一个数据集是全连接的话就不需要$B$了。

• 正则化损失
  预防过拟合的情况。
  $${\mathcal{L}}_{reg}=\frac{1}{2}\sum _{k=1}^K(||W^{(k)以上是关于KDD2016-Structural\; Deep\; Network\; Embedding的主要内容，如果未能解决你的问题，请参考以下文章}$$

  文献总结SDNE：Structural Deep Network Embedding

  应用在大规模推荐系统，Facebook提出组合embedding方法 | KDD 2020

  使用 n-deep 包装器类型堆栈获取模式

  N皇后问题

  reinforcement learning和deep learning的区别

  Deep learning网络调参技巧